Колчанова Г.Р.
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательский проект по математике Использование теории принятия решений на практике (9 класс)
Содержание
- 1. Исследовательский проект по математике Использование теории принятия решений на практике (9 класс)
- 2. Теория принятия решенийАктуальностьКаждый человек должен уметь принимать решения и понимать их возможные последствия.
- 3. Теория принятия решенийГипотезаИспользуя теорию принятия решений на практике, можно успешно достигать свои жизненные цели.
- 4. Теория принятия решенийЦель:Доказать важность умения принимать оптимальное
- 5. Теория принятия решенийЗадачи:Выяснить какие математические методы и
- 6. Лагранж Жозеф Луи(25.I.1736 — 10.IV.1813)французский математик и механик
- 7. Методы «Теории принятия решений» используют в самых различных областях управления.
- 8. Задачи теории расписанийГрафики движения поездов, ремонт составов
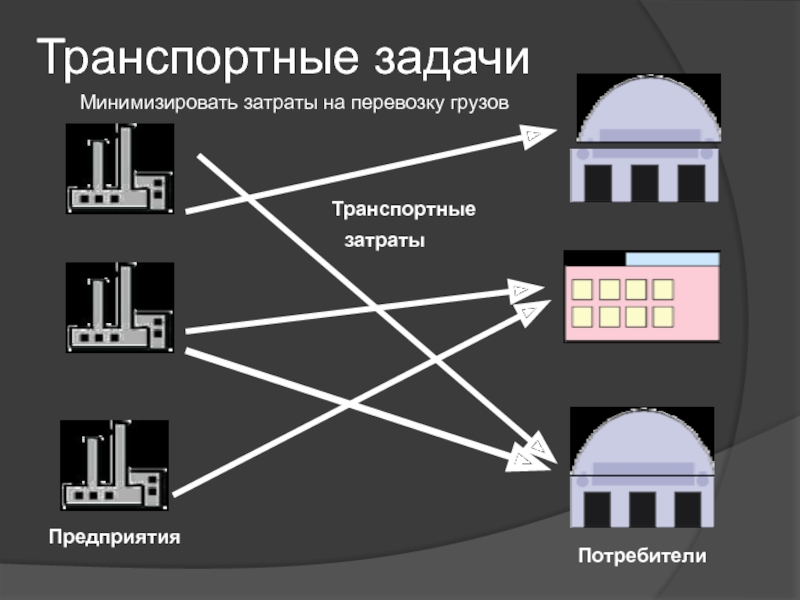
- 9. Транспортные задачиПредприятия Потребители Транспортные затраты Минимизировать затраты на перевозку грузов
- 10. Задачи размещения производстваСистемы сотовой связи, филиалы банков, производство продукции
- 11. Задачи раскроя и упаковкиРаскрой пиломатериала, листового железа
- 12. Задачи маршрутизацииНайти маршрут минимальной длины
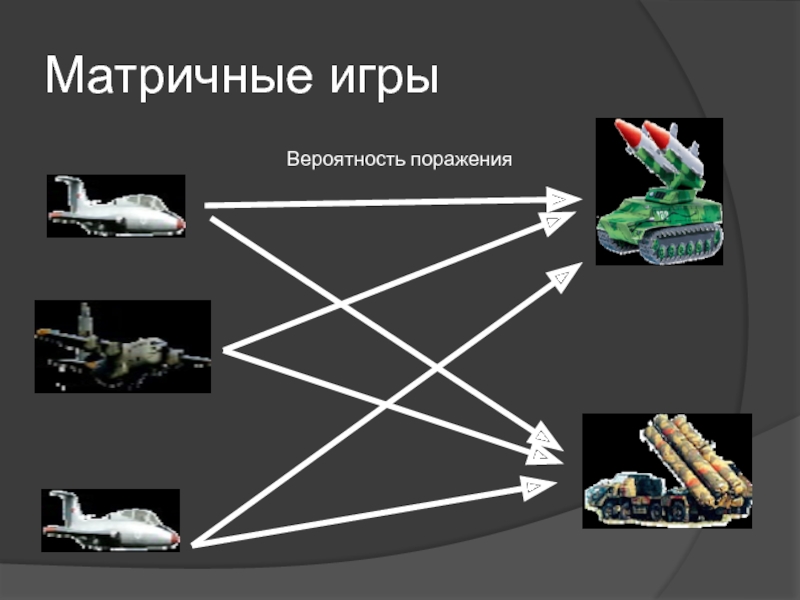
- 13. Матричные игры Вероятность поражения
- 14. Методы принятия решений1. Решение задачи с помощью
- 15. Метод поэтапного сравнения Некоторая фирма решает
- 16. 28 вопросов-сравнений 1. Будет ли предложение А
- 17. Ответы на вопросы оформим в виде таблицы, где математический знак > здесь означает «важнее чем».
- 18. Слайд 18
- 19. В ходе сравнения свои значения поменяли величины
- 20. Решение задачи с помощью построения дерева решений.
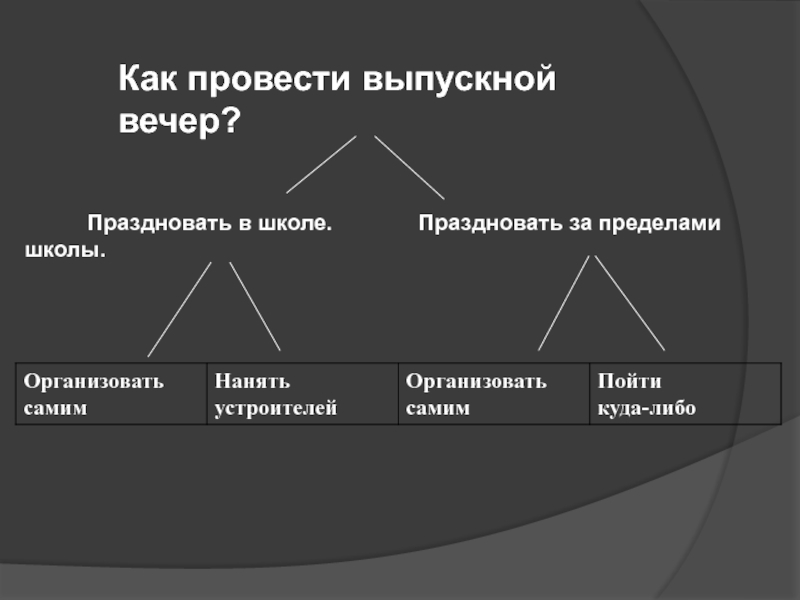
- 21. Как провести выпускной вечер?
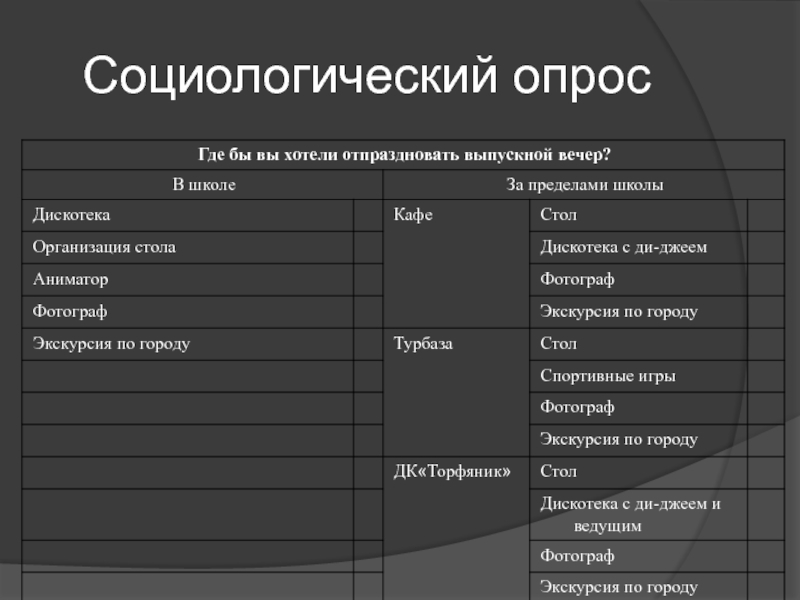
- 22. Социологический опрос
- 23. Дерево решенийВыпускной вечер, 35 чВ школе, 5чЗа
- 24. Анализ результатов По данным результатам можно
- 25. Бинарные решающие матрицыБинарные решающие матрицы представляют собой
- 26. 1.Canon Ixus 750 (A) 2.Nikon Coolpix S1
- 27. Критерии оценивания1.Габариты, вес2.Зум3.Дисплей4.Память5.Питание6.Наличие русифицированного меню7.Разрешение снимков8.Условия гарантии
- 28. Таблица оцениванияЗатем я посчитала суммы: наименьшая обнаружилась
- 29. Таблицы оценокВ таблице оценок различные варианты решений,
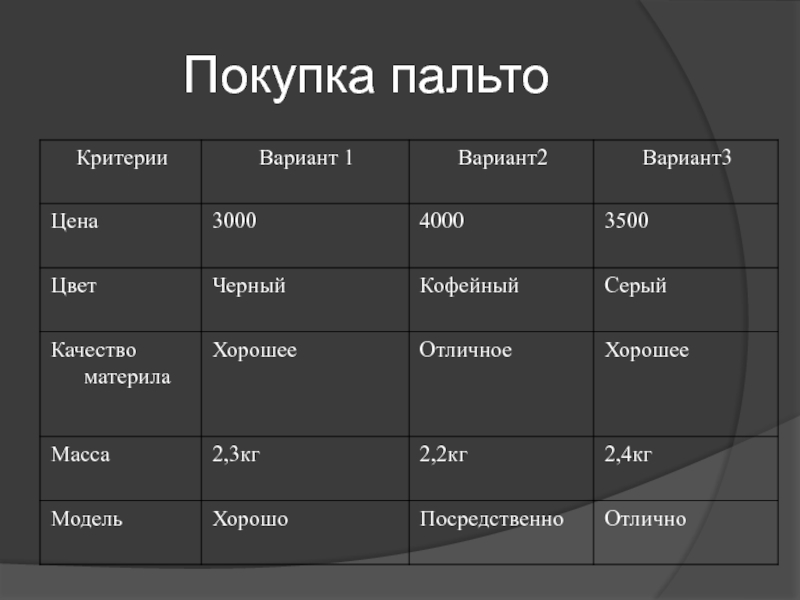
- 30. Критерии1.Цена.2.Цвет3.Качество материала4.Масса5.Модель
- 31. Покупка пальто
- 32. Весовой коэффициент
- 33. Таблица оценокИсходя из таблицы оценок, можно сделать
- 34. ВыводНа примере рассмотренных задач становится ясно насколько
Теория принятия решенийАктуальностьКаждый человек должен уметь принимать решения и понимать их возможные последствия.
Слайд 1ИСПОЛЬЗОВАНИЕ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ НА ПРАКТИКЕ
Выполнила: Райм Наталья, ученицы 9А класса
Руководитель:
Слайд 2Теория принятия решений
Актуальность
Каждый человек должен уметь принимать решения и понимать их
возможные последствия.
Слайд 3Теория принятия решений
Гипотеза
Используя теорию принятия решений на практике, можно успешно достигать
свои жизненные цели.
Слайд 4Теория принятия решений
Цель:
Доказать важность умения принимать оптимальное решение в сложных ситуациях,
используя теорию принятия решения на практике.
Слайд 5Теория принятия решений
Задачи:
Выяснить какие математические методы и способы можно использовать при
принятии оптимального решения в различных ситуациях .
Слайд 9Транспортные задачи
Предприятия
Потребители
Транспортные
затраты
Минимизировать затраты на перевозку грузов
Слайд 14Методы принятия решений
1. Решение задачи с помощью метода поэтапного сравнения.
2. Решение
задачи с помощью построения дерева решений.
3. Решение задачи с помощью бинарных решающих матриц.
4. Решение задачи с помощью таблицы оценок.
3. Решение задачи с помощью бинарных решающих матриц.
4. Решение задачи с помощью таблицы оценок.
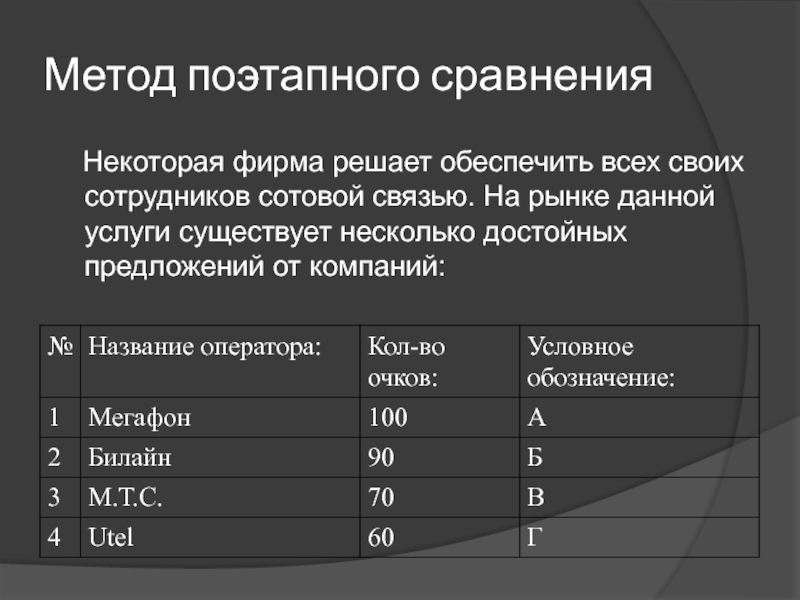
Слайд 15Метод поэтапного сравнения
Некоторая фирма решает обеспечить всех своих сотрудников
сотовой связью. На рынке данной услуги существует несколько достойных предложений от компаний:
Слайд 1628 вопросов-сравнений
1. Будет ли предложение А более важным, чем все
остальные 3 предложения, вместе взятые?
2. Будет ли предложение А более важным, чем предложения Б и В, вместе взятые?
3. Будет ли предложение А более важным, чем предложения Б и Г, вместе взятые?
4. Будет ли предложение А более важным, чем предложения В и Г, вместе взятые?
5. Будет ли предложение А более важным, чем предложение Б?
6. Будет ли предложение А более важным, чем предложение В?
7. Будет ли предложение А более важным, чем предложение Г?
8. Будет ли предложение Б более важным, чем предложения А, В, Г, вместе взятые?
9. Будет ли предложение Б более важным, чем предложения А, В, вместе взятые?
10. Будет ли предложение Б более важным, чем предложения А, Г, вместе взятые?
2. Будет ли предложение А более важным, чем предложения Б и В, вместе взятые?
3. Будет ли предложение А более важным, чем предложения Б и Г, вместе взятые?
4. Будет ли предложение А более важным, чем предложения В и Г, вместе взятые?
5. Будет ли предложение А более важным, чем предложение Б?
6. Будет ли предложение А более важным, чем предложение В?
7. Будет ли предложение А более важным, чем предложение Г?
8. Будет ли предложение Б более важным, чем предложения А, В, Г, вместе взятые?
9. Будет ли предложение Б более важным, чем предложения А, В, вместе взятые?
10. Будет ли предложение Б более важным, чем предложения А, Г, вместе взятые?
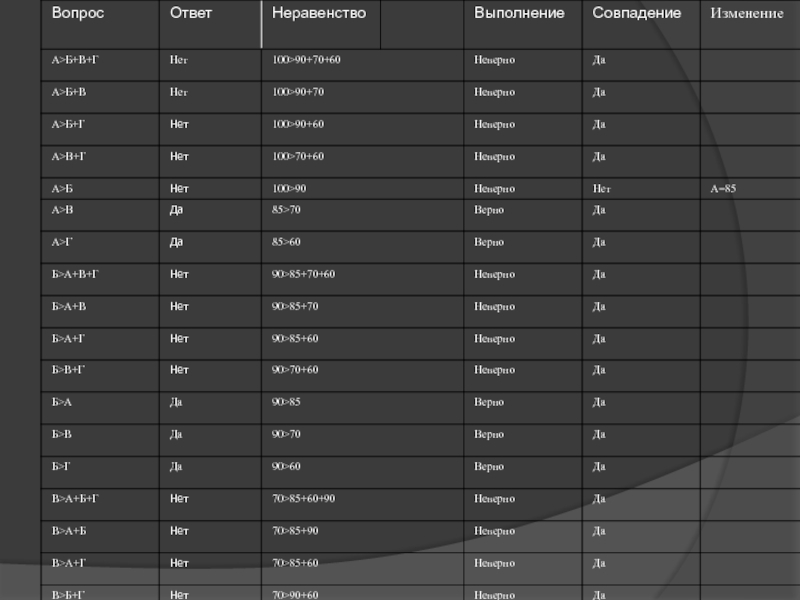
Слайд 17
Ответы на вопросы оформим в виде таблицы, где математический знак >
здесь означает «важнее чем».
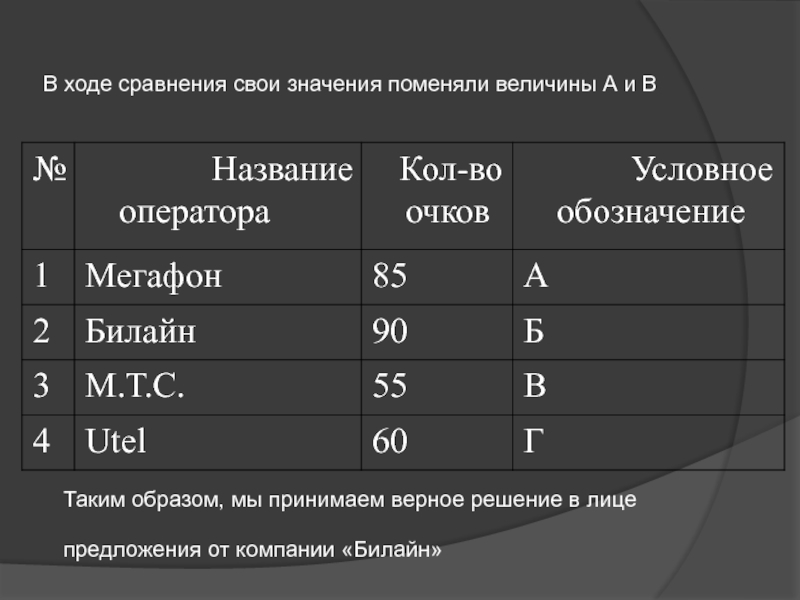
Слайд 19В ходе сравнения свои значения поменяли величины А и В
Таким
образом, мы принимаем верное решение в лице предложения от компании «Билайн»
Слайд 20Решение задачи с помощью построения дерева решений.
«С помощью дерева
решений сложное решение расчленяется на элементы, причём эти решения становятся всё более конкретными по мере того, как ветвление продвигается вниз»
Э. Науман
Э. Науман
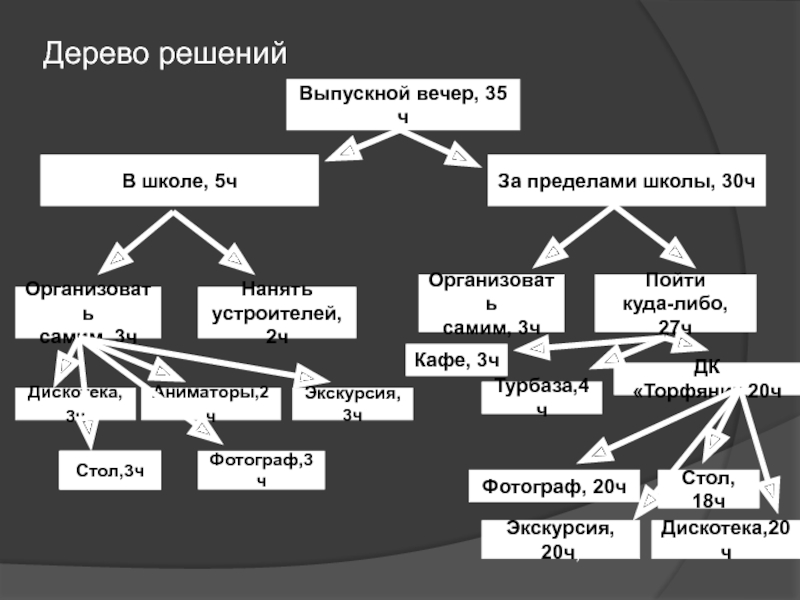
Слайд 23Дерево решений
Выпускной вечер, 35 ч
В школе, 5ч
За пределами школы, 30ч
Организовать
самим,
3ч
Нанять
устроителей, 2ч
Организовать
самим, 3ч
Пойти
куда-либо, 27ч
Дискотека,3ч
Стол
Аниматоры,2ч
Фотограф,3ч
Экскурсия,3ч
Кафе, 3ч
Турбаза,4ч
ДК «Торфяник,20ч
Дискотека,20ч
Стол
Стол,3ч
Стол, 18ч
Экскурсия, 20ч,
Фотограф, 20ч
Слайд 24Анализ результатов
По данным результатам можно непосредственно увидеть упорядоченную последовательность
вариантов решений. Наибольшая величина - встреча выпускного вечера в ДК «Торфяник», 57%
Слайд 25Бинарные решающие матрицы
Бинарные решающие матрицы представляют собой один из видов оценочных
таблиц. Столбцами таблицы, как правило, служат предложения, а строками – критерии оценки.
Слайд 26
1.Canon Ixus 750 (A)
2.Nikon Coolpix S1 (B)
3.Olympus FE-115 ZOOM (C)
4.Samsung
Digimax L-55 (D)
5.Genius G-Shot P 713 (E)
6.Sony DSC – T 9 (F)
7.Minolta Dimage Z-3 (G)
8.Kodak Easyshare V 550 (H)
9.Rekam Presto – T 65 (J)
5.Genius G-Shot P 713 (E)
6.Sony DSC – T 9 (F)
7.Minolta Dimage Z-3 (G)
8.Kodak Easyshare V 550 (H)
9.Rekam Presto – T 65 (J)
Слайд 27Критерии оценивания
1.Габариты, вес
2.Зум
3.Дисплей
4.Память
5.Питание
6.Наличие русифицированного меню
7.Разрешение снимков
8.Условия гарантии
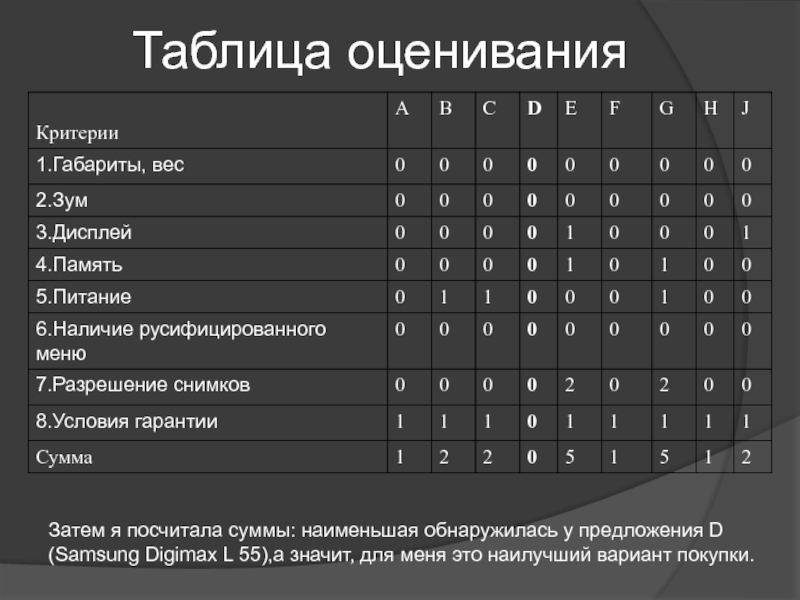
Слайд 28Таблица оценивания
Затем я посчитала суммы: наименьшая обнаружилась у предложения D (Samsung
Digimax L 55),а значит, для меня это наилучший вариант покупки.
Слайд 29Таблицы оценок
В таблице оценок различные варианты решений, критерии для выбора того
и иного варианта и оценочные характеристики сопоставляются таким образом, чтобы стало наглядной предпочтительность того и иного варианта.
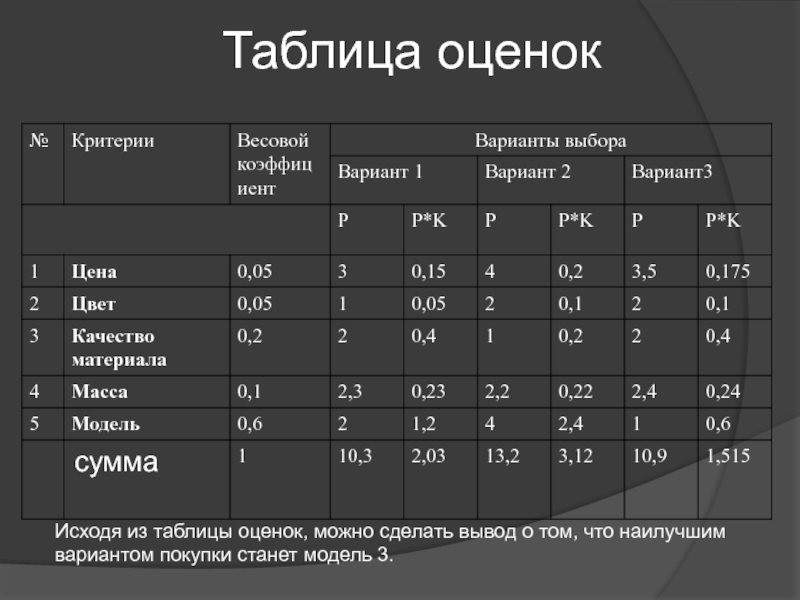
Слайд 33Таблица оценок
Исходя из таблицы оценок, можно сделать вывод о том, что
наилучшим
вариантом покупки станет модель 3.
вариантом покупки станет модель 3.
Слайд 34Вывод
На примере рассмотренных задач становится ясно насколько глубоко решения проникли в
нашу жизнь. Но каждый метод принятия решений, к сожалению, не даст вам гарантии 100% правильности. Это связано с тем, что, в любом случае, полностью объективную оценку ситуации получить практически нереально. Ведь каждый метод принятия решений зависит и от мнения коллектива людей, и от числовых значений.