- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи на смеси, сплавы, растворы
Содержание
- 1. Задачи на смеси, сплавы, растворы
- 2. Теоретические основы решения задач
- 3. Рассмотрим самый распространённый тип задач, где из
- 4. Исследуем это уравнение. Если взять два сплава,
- 5. А теперь приступим к выполнению задач.
- 6. Задача №1. Сплав олова с медью
- 7. Задача №2. Имеются две смеси
- 8. Задача №3. Сколько граммов 30%-ого
- 9. Задача №4. Даны два куска с
- 10. Задача №5. В 500 кг руды содержится
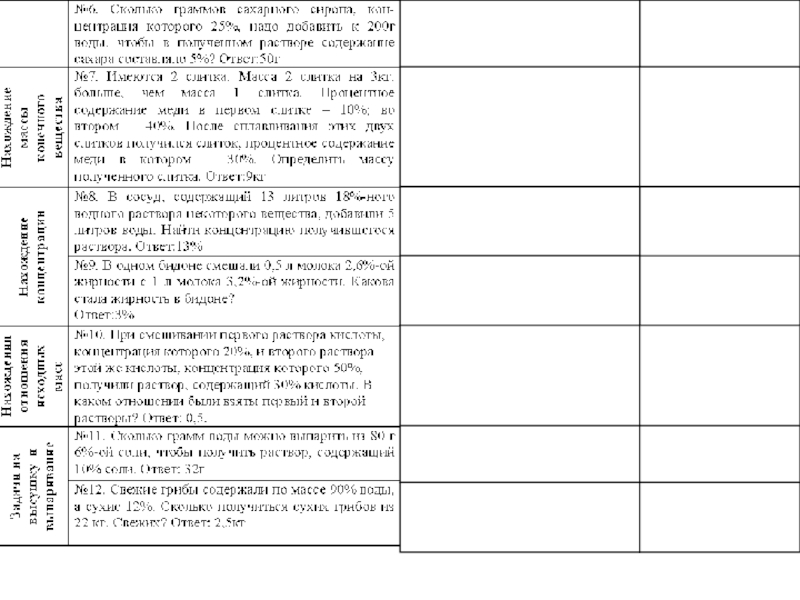
- 11. Задача №6. Арбуз весил 20 кг. и
- 12. Задача №7.В свежих яблоках 80% воды, а
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
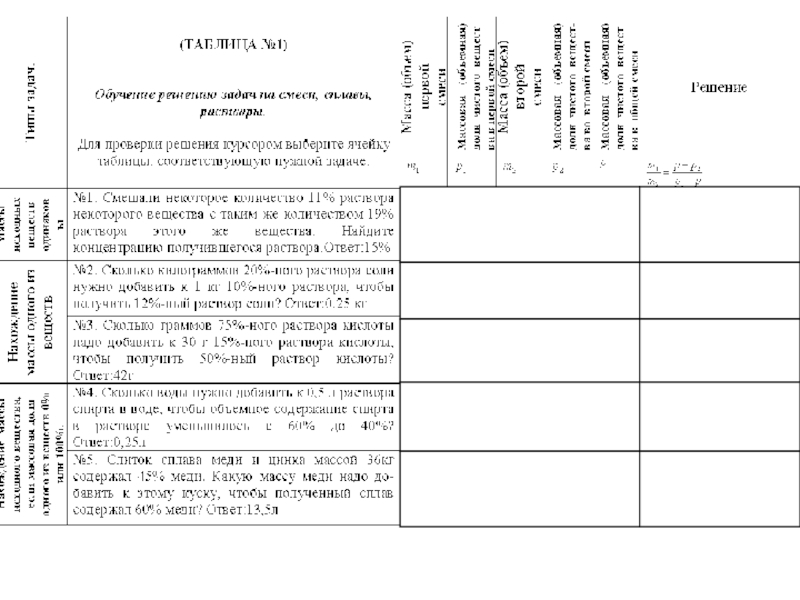
Теоретические основы решения задач «на смеси, сплавы, растворы» Перед
Слайд 2Теоретические основы решения задач
«на смеси, сплавы, растворы»
Перед тем, как приступить к решению подобных задач, примем некоторые допущения.
Все получающиеся сплавы или смеси однородны. При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси.
Это отношение может быть выражено либо в дробях, либо в процентах. Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества.
Все это синонимы.
В данной работе чаще упоминается термин «массовая доля», .
Концентрация – это безразмерная величина. Сумма массовых долей всех компонент, составляющих смесь, очевидно, равна единице.
Перед тем, как приступить к решению подобных задач, примем некоторые допущения.
Все получающиеся сплавы или смеси однородны. При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси.
Это отношение может быть выражено либо в дробях, либо в процентах. Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества.
Все это синонимы.
В данной работе чаще упоминается термин «массовая доля», .
Концентрация – это безразмерная величина. Сумма массовых долей всех компонент, составляющих смесь, очевидно, равна единице.
Слайд 3 Рассмотрим самый распространённый тип задач, где из двух смесей (сплавов, растворов)
получают новую смесь (сплав, раствор). Решим типовую задачу в общем виде, выведем формулу, а затем решим задачи с применением формулы.
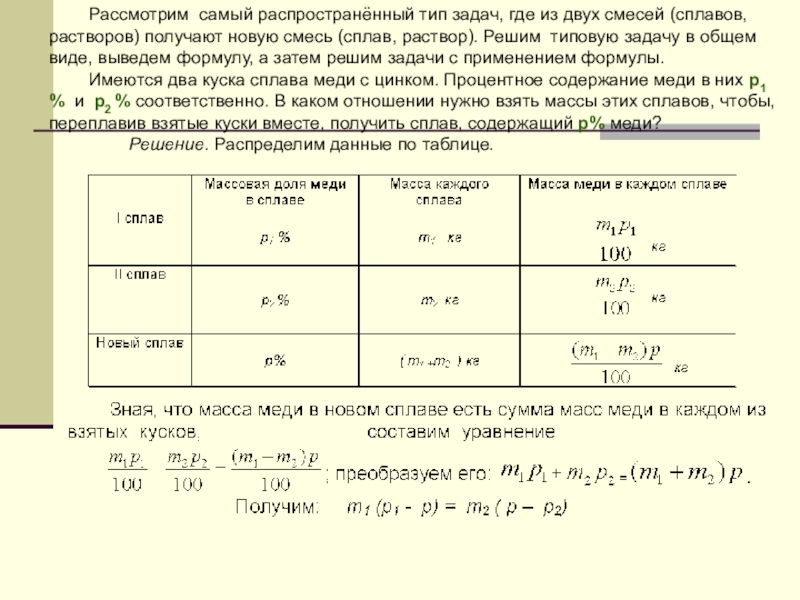
Имеются два куска сплава меди с цинком. Процентное содержание меди в них p1 % и p2 % соответственно. В каком отношении нужно взять массы этих сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий p% меди?
Решение. Распределим данные по таблице.
Имеются два куска сплава меди с цинком. Процентное содержание меди в них p1 % и p2 % соответственно. В каком отношении нужно взять массы этих сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий p% меди?
Решение. Распределим данные по таблице.
Слайд 4Исследуем это уравнение.
Если взять два сплава, массы которых одинаковы, т.е.
m1 = m2, то
Если исходные материалы имеют одинаковую процентную концентрацию, то концентрация конечного раствора не измениться.
Если р1, р2, р попарно не равны, то получим формулу:
Все рассуждения верны если вместо массовой доли дается объемная доля вещества в смеси.
Если исходные материалы имеют одинаковую процентную концентрацию, то концентрация конечного раствора не измениться.
Если р1, р2, р попарно не равны, то получим формулу:
Все рассуждения верны если вместо массовой доли дается объемная доля вещества в смеси.
Слайд 6Задача №1. Сплав олова с медью весом 12кг содержит 45% меди.
Сколько чистого олова нужно добавить, чтобы получить сплав, содержащий 40% меди.
12кг
45%
40%
0%
Слайд 7Задача №2. Имеются две смеси апельсинового сока. Первая смесь 40%-ого
сока, а вторая – 80%. Смешивают несколько литров первой смеси и второй, в результате получается 20 л смеси, содержащей 70% апельсинового сока. Найти, сколько литров 40%-ого сока брали.
40%
70%
80%
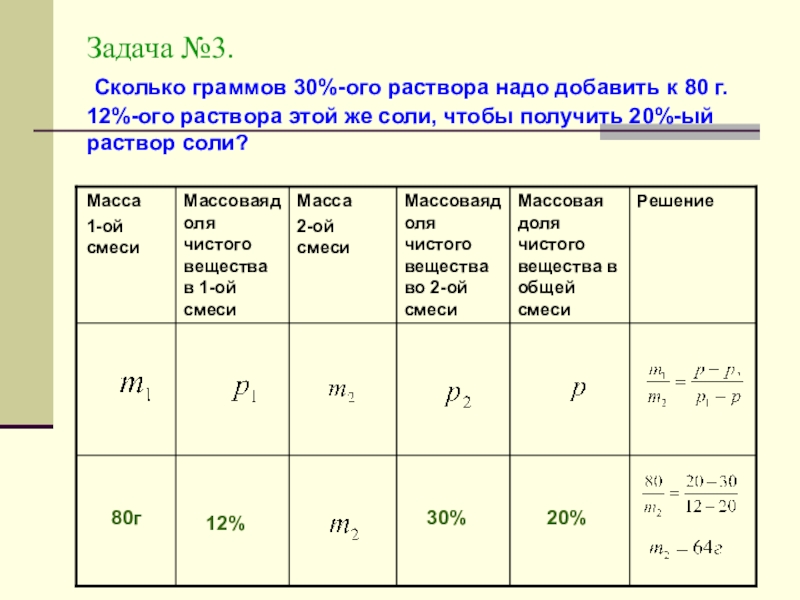
Слайд 8Задача №3. Сколько граммов 30%-ого раствора надо добавить к 80
г.
12%-ого раствора этой же соли, чтобы получить 20%-ый
раствор соли?
12%
20%
30%
80г
Слайд 9Задача №4. Даны два куска с разным содержанием олова. Первый, массой
300г, содержит 20% олова, а 2-ой, массой 200г-40%. Сколько % олова будет содержать сплав, полученный из данных кусков.
20%
40%
300г
200гр.
Слайд 10Задача №5. В 500 кг руды содержится некоторое количество железа. После
удаления из руды 200 кг примесей, содержащих в среднем 12,5% железа, содержание железа в оставшейся руде повысилось на20%. Определите, сколько процентов железа осталось ещё в руде.
300кг
200кг
12,5%
Слайд 11Задача №6. Арбуз весил 20 кг. и содержал 99% воды, когда
он немного усох, то стал содержать 98% воды. Сколько теперь весит арбуз?
98%
99%
100%
Слайд 12Задача №7.В свежих яблоках 80% воды, а в сушеных – 20%.
На сколько процентов уменьшается масса яблок при сушке?
20%
80%
100%