- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Вневписанная окружность треугольника
Содержание
- 1. Вневписанная окружность треугольника
- 2. Вневписанной окружностью треугольника называется окружность, к которой
- 3. Соотношение между длинами отрезков касательныхТеорема 1: Расстояние
- 4. Следствие 1: Прямая, проведенная через вершину треугольника
- 5. Следствие 2: Для отрезков касательных, связанных с
- 6. Формулы для вычисления радиусов вневписанных окружностейТеорема 2:
- 7. Следствие 1: Большей стороне треугольника соответствует касающаяся
- 8. Следствие 4: Для отношения радиусов вписанной и
- 9. Теорема 3: Радиус вневписанной окружности, касающейся боковой
- 10. Следствие: В равнобедренном треугольнике расстояние от вершины,
- 11. Теорема 4: Радиусы вневписанных окружностей выражаются через
- 12. Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы
- 13. Следствие: Т.к. для прямоугольного треугольника имеют место
- 14. Теорема 6: Гипотенуза прямоугольного треугольника равна сумме
- 15. Следствие: Т.к. rc = c + r,
- 16. Теорема 7: Доказать, что катеты прямоугольного треугольника
- 17. Расстояния до центров вневписанных окружностей
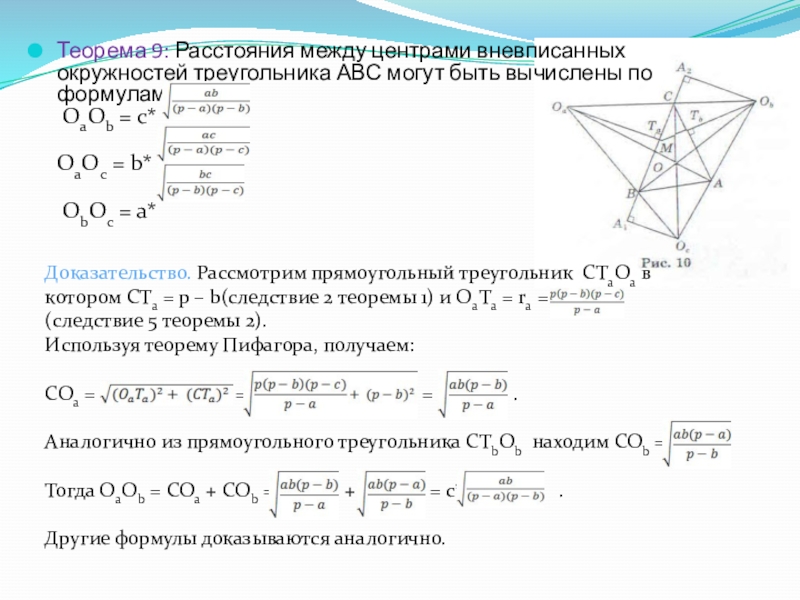
- 18. Теорема 9: Расстояния между центрами вневписанных окружностей
- 19. Следствие. Расстояния от вершины С треугольника АВС
- 20. Соотношения между величинами угловТеорема 10: Сторона ВС
Слайд 2Вневписанной окружностью треугольника называется окружность, к которой являются касательными одна из
Слайд 3Соотношение между длинами отрезков касательных
Теорема 1: Расстояние от вершины треугольника до
Доказательство. Обозначим через В₁, С₁, и Та – точки касания вневписанной окружности с прямыми АС, АВ и ВС соответственно. Тогда СВ₁ = СТа, ВС₁ = ВТа и периметр треугольника АВС: P = AC + СТа + ВТа + АВ = АС + СВ₁ + ВС₁ + АВ = АВ₁ + АС₁. Т.к. АВ₁ = АС₁, то расстояния АВ₁ и АС₁ равны полупериметру треугольника АВС.
Слайд 4Следствие 1: Прямая, проведенная через вершину треугольника и точку, в которой
Примечание: В треугольнике расстояние от вершины треугольника до точки касания вписанной окружности со стороной треугольника, выходящей из данной вершины, есть разность полупериметра треугольника и стороны, противолежащей данной вершине. То же соблюдается и для вневписанной окружности. AN = AK = p – a, BM = BK = p – b, CN = CM = p – c.
Слайд 5Следствие 2: Для отрезков касательных, связанных с вневписанными окружностями треугольника, выполняются
Следствие 3: Верны следующие равенства: B2Tb = C2Tc = ATc + ATb = a, C1Tc = A1Ta = BTc + BTa = b, B1Tb = A2Ta = CTb + CTa = c.
Следствие 4: Расстояния между точками касаний вневписанных окружностей продолжений сторон за вершины треугольника равны: C1C2 = a +b, B1B2 = a + c, A1A2 = b + c.
Из следствия 1
Получаются при попарном сложении равенств из следствия 2
Получаются при попарном сложении равенств из следствия 3
Слайд 6Формулы для вычисления радиусов вневписанных окружностей
Теорема 2: Радиус вневписанной окружности, касающейся
Доказательство. Выполняются следующие равенства:
SABC = SOCA + SOBA - SOCB = 0,5rab + 0,5rac – 0,5raa = ra(p -a).
Аналогично получаются формулы:
rb = и rc =
Слайд 7Следствие 1: Большей стороне треугольника соответствует касающаяся её вневписанная окружность большего
Следствие 2: Радиус вневписанной окружности треугольника больше радиуса окружности, вписанной в тот же треугольник.
Следствие 3: Площадь треугольника АВС может быть вычислена по формулам: S = ra(p - a), S = rb(p - b), S = rc(p - c).
Слайд 8Следствие 4: Для отношения радиусов вписанной и вневписанных окружностей имеют место
Следствие 5: Используя формулу Герона, получим формулы для вычисления длин радиусов через стороны треугольника: ra = rb = rc =
Слайд 9Теорема 3: Радиус вневписанной окружности, касающейся боковой стороны равнобедренного треугольника, равен
Доказательство. Пусть Oa, Ob и Oc – центры вневписанных окружностей треугольника АВС, Ca, Cb и Tc – точки касания этих окружностей с прямой АВ.
Т.к. треугольник АВС – равнобедренный (АС = ВС), то высота, опущенная из вершины С, лежит на биссектрисе СОс угла С, и поэтому СОс ⊥ АВ. С другой стороны радиус ОсТс ⊥ АВ, следовательно, точка Тс лежит на биссектрисе угла С. Отсюда ОТс ⊥ АВ и СТс является высотой треугольника АВС. Заметим, что СОс ⊥ COb как биссектрисы внутреннего и внешнего угла треугольника при вершине С, СОс ⊥ АВ и ObCb ⊥ АВ. Следовательно, четырехугольник TcCObCb – прямоугольник. Значит, rb = ObCb = CTc.
Слайд 10Следствие: В равнобедренном треугольнике расстояние от вершины, лежащей напротив основания, до
Слайд 11Теорема 4: Радиусы вневписанных окружностей выражаются через стороны равнобедренного треугольника формулами:
Доказательство. Из доказательства теоремы 3 следует, что CTc ⊥ AB и BTc = ATc = 0,5c. Из прямоугольного треугольника
TcCA rb = CTc =
Прямоугольные треугольники ОсТсА и ObCbA подобны по двум углам. Тогда
= = = . Отсюда = или rc =0,5c *
Следствие. Для равностороннего треугольника ra = rb = rc = =3r, где а – сторона треугольника и r – радиус вписанной окружности.
Слайд 12Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы прямоугольного треугольника, равен полупериметру
Доказательство. Пусть вневписанная окружность с центром в Ос касается продолжений катетов СВ и СА в точках А3 и В3 соответственно.
Радиусы, проведенные в точки касания, перпендикулярны прямым СВ и СА. Из теоремы 1 отрезки СА3 = СВ3 = p. Т.к. четырехугольник СВ3ОсА3 – квадрат, то rc = ОсА3 = СА3 = p.
Слайд 13Следствие: Т.к. для прямоугольного треугольника имеют место формулы p = 2R
Слайд 14Теорема 6: Гипотенуза прямоугольного треугольника равна сумме радиусов вневписанных окружностей, касающихся
Доказательство. Т.к. четырехугольники СТаОаВ1 и СА1ОbTb – квадраты, то CTa = ra, CTb = rb. Из следствия 3 теоремы 1 имеем ra + rb = CTa + CTb = c.
Слайд 16Теорема 7: Доказать, что катеты прямоугольного треугольника АВС с прямым углом
Доказательство. а) По следствию 2 теоремы 1 имеем rb = CTb = p – a. Т.к. по теореме 5 rc = p, то получаем a = rc – rb. Вторая формула доказывается аналогично.
б) Т.к. центры вневписанных окружностей Oa и Ос лежат на биссектрисе внешнего угла В треугольника АВС, то прямоугольные треугольники ОаТаВ и ОсА3В подобны по двум углам. Тогда из равенства отношения сторон, лежащих против равных углов, ОаТа/ОсА3 = ТаВ/ВА3, получаем ra/rc = a – ra/rc – a. Отсюда a = 2rarc / ra + rc.
Следствие. Из первых двух формул теоремы 7 получаем |a – b| = |ra – rb|.
Слайд 18Теорема 9: Расстояния между центрами вневписанных окружностей треугольника АВС могут быть
OaOc = b*
ObOc = a*
Доказательство. Рассмотрим прямоугольный треугольник CTaOa в котором CTa = p – b(следствие 2 теоремы 1) и OaTa = ra = (следствие 5 теоремы 2).
Используя теорему Пифагора, получаем:
СОа = = = .
Аналогично из прямоугольного треугольника CTbOb находим COb =
Тогда OaOb = COa + COb = + = c* .
Другие формулы доказываются аналогично.
Слайд 19Следствие. Расстояния от вершины С треугольника АВС до центров Oa и
Замечание. Из прямоугольного треугольника СОсА1 можно найти расстояние от вершины С треугольника АВС до центра Ос вневписанной окружности: СОс = =
Слайд 20Соотношения между величинами углов
Теорема 10: Сторона ВС треугольника АВС видна из
Доказательство. Т.к. BOa и COa – биссектрисы внешних углов треугольника АВС при вершинах В и С, то СВОа = 90 - и ВСОа = 90 - .
Отсюда получаем ВОаС = 180 - СВОа - ВСОа = 180 - (90 - + 90 - ) = 90 -