©
Москва, 2016 г
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Влияние индивидуальных особенностей математического мышления на процесс решения задач
Содержание
- 1. Влияние индивидуальных особенностей математического мышления на процесс решения задач
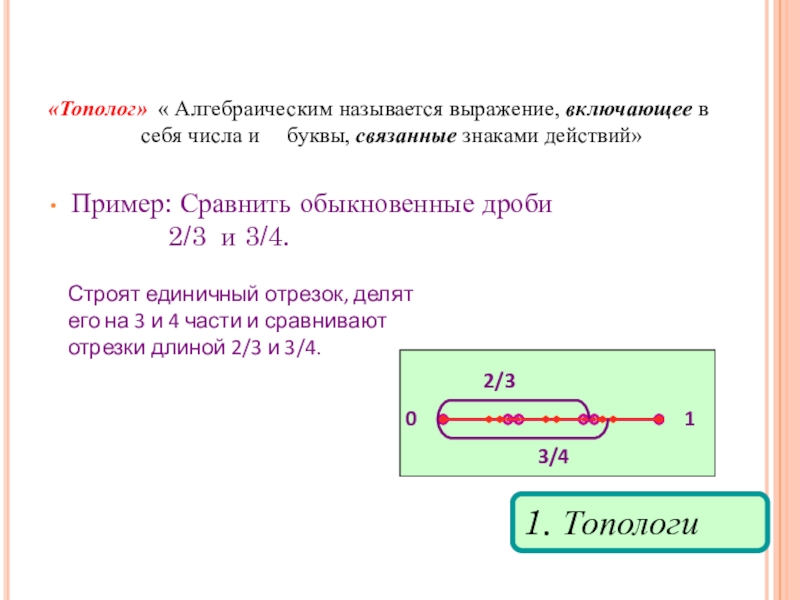
- 2. «Тополог» « Алгебраическим называется выражение, включающее в
- 3. 2. Проективисты«Проективист» «Алгебраическим называется выражение подобное, например,
- 4. «Порядковец» «Алгебраическим можно назвать выражение , в
- 5. «Метрист» «Алгебраическое выражение представляет собою определенное количество
- 6. 2. АлгебраистыДополняют каждую дробь до целого(до 1):Пример:
- 7. Урок по теме «Соотношение между сторонами и углами треугольника»
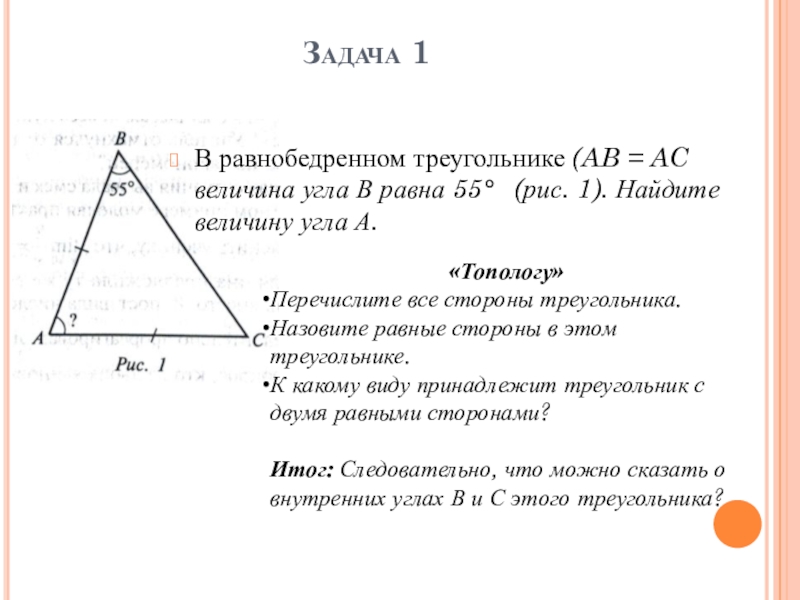
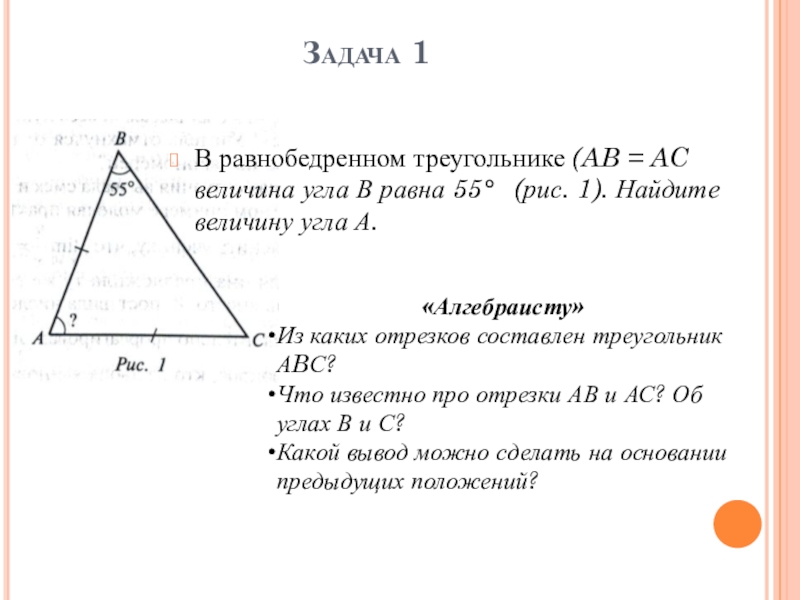
- 8. Задача 1В равнобедренном треугольнике (AB = AC
- 9. Задача 1В равнобедренном треугольнике (AB = AC
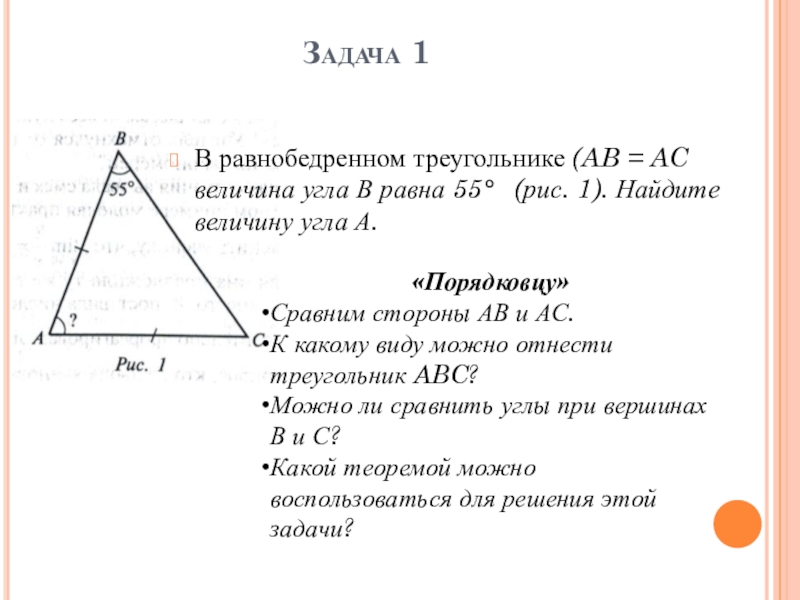
- 10. Задача 1В равнобедренном треугольнике (AB = AC
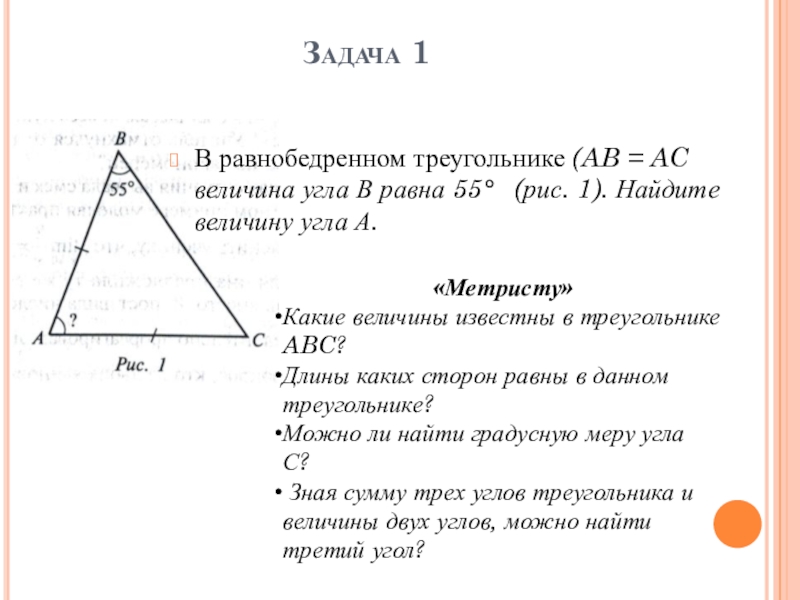
- 11. Задача 1В равнобедренном треугольнике (AB = AC
- 12. Задача 1В равнобедренном треугольнике (AB = AC
- 13. Задача 2 Сравнить по рис. 2 величины
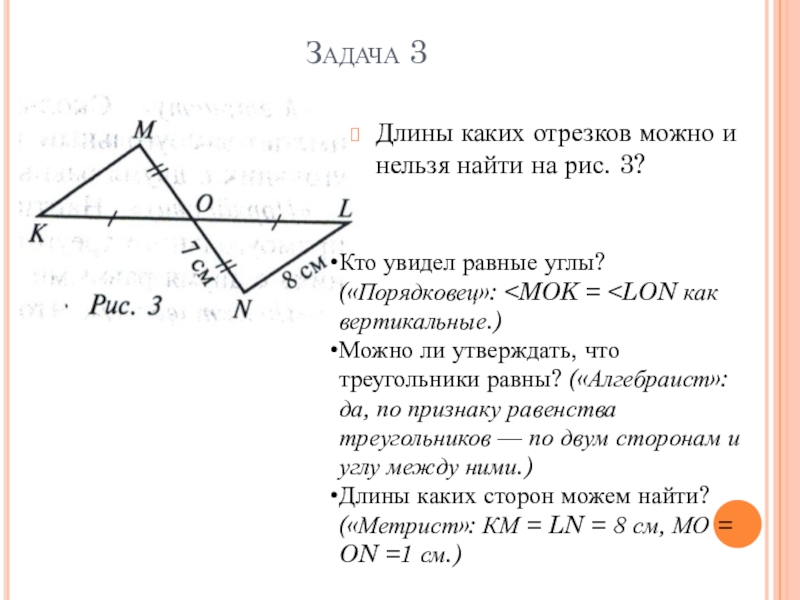
- 14. Задача 3Длины каких отрезков можно и нельзя найти на рис. 3?Кто увидел равные углы? («Порядковец»:
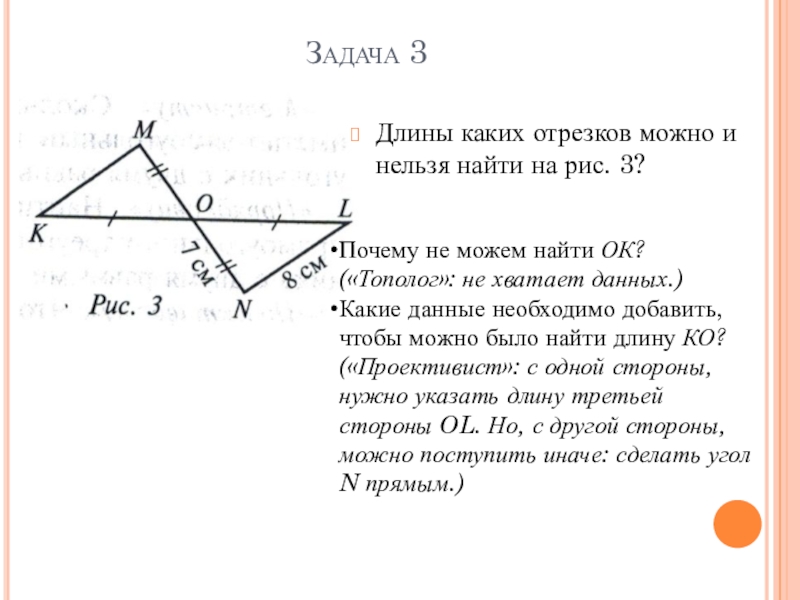
- 15. Задача 3Длины каких отрезков можно и нельзя
- 16. Спасибо за внимание!
«Тополог» « Алгебраическим называется выражение, включающее в себя числа и буквы, связанные знаками действий»Пример: Сравнить обыкновенные дроби 2/3 и 3/4. 1. ТопологиСтроят единичный отрезок, делят его на 3 и 4 части и сравнивают отрезки
Слайд 1Влияние индивидуальных особенностей математического мышления на процесс решения задач
Жданов Александр Александрович
Слайд 2
«Тополог» « Алгебраическим называется выражение, включающее в себя числа и
буквы, связанные знаками действий»
Пример: Сравнить обыкновенные дроби 2/3 и 3/4.
Пример: Сравнить обыкновенные дроби 2/3 и 3/4.
1. Топологи
Строят единичный отрезок, делят его на 3 и 4 части и сравнивают отрезки длиной 2/3 и 3/4.
Слайд 32. Проективисты
«Проективист» «Алгебраическим называется выражение подобное, например, предложению в русском языке:
как в языке задаются соответствующие слова, знаки препинания, так и в алгебраическом выражении заданы числа, буквы и знаки действий между ними»
Пример: Сравнить обыкновенные дроби
2/3 и 3/4.
Слайд 4«Порядковец» «Алгебраическим можно назвать выражение , в котором числа и буквы
взаимодействуют друг с другом по конкретным правилам, строго определяемым законами, зафиксированными знаками математических действий»
Пример: Сравнить обыкновенные дроби 2/3 и 3/4.
Пример: Сравнить обыкновенные дроби 2/3 и 3/4.
3. Порядковисты
Уравнивают знаменатели и сравнивают числители:
Слайд 5
«Метрист» «Алгебраическое выражение представляет собою определенное количество букв, чисел и знаков
действий (то, что можно записать с помощью одной или нескольких букв, чисел и знаков действий). При этом заменяя буквы числами, всегда можно найти его конкретное числовое значение»
4. Метристы
Работают с числами, составляют пропорции:
Пример: Сравнить обыкновенные дроби
2/3 и 3/4.
Слайд 62. Алгебраисты
Дополняют каждую дробь до целого(до 1):
Пример: Сравнить обыкновенные дроби
2/3 и
3/4.
«Алгебраист» «Алгебраическое выражение состоит из чисел, букв и знаков действий»
Слайд 8Задача 1
В равнобедренном треугольнике (AB = AC величина угла В равна
55° (рис. 1). Найдите величину угла А.
«Топологу»
Перечислите все стороны треугольника.
Назовите равные стороны в этом треугольнике.
К какому виду принадлежит треугольник с двумя равными сторонами?
Итог: Следовательно, что можно сказать о внутренних углах В и С этого треугольника?
Слайд 9Задача 1
В равнобедренном треугольнике (AB = AC величина угла В равна
55° (рис. 1). Найдите величину угла А.
«Проективисту»
Можно ли, глядя на рис. 1, определить вид треугольника по его сторонам?
Какие свойства равнобедренного треугольника могли бы помочь решить задачу?
Какую сторону в этом треугольнике можно было бы считать основанием?
Если треугольник ABC равнобедренный, то что известно про его углы при основании?
Слайд 10Задача 1
В равнобедренном треугольнике (AB = AC величина угла В равна
55° (рис. 1). Найдите величину угла А.
«Порядковцу»
Сравним стороны АВ и АС.
К какому виду можно отнести треугольник ABC?
Можно ли сравнить углы при вершинах В и С?
Какой теоремой можно воспользоваться для решения этой задачи?
Слайд 11Задача 1
В равнобедренном треугольнике (AB = AC величина угла В равна
55° (рис. 1). Найдите величину угла А.
«Метристу»
Какие величины известны в треугольнике ABC?
Длины каких сторон равны в данном треугольнике?
Можно ли найти градусную меру угла С?
Зная сумму трех углов треугольника и величины двух углов, можно найти третий угол?
Слайд 12Задача 1
В равнобедренном треугольнике (AB = AC величина угла В равна
55° (рис. 1). Найдите величину угла А.
«Алгебраисту»
Из каких отрезков составлен треугольник АBС?
Что известно про отрезки АВ и АС? Об углах В и С?
Какой вывод можно сделать на основании предыдущих положений?
Слайд 13Задача 2
Сравнить по рис. 2 величины углов 1 и 2.
«Тополог».
Всевозможные внутренние и внешние углы треугольника.
«Проективист». Лучи, выходящие из вершин треугольника.
«Порядковец». Смежные и вертикальные углы.
«Метрист». Три пересекающиеся прямые и два угла при них.
«Алгебраист». Треугольник, множество углов, среди которых выделены его внешний и внутренний углы.
«Проективист». Лучи, выходящие из вершин треугольника.
«Порядковец». Смежные и вертикальные углы.
«Метрист». Три пересекающиеся прямые и два угла при них.
«Алгебраист». Треугольник, множество углов, среди которых выделены его внешний и внутренний углы.
Слайд 14Задача 3
Длины каких отрезков можно и нельзя найти на рис. 3?
Кто
увидел равные углы? («Порядковец»: Можно ли утверждать, что треугольники равны? («Алгебраист»: да, по признаку равенства треугольников — по двум сторонам и углу между ними.)
Длины каких сторон можем найти? («Метрист»: КМ = LN = 8 см, МО = ON =1 см.)
Длины каких сторон можем найти? («Метрист»: КМ = LN = 8 см, МО = ON =1 см.)
Слайд 15Задача 3
Длины каких отрезков можно и нельзя найти на рис. 3?
Почему
не можем найти ОК? («Тополог»: не хватает данных.)
Какие данные необходимо добавить, чтобы можно было найти длину КО? («Проективист»: с одной стороны, нужно указать длину третьей стороны OL. Но, с другой стороны, можно поступить иначе: сделать угол N прямым.)
Какие данные необходимо добавить, чтобы можно было найти длину КО? («Проективист»: с одной стороны, нужно указать длину третьей стороны OL. Но, с другой стороны, можно поступить иначе: сделать угол N прямым.)
