- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Узагальнення та систем атизація знань учнів на уроках математики
Содержание
- 1. Узагальнення та систем атизація знань учнів на уроках математики
- 2. Слайд 2
- 3. Первинне узагальненняПриватне або понятійне узагальненняПоурочне узагальнення та
- 4. Первинне узагальнення Урок алгебри 9 клас Тема
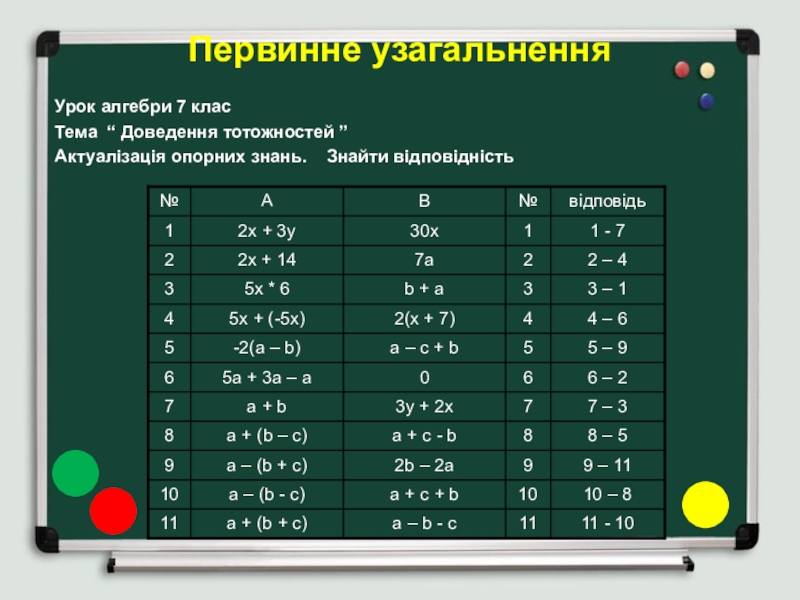
- 5. Первинне узагальненняУрок алгебри 7 клас Тема “ Доведення тотожностей ”Актуалізація опорних знань. Знайти відповідність
- 6. Первинне узагальненняУрок геометрії 7 клас Тема “
- 7. Приватне або понятійне узагальненняУрок математики 6 класТема
- 8. Приватне або понятійне узагальненняУрок геометрії 8 класТема
- 9. Слайд 9
- 10. Тематичне узагальнення та систематизація
- 11. Підсумкове узагальненняМета тематичного повторення та підсумкового аналогічні.
- 12. Міжпредметне узагальненняАлгебраїчним способом розв'язується багато задач з
Слайд 1Майстер-клас
Узагальнення та систематизація знань на уроках математики
Пащенко Вікторія Вікторівна
Вчитель Гірницької ЗОШ
Селидівської міської ради
Слайд 2
«Голова, наполненная отрывочными,
Ушинский К.Д.
Слайд 3Первинне узагальнення
Приватне або понятійне узагальнення
Поурочне узагальнення та систематизація
Тематичне узагальнення та систематизація
Підсумкове
Міжпредметне узагальнення та систематизація
Етапи узагальнення та систематизації знань
Слайд 4Первинне узагальнення
Урок алгебри 9 клас
Тема “ Графік квадратичної функції ”
Актуалізація
х2 - 9 х + 20 назвати коефіцієнти та знайти корені тричлена
х2 - 9 х + 20 = 0 розв'язати рівняння
х2 - 9 х + 20 розкласти тричлен на множники
у = х2 -9 х + 20 описати графік функції
х2 - 9 х + 20 < 0 розв'язати нерівність
х2 - 9 х + 20 скоротити дріб
(х - 5)
у = х2 - 9 х + 20 описати графік функції
(х - 5)
Слайд 5Первинне узагальнення
Урок алгебри 7 клас
Тема “ Доведення тотожностей ”
Актуалізація опорних
Слайд 6Первинне узагальнення
Урок геометрії 7 клас
Тема “ Сума кутів трикутника ”
Актуалізація
При ознайомленні з новим матеріалом, учням пропонується самостійно
довести теорему про суму кутів трикутника за допомогою малюнків, розглянутих
на початку уроку. Склавши умови для первинного узагальнення та
систематизації знань, учні мають можливість легко та без будь яких зусиль
впоратися з поставленою задачею.
“
Слайд 7Приватне або понятійне узагальнення
Урок математики 6 клас
Тема “ Паралельні прямі “
На
прямих, які не мають спільних точок. При цьому пари
займають різне положення на площині Серед них є
горизонтальні, вертикальні, похилі, у двох різних
парах відстань між непересічними прямими також
різна. Корисно також показати пари прямих, які в
полі дошки не перетинаються, але є вірогідність того,
що вони перетнуться при продовженні. Учні
виділяють пари прямих, які мають певно загальні
ознаки: один клас – прямі , які перетинаються, і
другий клас – прямі, які не перетинаються. Називаючи
загальну суттєву ознаку, учні відволікаються від
положення на площині відстані між прямими в двох різних
парах. Узагальнення відбувається тоді , коли вводиться
термін “ паралельні прямі ” і відповідний символ.
Слайд 8Приватне або понятійне узагальнення
Урок геометрії 8 клас
Тема
“ Квадрат та його
Учням пропонується самостійно дати
означення квадрату. Діти дають багато
правильних відповідей, завдяки яким вони
роблять висновок, що квадрат – це фігура,
яка водночас являється і паралелограмом, і
прямокутником. І ромбом. Всі відповіді
приймаються, але слід відмітити саме
коротше означення квадрата. Яке
вважається більш раціональним. Далі учням
пропонується самостійно визначити
властивості квадрата, де учні згадують
властивості усіх видів паралелограму,
повторюють і систематизують їх. Такий
прийом можна також віднести і до
поурочного узагальнення. Він дозволяє
виявити між поняттями, які вивчаються,
загальні ознаки та властивості, об'єднати засвоєнні
поняття в систему, розкрити зв'язки та відношення
між елементами даної системи.
Слайд 9 Поурочне узагальнення Урок геометрії
Завдання: які з наданих властивостей
однозначно визначають основне поняття
теми?
Діагоналі взаємно перпендикулярні.
Многокутник
Діагоналі точкою перетину діляться навпіл.
Протилежні сторони попарно рівні.
Має чотири і тільки чотири кута
Має хоч би один прямий кут
Діагоналі рівні між собою.
Чотирикутник.
Дві суміжні сторони рівні між собою.
Паралелограм.
Чотири сторони і чотири кута рівні між собою.
Прямокутник.
Ромб.
Відповіді:
Учні можуть обрати різні сукупності
значущих ознак, однозначно визначаючи
одне й теж поняття.
Чотирикутник = 2 + 5;
Паралелограм = 8 + 4;
Паралелограм = 8 + 3;
Паралелограм = 2 + 5 + 4;
Ромб = 10 + 9
Квадрат = 2 + 5 + 4 + 9 + 6;
Квадрат = 12 + 9;
Ромб = 8 + 3 + 1;
Ромб = 10 + 1;
Квадрат = 13 + 6;
Квадрат = 10 + 11;
Квадрат = 10 + 9 + 7;
Прямокутник = 10 + 6;
Прямокутник = 8 + 3 + 6
Слайд 10Тематичне узагальнення та систематизація
Прикладом тематичного узагальнення можна
Схеми виступають як моделі структури учбового матеріалу і як засіб кращого відображення цієї
структури в розумінні учня.
В своїй практиці я багато років веду з учнями зошити – конспекти, які діти заводять у 5 класі
і продовжують їх до випускного класу. У цих зошитах діти записують головне з кожної теми:
означення, формули, властивості, приклади розв'язання вправ. Записи дозволяю робити
різними кольорами, що на початку приваблює п'ятикласників. Мета полягає в тому, що учні з
самого початку навчаються виділяти саме головне у темі, робити опорні конспекти. По цим
конспектам вони готуються до контрольних робіт. В п'ятому класі я працюю разом з дітьми. У
шостому класі при вивчені нової теми складання конспектів не відбувається, тому що складання
опорного конспекту задаю як домашнє завдання. Вдома матеріал підручника опрацьовується і
головне на думку учня записується у зошит – конспект. Наявність опорного конспекту є
обов'язковим. Це примушує учнів вивчати теоретичний матеріал, а не тільки розв'язувати
приклади та задачі. Ця робота продовжується і в 7 класі. Але для учнів, які мають
достатній і високий рівень навчання ще пропонується заносити у зошит вивід
формул, доведення теорем. У наступних класах ця робота для учнів стає
звичайною.
Слайд 11Підсумкове узагальнення
Мета тематичного повторення та підсумкового аналогічні. Матеріали повторення
дуже близькі.
систематизація та узагальнення спрямовані на:
Повторення основних понять, вагомих ідей курсу;
Нагадування у можливо крупних рисах пройденого шляху, еволюції понять, їх розвитку, їх теоретичних та практичних додатків;
Поглиблення, та по можливості розширення знань учнів по основним питанням курсу;
Формування іншого підходу до раніше вивченого матеріалу, приєднання до повторного матеріалу нових знань.
На етапі підсумкового узагальнення корисно використовувати нестандартні задачі
такі як, розв'язати рівняння:
Слайд 12Міжпредметне узагальнення
Алгебраїчним способом розв'язується багато задач з геометрії,
фізики, хімії, астрономії. У
означення, типові для даної науки, а математичний матеріал, який
використовується для них, то й самий. Міжпредметне узагальнення
здійснюється на ряду суміжних предметів. У загальній схемі
розв'язування фізичних задач виділяють: аналіз фізичної суті, перевід
значень фізичних величин до одиниць системи СІ. Останні дії , по
суті, співпадають з діями, визначеними загальним прийомом
розв'язування задач за допомогою складання рівнянь в алгебрі. У всіх
випадках учням не потрібно вивчати спеціальні способи розв'язання
фізичних задач. Вони повинні розумно використовувати прийоми
розв'язування, сформульовані на уроках математики.