- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок на тему: Логарифмическая функция, её свойства и график(презентация)
Содержание
- 1. Урок на тему: Логарифмическая функция, её свойства и график(презентация)
- 2. Работа устно:Работа устно:НЕПЕР
- 3. Задача дня Изобразить схематически график функции
- 4. ёДжон НеперJohn NapierДата рождения: 1550 годМесто рождения: замок
- 5. Прочитайте и назовите график функции, изображённый на рисунке.0y11xПланКакими свойствами обладают показательные функции?
- 6. План исследования функции:1) D(f) – область определения
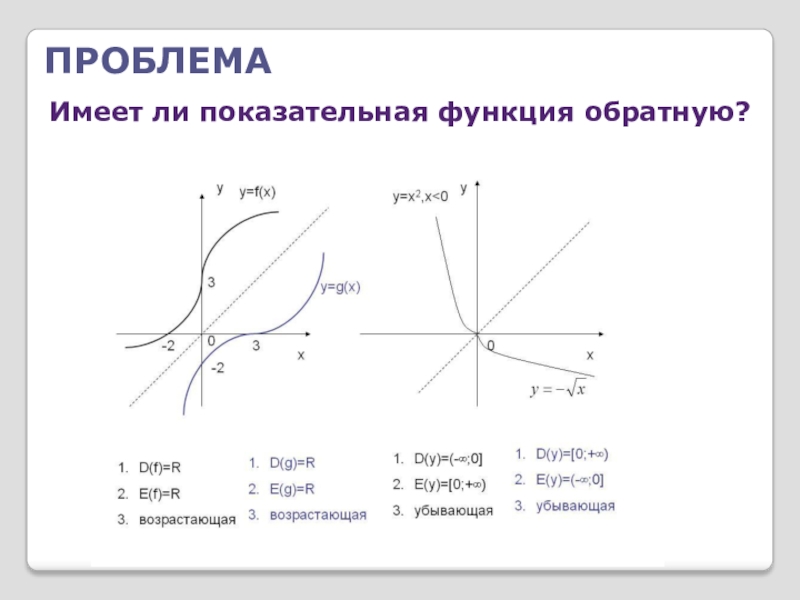
- 7. ПроблемаИмеет ли показательная функция обратную?
- 8. Примеры нахождения обратных функций:Найти функцию, обратную к
- 9. через уПрименим данный алгоритм для нахождения функции,
- 10. через у График функции
- 11. через у График функции
- 12. Вывод:Обратную функцию
- 13. xy01231248- 1- 2График функции y = loga
- 14. через у1) D(f) = (0, + ∞);2)
- 15. через у1) D(f) = (0, + ∞);2)
- 16. №318 Сравнить
- 17. №319 Выяснить, является ли положительным или отрицательным число:1)1544,5положительное число10,452)отрицательное число3)125,3положительное число19,64)отрицательное число
- 18. Обучающий тестКакие из следующих графиков не могут
- 19. Задача дняИзобразить схематически график функции: Решение:Область определения
- 20. y12x-13
- 21. § 18 №324, 3321 вариант – 1,3;2 вариант – 2,4.Удачи
- 22. Список литературы•Алгебра и начала анализа: Учеб. Для
Слайд 1Логарифмическая функция, её свойства
и график
МБОУ СОШ №22
города Асбеста
Свердловской области
Костюкова Галина Аркадьевна
Слайд 4ё
Джон Непер
John Napier
Дата рождения:
1550 год
Место рождения:
замок Мерчистон, в те годы
Дата смерти:
4 апреля 1617
Место смерти:
Эдинбург
Научная сфера:
математика
Альма-матер:
Сент-Эндрюсский университет
Известен как:
изобретатель логарифмов
Слайд 5Прочитайте и назовите график функции,
изображённый на рисунке.
0
y
1
1
x
План
Какими свойствами обладают
Слайд 6План исследования функции:
1) D(f) – область определения функции.
2) E(f) – область
3) Промежутки возрастания, убывания функции.
4) Чётность, нечётность функции .
5) Наибольшие, наименьшие значения функции.
6) Непрерывность функции.
Слайд 8Примеры нахождения обратных функций:
Найти функцию, обратную к функции y=3x+5
б) В этой формуле меняем местами х и у
Ответ: у=1/3(х-5)
2. Найти функцию, обратную к функции у=1/(х-2)
а) х=2+1/у
б) у=2+1/х
Ответ: у=2+1/х
Вывод: область определения и множество значений данной и
обратной функции меняются местами.
Знать: Если функция имеет обратную, то её график симетричен
относительно прямой у=х
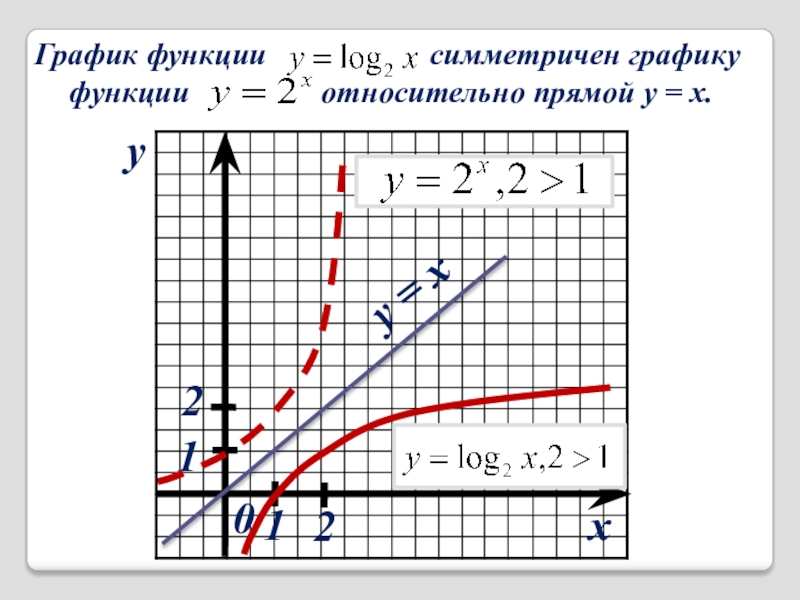
Слайд 9через у
Применим данный алгоритм для нахождения функции, обратной показательной функции
Рассмотрим функцию
D(y) Є R, Е(у)>0
Выразим х через у по определению логарифма х=
Меняем местами х и у и получаем функцию обратную,
показательной: У=
D(y)>0, Е(у) Є R
Слайд 12
Вывод:
Обратную функцию принято
Показательная функция имеет обратную.
Слайд 13x
y
0
1
2
3
1
2
4
8
- 1
- 2
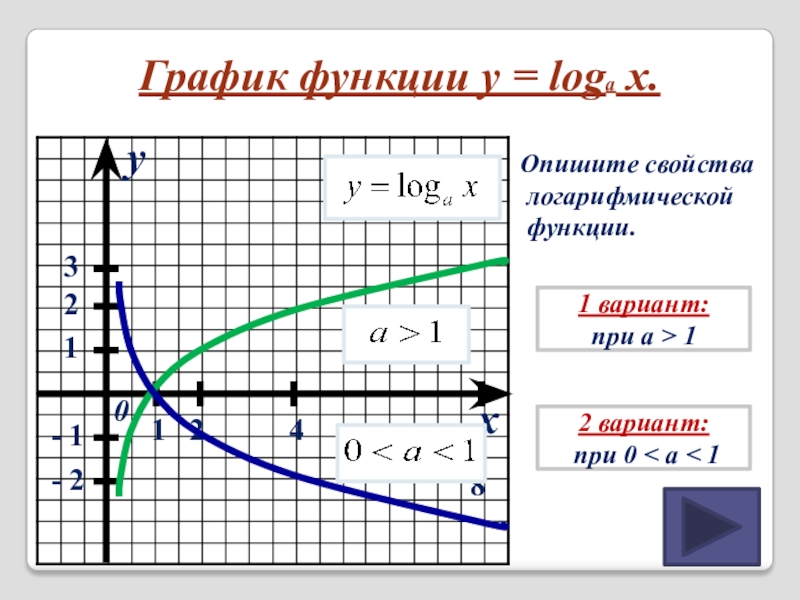
График функции y = loga x.
Опишите свойства
логарифмической
1 вариант:
при a > 1
2 вариант:
при 0 < a < 1
Слайд 14через у
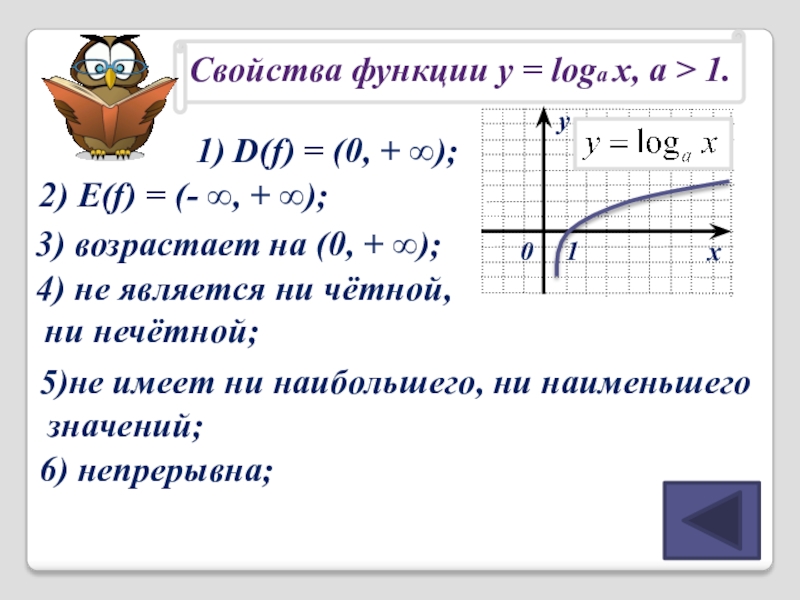
1) D(f) = (0, + ∞);
2) E(f) = (- ∞,
3) возрастает на (0, + ∞);
4) не является ни чётной,
ни нечётной;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
1
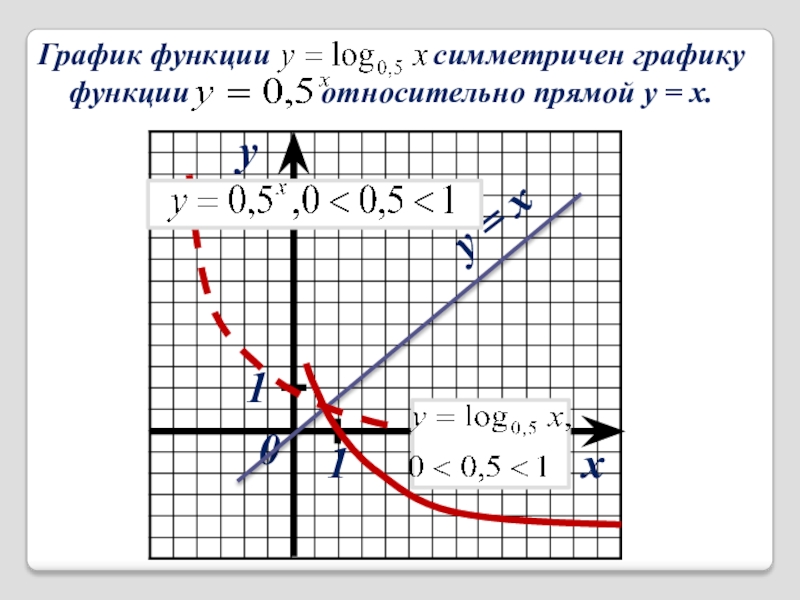
Слайд 15через у
1) D(f) = (0, + ∞);
2) E(f) = (- ∞,
3) убывает на (0, + ∞);
4) не является ни чётной,
ни нечётной;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
1
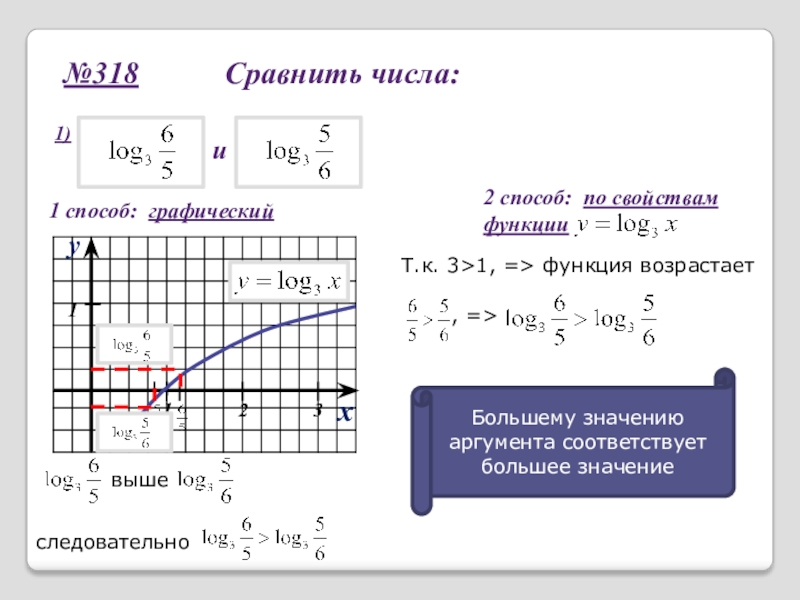
Слайд 16№318 Сравнить числа:
1)
и
1 способ: графический
1
2
3
1
x
y
2 способ:
функции
Т.к. 3>1, => функция возрастает
, =>
Большему значению аргумента соответствует большее значение
выше
следовательно
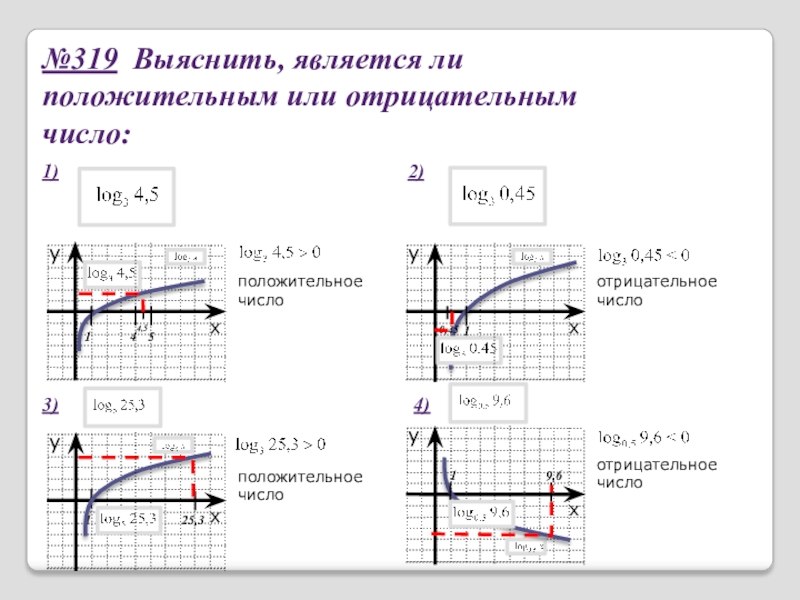
Слайд 17№319 Выяснить, является ли положительным или отрицательным число:
1)
1
5
4
4,5
положительное число
1
0,45
2)
отрицательное число
3)
1
25,3
положительное число
1
9,6
4)
отрицательное
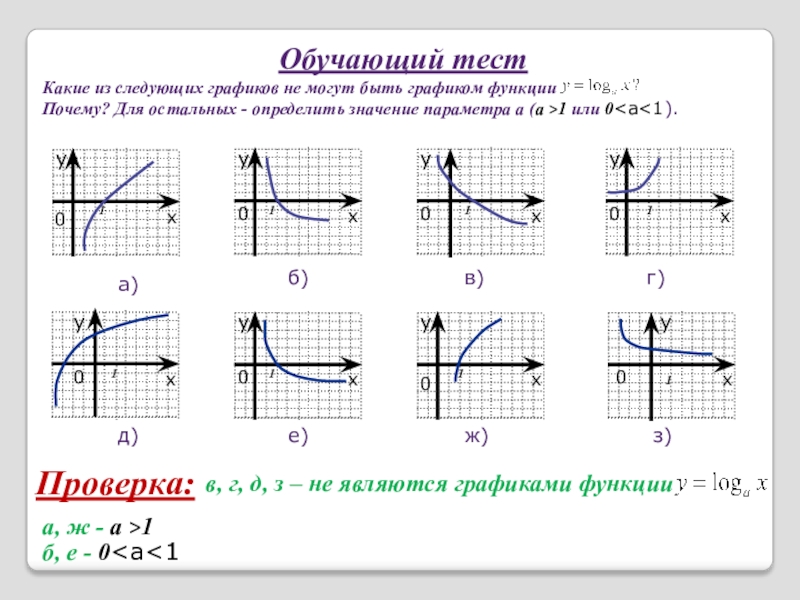
Слайд 18Обучающий тест
Какие из следующих графиков не могут быть графиком функции
0
0
0
0
0
0
0
0
ж)
б)
в)
г)
д)
е)
а)
з)
1
1
1
1
1
1
Проверка:
в, г, д, з – не являются графиками функции
а, ж - а >1
б, е - 0<а<1
1
1
Слайд 19Задача дня
Изобразить схематически график функции:
Решение:
Область определения функции совпадает с решением
На этой области функция задаётся формулой:
Таким образом, график исходной функции совпадает с графиком квадратичной функции при х<2, х≠0;
Слайд 22Список литературы
•Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. Учреждений
• Алгебра и начала анализа: 10 кл. Поурочные планы (по учебнику Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова, Н.Е. Федоровой, М.И. Шабунина) 1 полугодие
Автор-составитель Г.И. Григорьева, 2003.
• Математика 5-11 классы. Коллективный способ обучения. Конспекты уроков, занимательные задачи. Автор-составитель И.В. Фотина, 2009.
•Алгебра и начала математического анализа: дидакт. Материалы для 10 кл. общеобразоват. учреждений: профил. Уровень / [М.И. Шабунин, М.В. Ткачева и др]. – М.: Просвещение, 2008