Сколько двузначных чисел можно составить из цифр:
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок на тему Комбинаторные задачи
Содержание
- 1. Урок на тему Комбинаторные задачи
- 2. Решение Составим таблицу: слева от первого
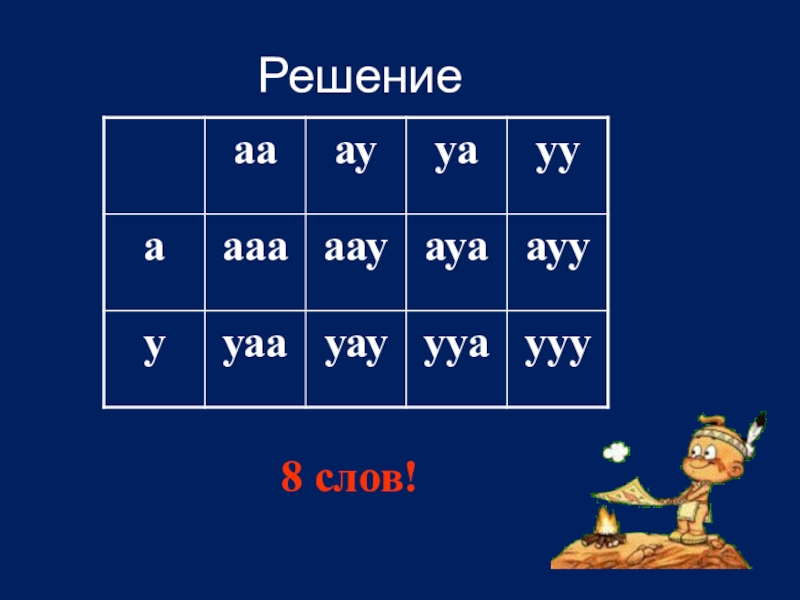
- 3. Второй пример: «В алфавите племени уауа
- 4. Решение 8 слов!
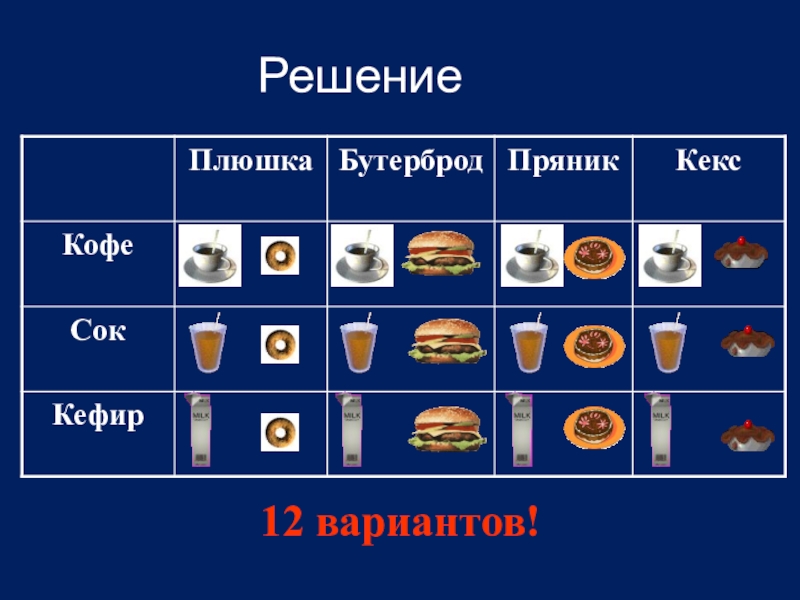
- 5. Третий пример: «На завтрак Вова может выбрать
- 6. Решение 12 вариантов!
- 7. В данных примерах был осуществлен способ перебора
- 8. «Правило умножения» Для того чтобы найти
- 9. Правило умножения для трех, четырех и более
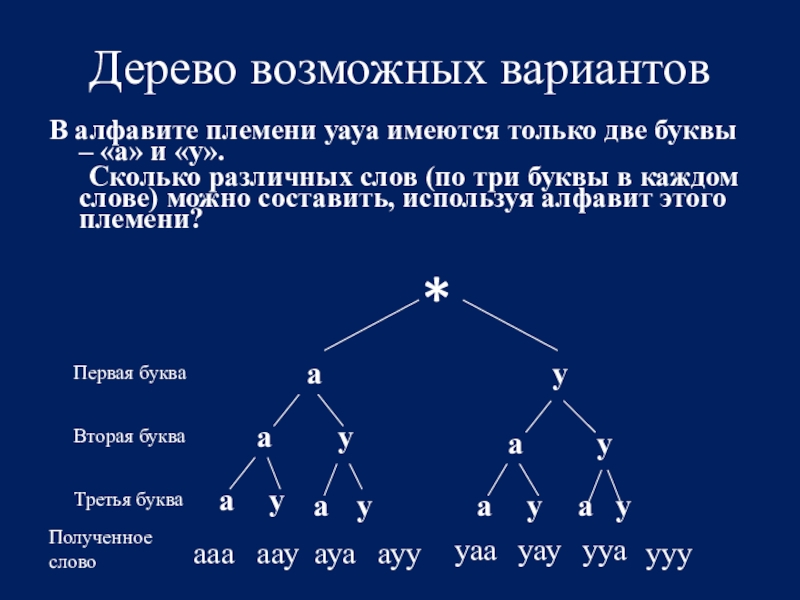
- 10. Дерево возможных вариантов В алфавите племени уауа имеются
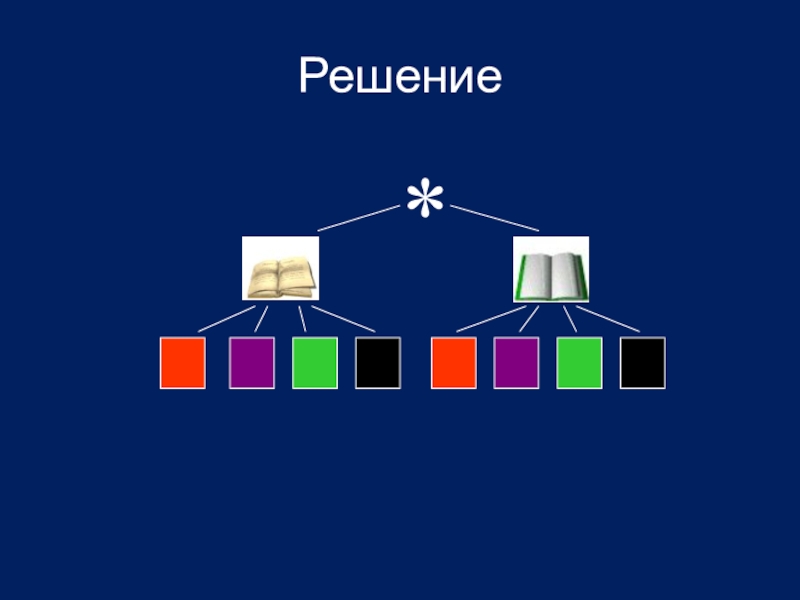
- 11. Задание 1 Имеются ручки четырех цветов: красные, синие,
- 12. Решение *
- 13. Задание 2 Шифр для сейфа составляют из букв
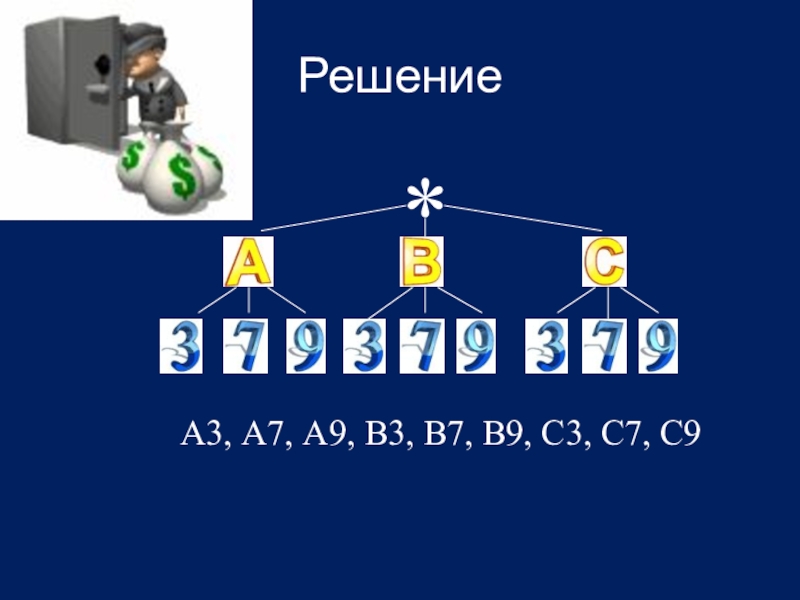
- 14. Решение *А3, А7, А9, В3, В7, В9, С3, С7, С9
- 15. Задание 3 Сколько можно составить различных букетов из
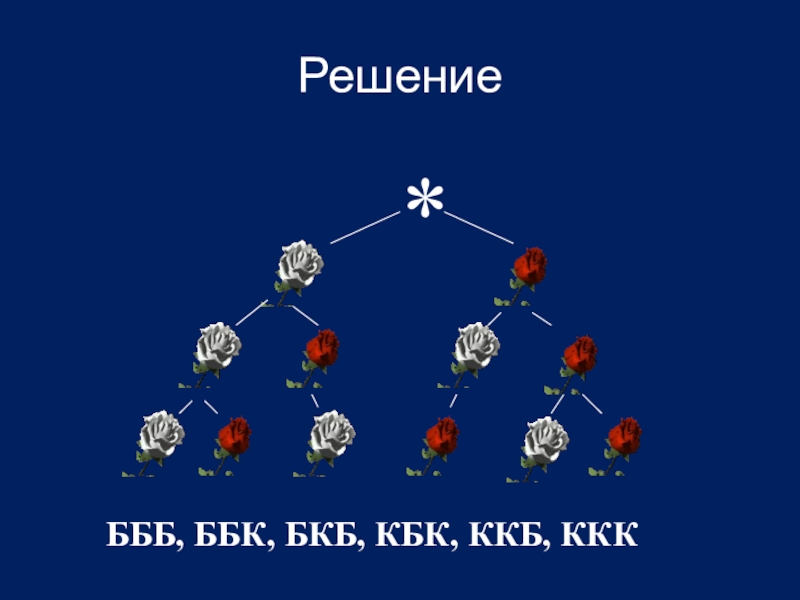
- 16. Решение *БББ, ББК, БКБ, КБК, ККБ, ККК
- 17. Задание 4 Сколькими способами три друга могут
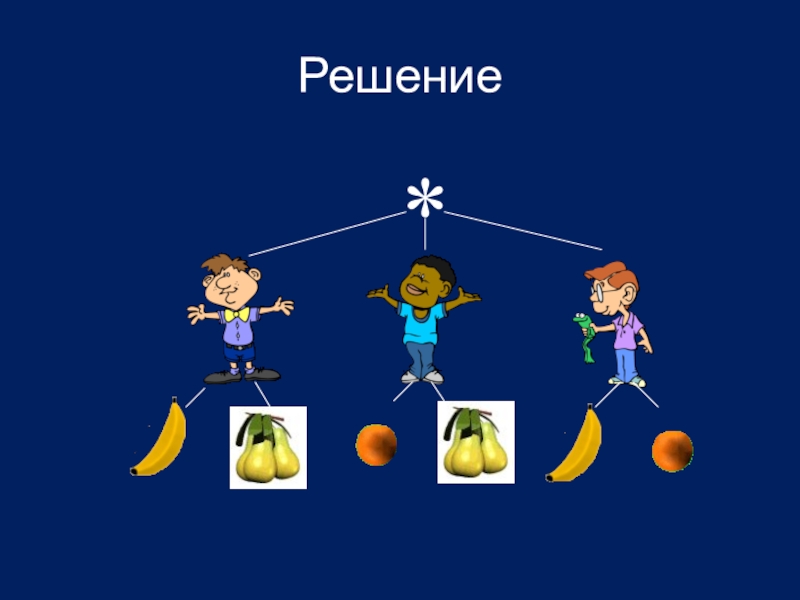
- 18. Решение *
- 19. Слайд 19
- 20. ОпределенияСобытия, которые при данных условиях обязательно происходят,
- 21. Пример 1В коробке лежат 5 конфет в
- 22. Пример 2 В сумке
- 23. 1 задание Среди следующих событий укажите
- 24. 2 заданиеОцените возможность наступления событий, используя для
- 25. 1 задание В три коробки разложили
- 26. Молодцы!
Решение Составим таблицу: слева от первого столбца поместим первые цифры искомых чисел, а выше первой строки – вторые цифры этих чисел.1114174144477174779 чисел!
Слайд 1Перед нами нередко возникают проблемы, которые имеют не одно, а несколько
различных решений. Обычно одни из них нас устраивают, а другие нет.
Рассмотрим первый пример.
Слайд 2 Решение
Составим таблицу: слева от первого столбца поместим первые цифры
искомых чисел, а выше первой строки – вторые цифры этих чисел.
11
14
17
41
44
47
71
74
77
9 чисел!
Слайд 3 Второй пример: «В алфавите племени уауа имеются только две буквы
– «а» и «у».
Сколько различных слов по три буквы в каждом слове можно составить, используя алфавит этого племени?»
Сколько различных слов по три буквы в каждом слове можно составить, используя алфавит этого племени?»
Слайд 5 Третий пример: «На завтрак Вова может выбрать плюшку, бутерброд, пряник или
кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбрать?»
Слайд 7 В данных примерах был осуществлен способ перебора возможных вариантов (возможных комбинаций).
Поэтому
данные задачи называют комбинаторными.
Решения данных задач основывается на общем правиле умножения.
Решения данных задач основывается на общем правиле умножения.
Слайд 8«Правило умножения»
Для того чтобы найти число всех возможных исходов независимого проведения
двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Слайд 9Правило умножения для трех, четырех и более испытаний можно объяснить, не
выходя за рамки плоскости, с помощью геометрической модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна, как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив.
Слайд 10Дерево возможных вариантов
В алфавите племени уауа имеются только две буквы –
«а» и «у».
Сколько различных слов (по три буквы в каждом слове) можно составить, используя алфавит этого племени?
Сколько различных слов (по три буквы в каждом слове) можно составить, используя алфавит этого племени?
*
Первая буква
Вторая буква
Третья буква
Полученное слово
Слайд 11Задание 1
Имеются ручки четырех цветов: красные, синие, зеленые, черные – и
два вида записных книжек. Сколько различных наборов из ручки и записной книжки можно составить из этих предметов?
Слайд 13Задание 2
Шифр для сейфа составляют из букв и цифр, причем на
первом месте всегда ставится буква. Сколько различных вариантов шифра можно составить, используя буквы А, В, С и цифры 3, 7, 9?
Слайд 15Задание 3
Сколько можно составить различных букетов из трех роз, если в
продаже имеются белые и красные розы?
Слайд 17Задание 4
Сколькими способами три друга могут разделить между собой два
банана, две груши и два апельсина так, чтобы каждый получил по два различных фрукта?
Слайд 20Определения
События, которые при данных условиях обязательно происходят, называют достоверными.
События, которые при
данных условиях не могут произойти, называют невозможными.
События, которые при данных условиях имеют равные шансы, называются равновероятными.
События, которые при данных условиях имеют равные шансы, называются равновероятными.
Слайд 21Пример 1
В коробке лежат 5 конфет в синей обертке и одна
в белой. Не глядя в коробку, наугад вынимают одну конфету. Можно ли сказать заранее, какого она будет цвета?
Слайд 22Пример 2
В сумке лежат 4 красных и
4 желтых яблока. Из сумки наугад вынимают яблоко. Какое из событий А, В, С, Д при этом может произойти?
А. Вынуто красное яблоко.
В. Вынуто желтое яблоко.
С. Вынуто зеленое яблоко.
Д. Вынуто яблоко.
А. Вынуто красное яблоко.
В. Вынуто желтое яблоко.
С. Вынуто зеленое яблоко.
Д. Вынуто яблоко.
Слайд 231 задание
Среди следующих событий укажите случайные, достоверные и невозможные.
А.
Попугай научится говорить.
В. Вы садитесь в поезд и доезжаете до Северного полюса.
С. Наугад взятая с полки книга оказывается учебником математики.
Д. В полдень бьют Кремлевские часы.
Е. Вода в Тихом океане закипит.
В. Вы садитесь в поезд и доезжаете до Северного полюса.
С. Наугад взятая с полки книга оказывается учебником математики.
Д. В полдень бьют Кремлевские часы.
Е. Вода в Тихом океане закипит.
Слайд 242 задание
Оцените возможность наступления событий, используя для этого слова: «достоверное событие»,
«случайное событие», «невозможное событие», а также «очень вероятное событие» и «маловероятное событие».
А. Завтра будет хорошая погода.
В. Вас пригласят в гости.
С. В январе в городе пойдет снег.
Д. В 12 часов ночи в городе идет дождь, а через 24 часа будет светить солнце.
Е. На день рождения вам подарят говорящего крокодила.
F. Вам подарят живого крокодила.
G. Вы получите «пятерку» за контрольную работу по математике.
А. Завтра будет хорошая погода.
В. Вас пригласят в гости.
С. В январе в городе пойдет снег.
Д. В 12 часов ночи в городе идет дождь, а через 24 часа будет светить солнце.
Е. На день рождения вам подарят говорящего крокодила.
F. Вам подарят живого крокодила.
G. Вы получите «пятерку» за контрольную работу по математике.
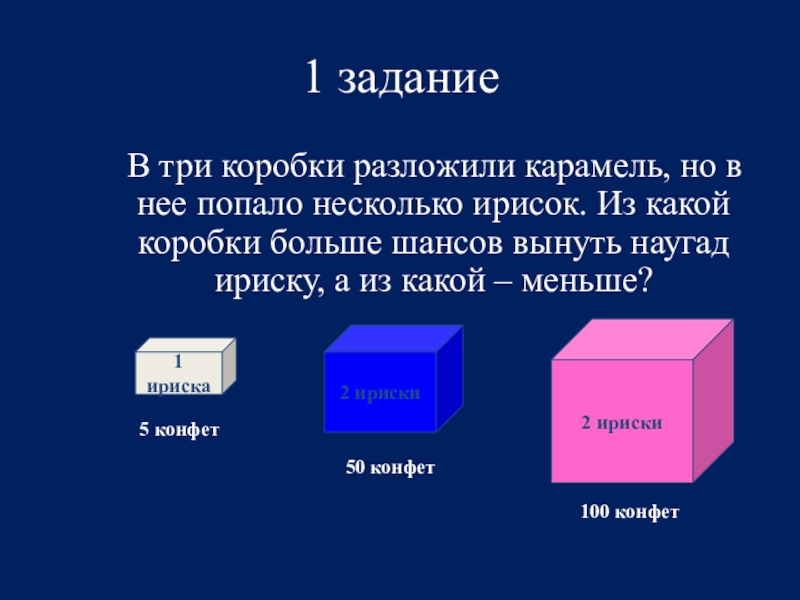
Слайд 251 задание
В три коробки разложили карамель, но в нее
попало несколько ирисок. Из какой коробки больше шансов вынуть наугад ириску, а из какой – меньше?