- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок 1 Рациональные числа
Содержание
- 1. Урок 1 Рациональные числа
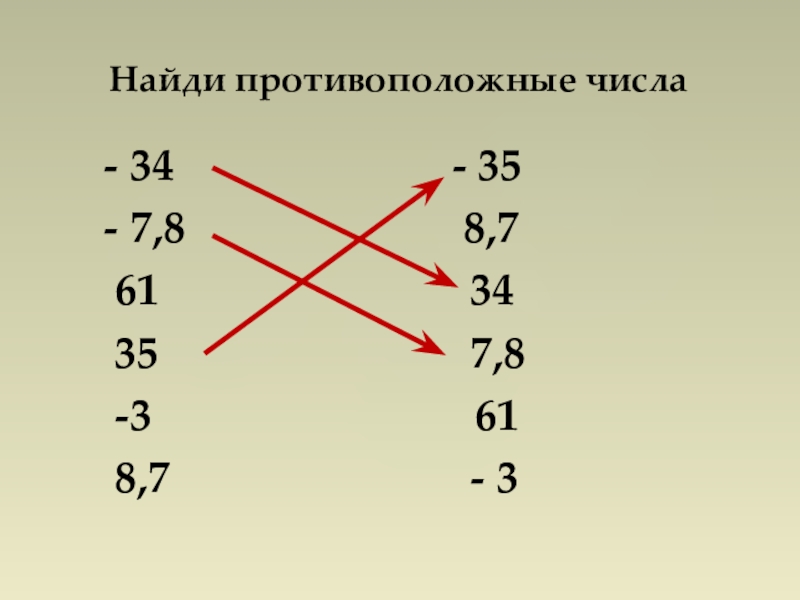
- 2. - 34
- 3. Выполните
- 4. - 12 и - 5
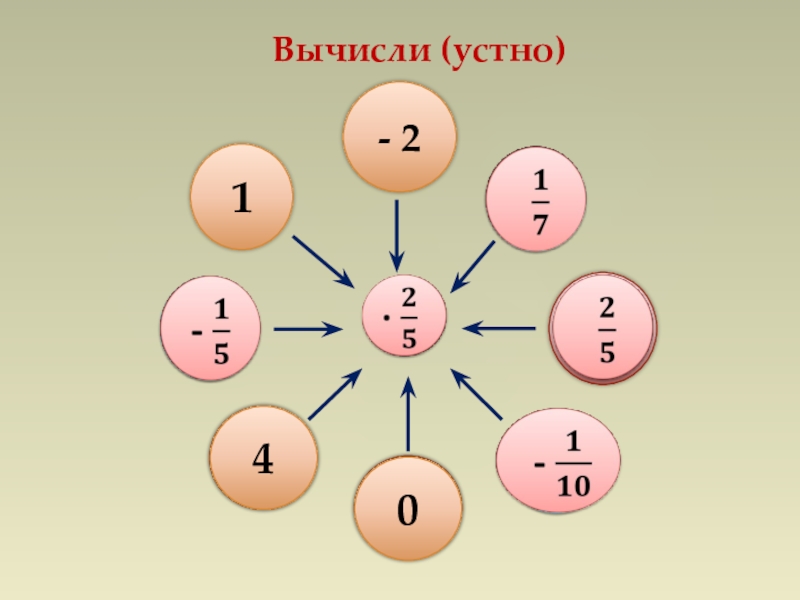
- 5. Вычисли (устно)- 5 1100- 2041
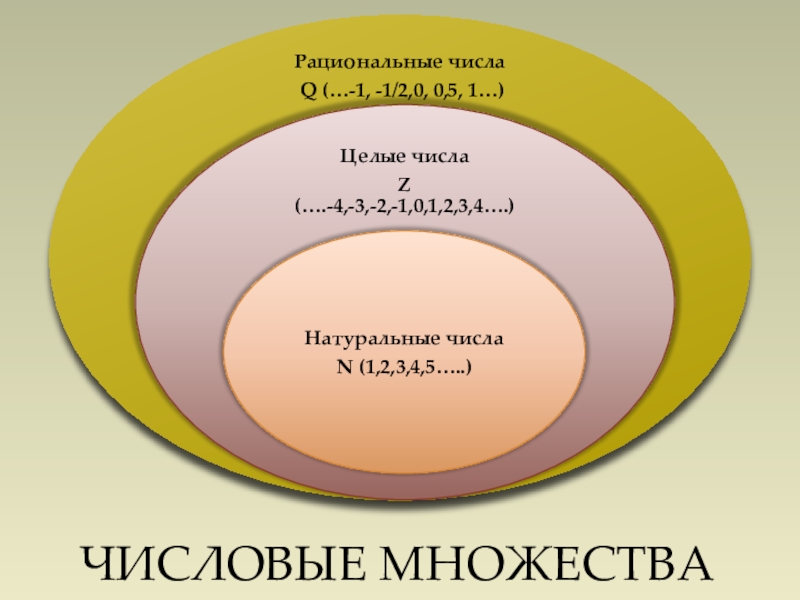
- 6. ЧИСЛОВЫЕ МНОЖЕСТВА
- 7. Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью, числитель — целое число, а знаменатель —натуральное число.Например: ¼.
- 8. Определение:
- 9. Слайд 9
- 10. Не все обыкновенные дроби можно представить в виде десятичной:1/3=0,333..=0,(3)5/11=0,4545…=0,(45)1/15=0,0666…=0,0(6)ПЕРИОДИЧЕСКИЕ ДРОБИ.
- 11. Любое рациональное число можно представить либо в
- 12. Полезно запомнить такое правило:Если в знаменателе обыкновенной
- 13. Сложение рациональных чисел обладает: переместительным
- 14. Умножение рациональных чисел обладает: переместительным,
- 15. Прибавление нуля не изменяет
- 16. изучить п. 37; Решить: № 1196 (а), № 1197 (а), № 1199, № 1200 (а).Домашнее задание
Слайд 1Бачева Татьяна Сергеевна, учитель математики МБОУ «Гимназия №75»
г. Казань,
Республика Татарстан
6 класс
Слайд 3
Выполните умножение и деление целых чисел:
1) -15 · (-4) =
2)
3) -25 · (-3) =
4) 4 ∙ 12 =
5) 18:(-2) =
6) -10 · (-10) =
7) 0: (-40) =
8) 100 : (-5) =
9) -39 : 13 =
10) -80 : (-2) =
Слайд 4 - 12 и - 5
-5 и
3,6 и 7,9
- 2,5 и 3,1
Какие целые числа расположены между данными ?
-6 ; - 7 ; - 8 ; - 9 ; - 10 ; - 11
-1 ; - 2 ; - 3 ; - 4
4 ; 5 ; 6 ; 7
- 2 ; - 1 ; 0 ; 1 ; 2 ; 3
Слайд 7Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью, числитель — целое число, а
Например: ¼.
Слайд 10Не все обыкновенные дроби можно представить в виде десятичной:
1/3=0,333..=0,(3)
5/11=0,4545…=0,(45)
1/15=0,0666…=0,0(6)
ПЕРИОДИЧЕСКИЕ ДРОБИ.
Слайд 11Любое рациональное число можно представить либо в виде конечной десятичной дроби,
ВНИМАНИЕ!
Слайд 12Полезно запомнить такое правило:
Если в знаменателе обыкновенной дроби нет простых множителей,
Если в знаменателе несократимой обыкновенной дроби имеются простые множители, отличные от 2 и 5, то эту дробь можно выразить только бесконечной десятичной дробью.
Как узнать, какой десятичной дробью может быть выражено рациональное число?