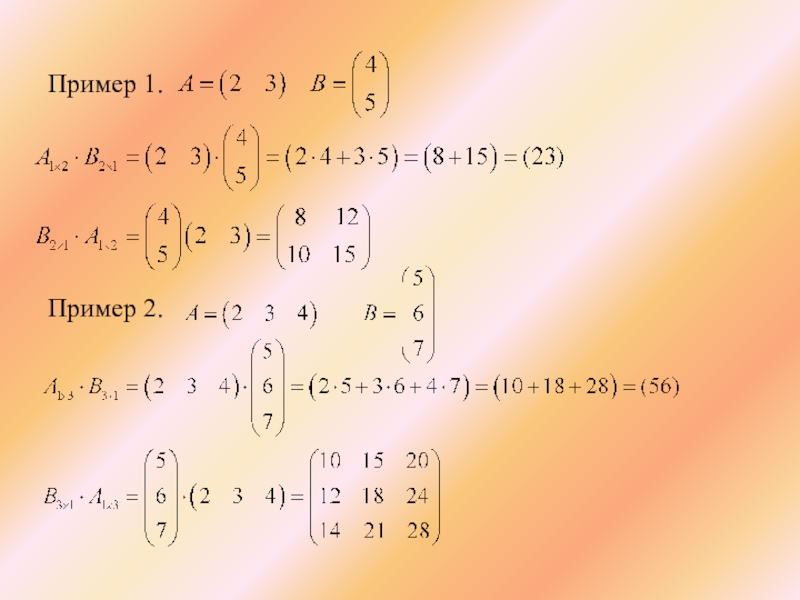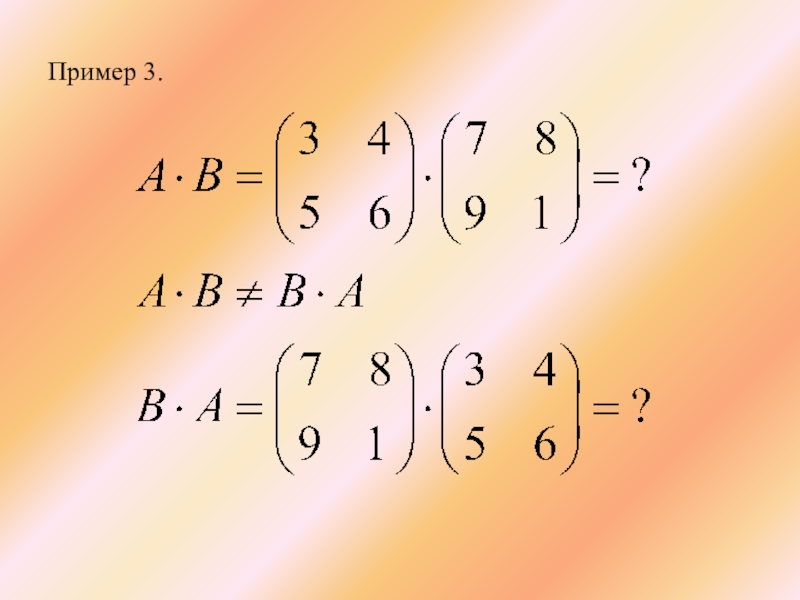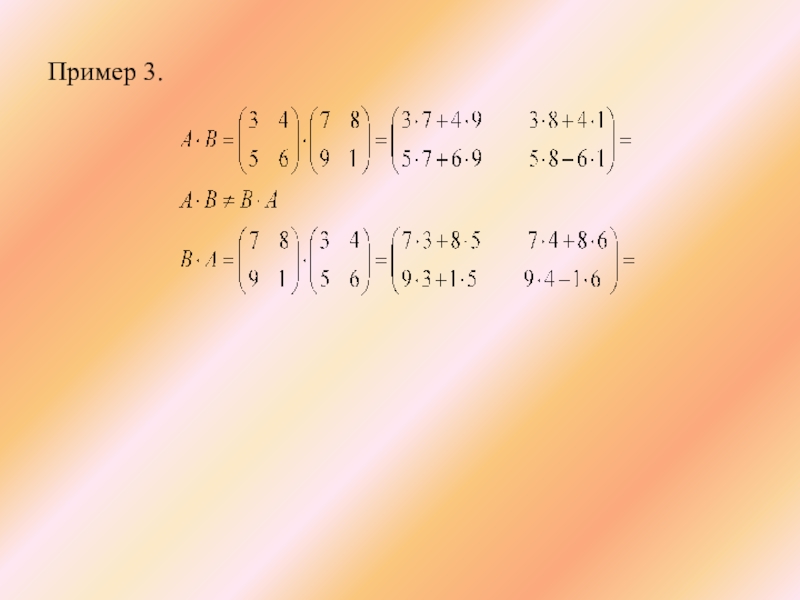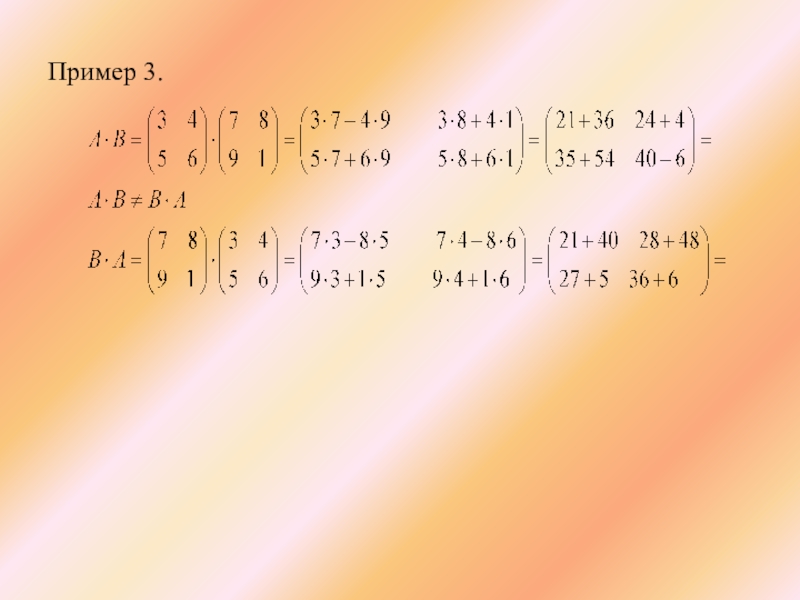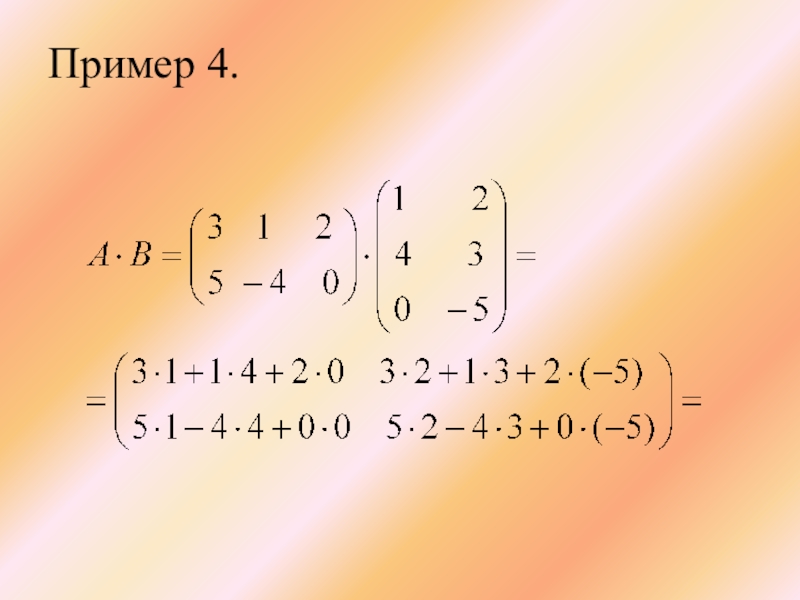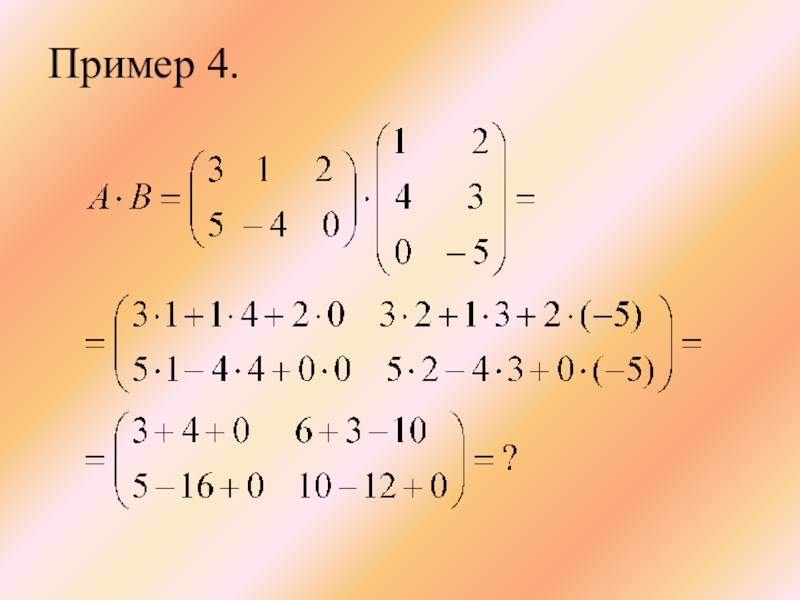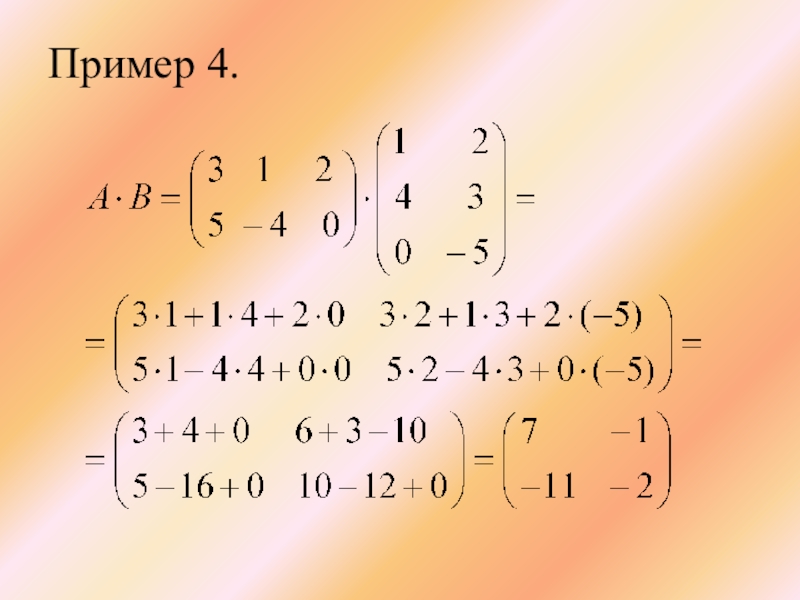- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Умножение матриц
Содержание
- 1. Умножение матриц
- 2. Слайд 2
- 3. Математика является универсальным языком, который широко применяется
- 4. Историческая справка
- 5. Ключевые понятия и термины:матрица;определитель матрицы;квадратная матрица;прямоугольная матрица;виды матриц.
- 6. Литература 1. Алгебра и начала математического анализа:
- 7. Вопросы к темеЧто такое матрицы и
- 8. Свойства сложения и умножения матриц.
- 9. Произведением двух матриц АВ является
- 10. Свойства произведений матриц
- 11. Пример 1. Пример 2.
- 12. Пример 3.
- 13. Пример 3.
- 14. Пример 3.
- 15. Пример 3.
- 16. Решаем на доске и в тетрадяхПример 4.
- 17. Пример 4.
- 18. Пример 4.
- 19. Пример 4.
- 20. Переместительный закон умножения в общем случае не
- 21. Где ещё применяются матрицы? На занятии по математике?
- 22. Где ещё применяются матрицы?Таблица умножения – это
- 23. Где ещё применяются матрицы?Таблица умножения?
- 24. Где ещё применяются матрицы?Таблица умножения –Необходимо установить
- 25. Где ещё применяются матрицы?Таблица умножения – это
- 26. Где ещё применяются матрицы?Таблица умножения – это
- 27. Где ещё применяются матрицы?Таблица умножения – это
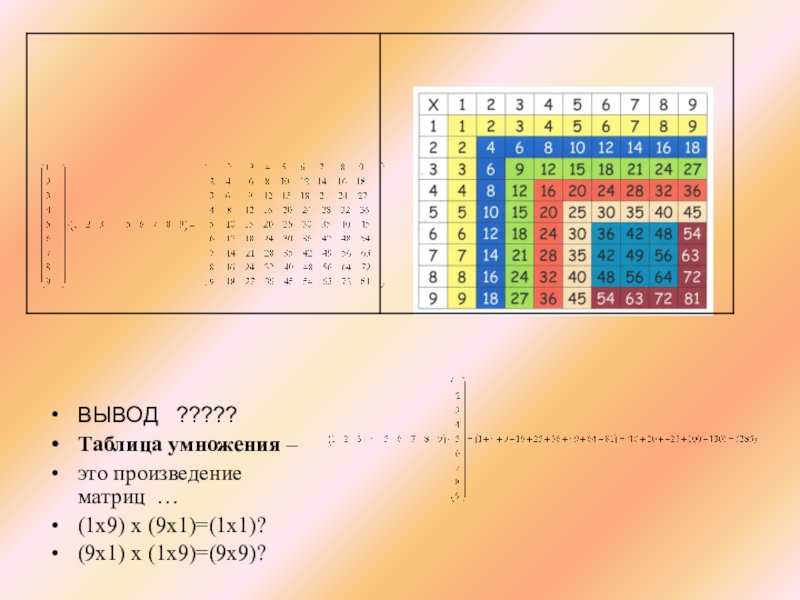
- 28. ВЫВОД ?????Таблица умножения – это произведение матриц …(1х9) х (9х1)=(1х1)? (9х1) х (1х9)=(9х9)?
Математика является универсальным языком, который широко применяется во всех сферах человеческой деятельности. Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц. Актуальность этой темы
Слайд 3
Математика является универсальным языком, который широко применяется во всех сферах человеческой
деятельности.
Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц.
Актуальность этой темы усиливается в связи
с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц.
Актуальность этой темы усиливается в связи
с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Слайд 5Ключевые понятия и термины:
матрица;
определитель матрицы;
квадратная матрица;
прямоугольная матрица;
виды матриц.
Слайд 6Литература
1. Алгебра и начала математического анализа: учебник для общеобразоват. организаций:
базов. и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – М.: Просвещение, 2016. – 463 с.
2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с.
3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с.
3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
Слайд 7
Вопросы к теме
Что такое матрицы и зачем они нужны? Какие
виды матриц существуют?
Как найти определитель матрицы?
Какие операции можно выполнять над матрицами?
Как найти определитель матрицы?
Какие операции можно выполнять над матрицами?
Слайд 9
Произведением двух матриц АВ является матрица С, элемент
которой равен сумме произведений соответствующих элементов i - той строки матрицы А и j - того столбца матрицы В. (Чтобы получить i-тую строку произведения, необходимо умножить i-тую строку матрицы А на каждый столбец матрицы В)
Чтобы умножать матрицы, необходимо, чтобы количество столбцов матрицы А было равно количеству строк матрицы В.
Размер А: m×n; размер В: n×p, то размер АВ: m×p.
Чтобы умножать матрицы, необходимо, чтобы количество столбцов матрицы А было равно количеству строк матрицы В.
Размер А: m×n; размер В: n×p, то размер АВ: m×p.
Слайд 20
Переместительный закон умножения в общем случае не имеет смысла, т.е.
. Матрицы, для которых переместительный закон справедлив, называют переместительными.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если, , то
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если, , то
Слайд 22Где ещё применяются матрицы?
Таблица умножения – это произведение матриц
(1 2 3 4 5 6 7 8 9) × (1 2 3 4 5 6 7 8 9) Т или произведение матриц (1 2 3 4 5 6 7 8 9) Т ×(1 2 3 4 5 6 7 8 9)?
Необходимо установить размерность каждой матрицы.
Необходимо установить размерность каждой матрицы.
Слайд 24Где ещё применяются матрицы?
Таблица умножения –Необходимо установить размерность каждой матрицы. В
1 случае это (1х9) х (9х1)=(1х1). Во втором (9х1) х (1х9)=(9х9). Какой вывод вы сделаете? Произведение матрицы строки на матрицу столбец или матрицы столбца на матрицу строку?
Слайд 25Где ещё применяются матрицы?
Таблица умножения – это произведение матриц
(1 2 3 4 5 6 7 8 9) ×(1 2 3 4 5 6 7 8 9) Т или произведение матриц (1 2 3 4 5 6 7 8 9)Т ×(1 2 3 4 5 6 7 8 9)? Необходимо установить размерность каждой матрицы. В 1 случае это (1х9) х (9х1)=(1х1). Во втором (9х1) х (1х9)=(9х9). Какой вывод вы сделаете? Произведение матрицы строки на матрицу столбец или матрицы столбца на матрицу строку?
Слайд 26Где ещё применяются матрицы?
Таблица умножения – это произведение матриц
(1 2
3 4 5 6 7 8 9) ×(1 2 3 4 5 6 7 8 9) Т. ???
В 1 случае это (1х9) х (9х1)=(1х1). Что получили? Сумма или произведение ? Какие числа?
В 1 случае это (1х9) х (9х1)=(1х1). Что получили? Сумма или произведение ? Какие числа?
Слайд 27Где ещё применяются матрицы?
Таблица умножения – это произведение матриц
(1 2
3 4 5 6 7 8 9)Т ×(1 2 3 4 5 6 7 8 9) ? ? ?
Во втором (9х1) х (1х9)=(9х9). Какой вывод вы сделаете?
Во втором (9х1) х (1х9)=(9х9). Какой вывод вы сделаете?
Слайд 28
ВЫВОД ?????
Таблица умножения –
это произведение матриц …
(1х9) х (9х1)=(1х1)?
(9х1) х (1х9)=(9х9)?