- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теория: Исследование функции с помощью производной
Содержание
- 1. Теория: Исследование функции с помощью производной
- 2. Содержание1) Область определения функции2) Свойства функции (четность,
- 3. Область определения функцииОпределение. Областью определения функции называется множество значений независимой переменной, при которых функция определена.Примеры.У= ln(x+1)
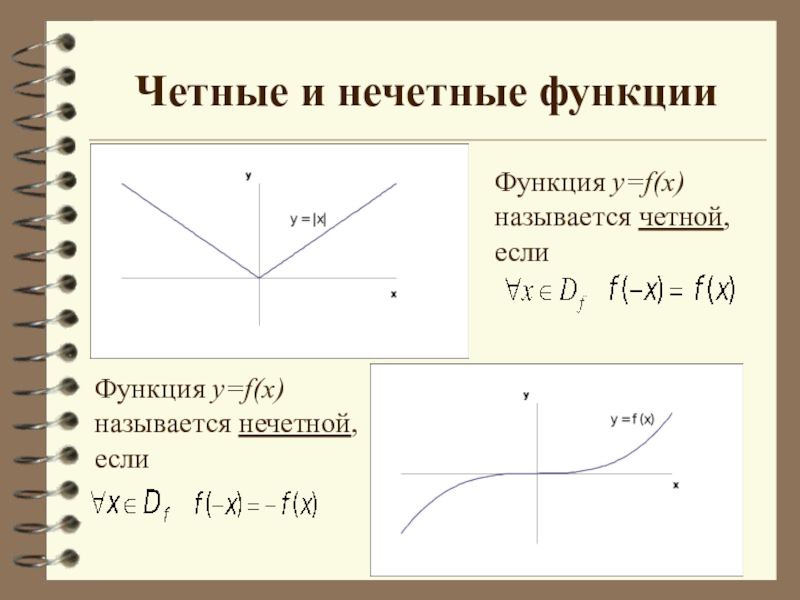
- 4. Четные и нечетные функцииФункция y=f(x) называется четной, еслиФункция y=f(x) называется нечетной, если
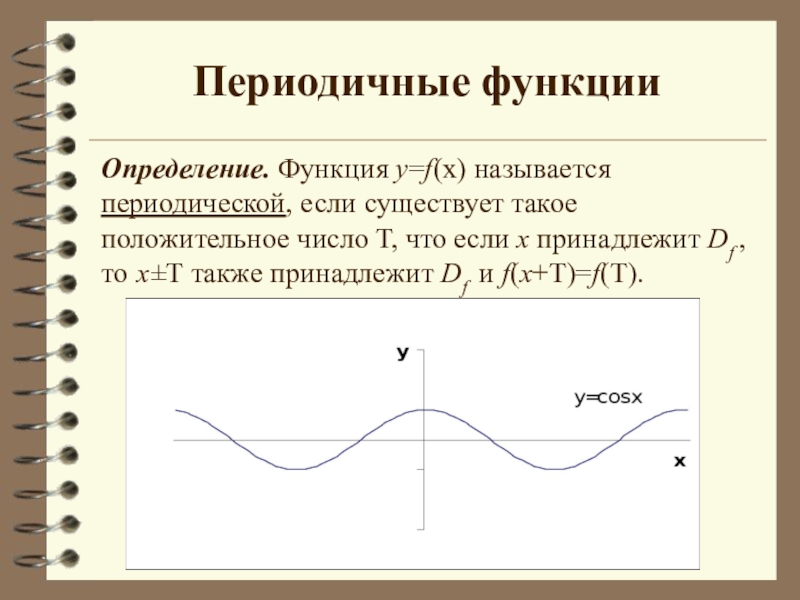
- 5. Периодичные функцииОпределение. Функция y=f(x) называется периодической, если
- 6. Точки пересечения с осями координат
- 7. Непрерывность Характер точек разрыва
- 8. Точки разрыва функцииОпределение. Точкой разрыва функции называется
- 9. Классификация точек разрыва Точки устранимого разрываЕсли в
- 10. Классификация точек разрыва Точки скачка Если
- 11. Классификация точек разрыва Точки разрыва II рода
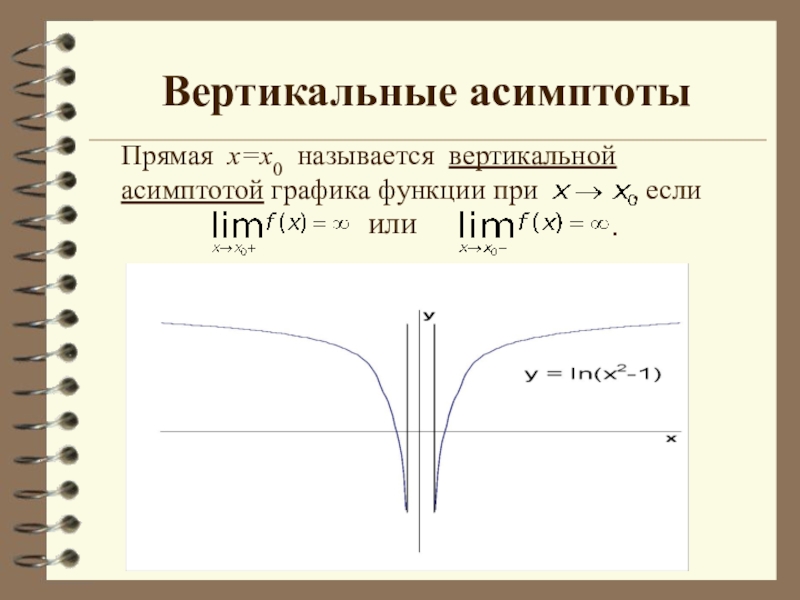
- 12. Вертикальные асимптотыПрямая х=х0 называется вертикальной асимптотой графика
- 13. Наклонные асимптоты Если существует прямая y=kx+b такая,
- 14. Экстремумы функции Пусть
- 15. Исследование функции на монотонностьКритические точки функции х=±1. f '(x)>0 при х1; f '(x)
- 16. Выпуклость функции Функция у=f(х),
- 17. Выпуклость функции. Точки перегиба
- 18. Достаточные условия выпуклости функции и существования точек
- 19. Спасибо за внимание
Слайд 2Содержание
1) Область определения функции
2) Свойства функции (четность, нечетность, периодичность)
4) Точки пересечения
5) Непрерывность функции. Характер точек разрыва
6) Асимптоты
7) Экстремумы функции. Исследование функции на монотонность
8) Выпуклость функции. Точки перегиба
Слайд 3Область определения функции
Определение. Областью определения функции называется множество значений независимой переменной,
Примеры.
У= ln(x+1)
Слайд 4Четные и нечетные функции
Функция y=f(x) называется четной, если
Функция y=f(x) называется нечетной,
Слайд 5Периодичные функции
Определение. Функция y=f(x) называется периодической, если существует такое положительное число
Слайд 6Точки пересечения с осями координат
При исследовании функции
Абсциссы точек пересечения графика функции с осью Ох находятся из системы уравнений у=f(x) и у=0, а ординаты точек пересечения графика функции с осью Оу находятся из системы уравнений у=f(x) и х=0.
Слайд 7Непрерывность
Характер точек разрыва
Функция у=f(x) называется непрерывной в
Функции, непрерывные в каждой точке из области определения функции, называются непрерывными функциями.
Примеры непрерывных функций: y=cosx, y=sinx, y=ex , y=Pn(x) (многочлен степени n).
Слайд 8Точки разрыва функции
Определение. Точкой разрыва функции называется точка из области определения
Пример. Функция
разрывна в 0, так как
Слайд 9Классификация точек разрыва
Точки устранимого разрыва
Если в точке х0 существуют конечные односторонние
Слайд 10Классификация точек разрыва
Точки скачка
Если в точке х0 существуют конечные
Слайд 11Классификация точек разрыва
Точки разрыва II рода
Если хотя бы один
Слайд 12Вертикальные асимптоты
Прямая х=х0 называется вертикальной асимптотой графика функции при
или
.
Слайд 13Наклонные асимптоты
Если существует прямая y=kx+b такая, что
, то эта
асимптотой графика функции f при
.
Для того чтобы прямая y=kx+b была асимптотой, необходимо и достаточно, чтобы выполнялись следующие условия:
,
.
Слайд 14Экстремумы функции
Пусть функция f (x) определена
Точки минимума и точки максимума функции называются точками экстремума функции.
Необходимое условие экстремума. Пусть точка х0 - точка экстремума функции. Тогда либо производная функции в этой точке равна 0, либо не существует.
Слайд 15Исследование функции на монотонность
Критические точки функции х=±1. f '(x)>0 при х
функция возрастает
функция убывает
Известно, что если f '(x)>0 (f '(x)>0) в (а, b), то функция f (x) строго возрастает (строго убывает) в (а, b).
Рассмотрим функцию f(x) = x + 1|x
Слайд 16Выпуклость функции
Функция у=f(х), определенная на интервале (а,
Слайд 17Выпуклость функции.
Точки перегиба
Если график функции в
Также говорят, что график функции f (x) имеет на интервале (a, b) выпуклость, направленную вниз (вверх), если график этой функции в пределах (a, b) лежит не ниже (не выше) любой своей касательной.
Слайд 18Достаточные условия выпуклости функции и существования точек перегиба
Достаточное
Если на интервале (а,b) f ''(x)>0, то на интервале (а,b) функция выпукла вниз, и если на интервале f ''(x)<0, то
на интервале (а,b) функция выпукла вверх.
Достаточное условие строгой выпуклости функции
Если в левой и правой полуокрестностях некоторой точки х0 f ''(x) имеет противоположные знаки, то точка х0 – точка перегиба функции.