Дарья
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Совершенствование техники устного счета Презентация
Содержание
- 1. Совершенствование техники устного счета Презентация
- 2. Задачи:Найти как можно больше новых и необычных
- 3. ВступлениеЧеловеку в повседневной жизни невозможно обойтись без
- 4. При изучении темы меня заинтересовали следующие вопросы:
- 5. Актуальность темыУстный счет – гимнастика для ума.
- 6. Те способы вычислений, которыми мы пользуемся сейчас,
- 7. Умножение на пальцах Древнерусский способ умножения на
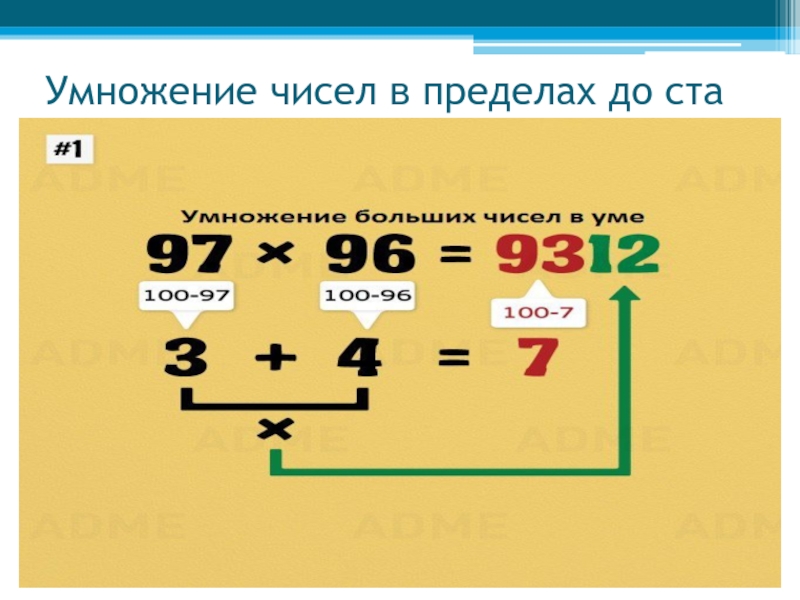
- 8. Умножение чисел в пределах до ста
- 9. Умножение для числа 9 Растопырьте пальцы на
- 10. Допустим, хотим умножить 9 на 6. Загибаем
- 11. Умножение на 25 Чтобы умножить какое-нибудь число,
- 12. Умножения на 125Умножения на 125 – это
- 13. Умножения чисел, оканчивающихся на 5, самих на
- 14. Умножение на 11Пусть надо умножить 27 *
- 15. Способы быстрого сложения и вычитания натуральных чиселЕсли
- 16. Взведение в квадрат чисел, оканчивающихся на 5
- 17. Признаки делимости С признаками делимости мы впервые
- 18. Признак делимости на 4Число делится на 4,
- 19. Признак делимости на 19 Зачеркни последнюю цифру,
- 20. ЗаключениеМы вступили в новое тысячелетие! Грандиозные открытия
- 21. Использованные ресурсыhttp://global-katalog.ru/item10719.htmlhttp://www.slideboom.comhttp://nsportal.ruУстный счет/Сост. П.М.Камаев. – М.: Чистые
Задачи:Найти как можно больше новых и необычных способов вычислений.Научиться применять их на практикеВыбрать для себя самые интересные и удобные в использовании
Слайд 1Актуальность и оптимизация использования техники вычислительного счета
Выполнила ученица 7 класса «А»
Смердова
Слайд 2Задачи:
Найти как можно больше новых и необычных способов вычислений.
Научиться применять их
на практике
Выбрать для себя самые интересные и удобные в использовании
Выбрать для себя самые интересные и удобные в использовании
Слайд 3Вступление
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках
математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
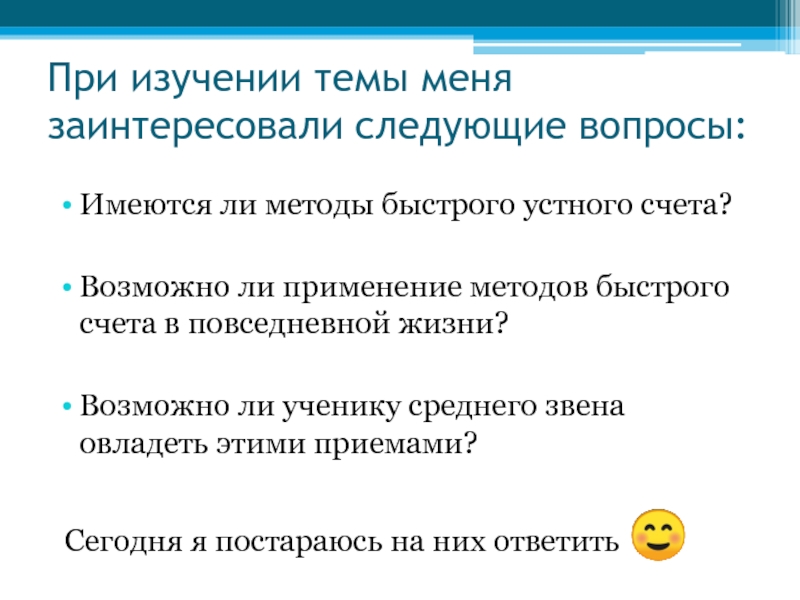
Слайд 4При изучении темы меня заинтересовали следующие вопросы:
Имеются ли методы быстрого устного
счета?
Возможно ли применение методов быстрого счета в повседневной жизни?
Возможно ли ученику среднего звена овладеть этими приемами?
Сегодня я постараюсь на них ответить ☺
Возможно ли применение методов быстрого счета в повседневной жизни?
Возможно ли ученику среднего звена овладеть этими приемами?
Сегодня я постараюсь на них ответить ☺
Слайд 5Актуальность темы
Устный счет – гимнастика для ума. Счет в уме является
самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы естественно-математического цикла. Умножение без калькулятора – тренировка памяти и математического мышления. Вычислительная техника совершенствуется и по сей день, но любая машина делает то, что в нее закладывают люди, а мы узнали некоторые приемы устного счета, которые помогут нам в жизни.
Слайд 6Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так
просты и удобны. В старину пользовались более громоздкими и медленными приемами. Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления – приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей.
Слайд 7Умножение на пальцах
Древнерусский способ умножения на пальцах является одним из наиболее
распространённых методов, которым успешно пользовались на протяжении многих столетий. Они научились умножать на пальцах числа от 6 до 9.
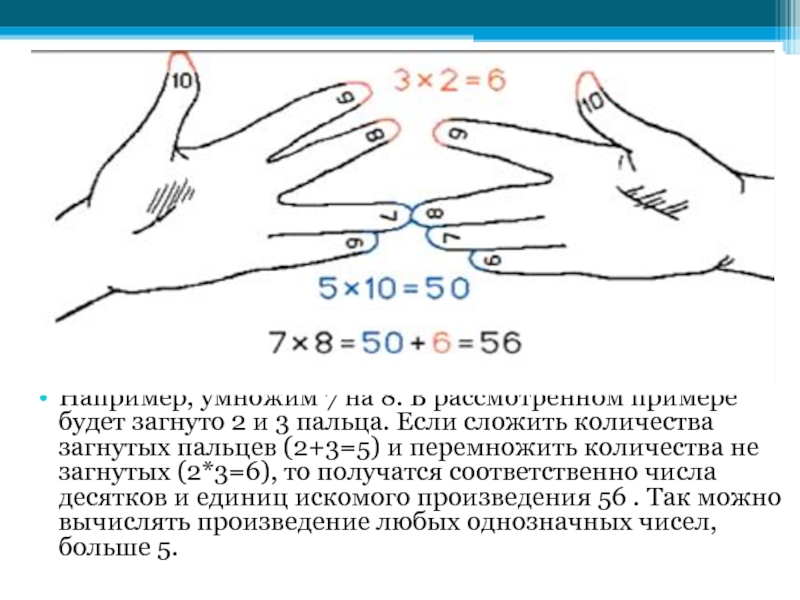
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2*3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2*3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
Слайд 9Умножение для числа 9
Растопырьте пальцы на обеих руках и поверните руки
ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Слайд 10Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным
числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9*6=54
Слайд 11Умножение на 25
Чтобы умножить какое-нибудь число, нужно данное число разделить 4.
Ответ - полные сотни, остаток – неполные (1, 2, 3 или 25, 50, 75).
Например 135*25=(135:4=100:4+35:4)=33 сотни, остаток 3 (или неполная сотня – 75)=3375.
Например 135*25=(135:4=100:4+35:4)=33 сотни, остаток 3 (или неполная сотня – 75)=3375.
Слайд 12Умножения на 125
Умножения на 125 – это деление на 8 и
умножение на 1000
Например:
42 * 125 = 88 : 8 * 1000 = 11 000
Например:
42 * 125 = 88 : 8 * 1000 = 11 000
Слайд 13Умножения чисел, оканчивающихся на 5, самих на себя
Например:
35 х 35 =
3 х 4 и приписываем 5 х 5, т.е. 35 х 35 = 1225
Слайд 14Умножение на 11
Пусть надо умножить 27 * 11. Достаточно сложить эти
две цифры 2 + 7 = 9, поставить итог между ними и мы получим ответ 27 * 11 = 297. При сложении, разумеется, может получиться начинающееся с 1 двузначное число. Тогда эту единицу надо прибавить к цифре десятков, а в середину вставлять только цифру единиц суммы.
Например, 85*11; 8 + 5=13.
Значит, 85 * 11 = (8 + 1) | | 35 = 935.
Значит, 85 * 11 = (8 + 1) | | 35 = 935.
Слайд 15Способы быстрого сложения и вычитания натуральных чисел
Если одно из слагаемых увеличить
на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится.
Например: 762+639=(762+8)+(639-8)=770 + 631=1401
Например: 762+639=(762+8)+(639-8)=770 + 631=1401
Слайд 16Взведение в квадрат чисел, оканчивающихся на 5
Для того чтобы возвести в
квадрат число оканчивающееся на 5, надо найти значение выражения 100*количество десятков числа*(количество десятков+1)+25.
Например 185 в квадрате=100*18*(18+1)+25=34225.
Например 185 в квадрате=100*18*(18+1)+25=34225.
Слайд 17Признаки делимости
С признаками делимости мы впервые встречаемся в 5 классе. По
программе нас знакомят только с некоторыми из них – на 2, 3, 5, 9, 10. А признаки делимости помогают очень быстро выяснять, делится ли данное число например, на 2, 3 или 5. Однако я узнала, что существуют признаки делимости и на другие числа.
Слайд 18Признак делимости на 4
Число делится на 4, если две последние его
цифры нули или образуют число, делящееся на 4. В остальных случаях число на 4 не делится.
Например:
31700 делится на 4, так как оканчивается двумя нулями;
215634 не делится на 4, так как последние две цифры дают число 34, не делящееся на 4;
16628 делится на 4, так как две последние цифры дают число 28, делящееся на 4.
Например:
31700 делится на 4, так как оканчивается двумя нулями;
215634 не делится на 4, так как последние две цифры дают число 34, не делящееся на 4;
16628 делится на 4, так как две последние цифры дают число 28, делящееся на 4.
Слайд 19Признак делимости на 19
Зачеркни последнюю цифру, удвой её, прибавь к оставшемуся
числу, проверяй да или нет.
Например возьмём число 3245
324+5*2=334
33+4*2=41 – не делится на 19, значит, 3245 не делится на 19.
Или возьмём число 1292
129+2*2=133
13+3*2=19 – делится на 19, значит, 1292 делится на 19
Например возьмём число 3245
324+5*2=334
33+4*2=41 – не делится на 19, значит, 3245 не делится на 19.
Или возьмём число 1292
129+2*2=133
13+3*2=19 – делится на 19, значит, 1292 делится на 19
Слайд 20Заключение
Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы
много знаем, многое умеем. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д.н.э.- Пифагора- «Всё есть число!». Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попыталась показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись. В заключении хочу отметить, что устный счёт развивает память, интерес к математике, логическое мышление, расширяет кругозор учащихся в области математических знаний
Слайд 21Использованные ресурсы
http://global-katalog.ru/item10719.html
http://www.slideboom.com
http://nsportal.ru
Устный счет/Сост. П.М.Камаев. – М.: Чистые пруды, 2007- Библиотечка «Первого
сентября», серия «Математика». Вып. 3(15).
Глейзер Г.И. История математики в школе. – М.,1981
Глейзер Г.И. История математики в школе. – М.,1981