красногвардейского района
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение комбинаторных задач ( 6 класс)
Содержание
- 1. Решение комбинаторных задач ( 6 класс)
- 2. Основатели «Теории вероятности»П.Ферма Я. Бернулли
- 3. Понятие Элементарные события
- 4. Схема решения задач1. Определить, что является элементарным
- 5. Типы задачI. Задачи, где можно выписать все
- 6. Правило.Если при одном подбрасывании монеты всего
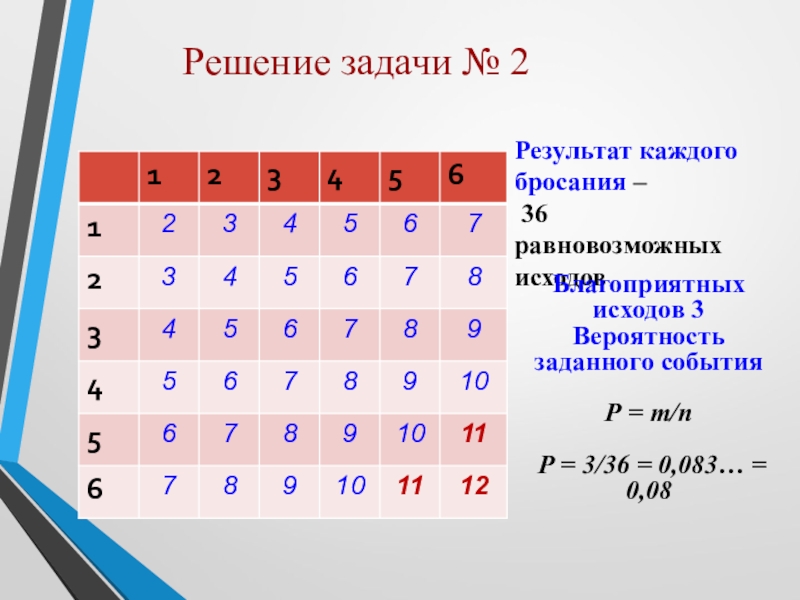
- 7. Задача №2. В случайном эксперименте бросают две
- 8. Решение задачи № 2Результат каждого бросания –
- 9. II.Задачи, где все элементарные события выписывать сложно,но
- 10. Решение задачи № 3Обратить внимание! (первым, вторым, седьмым –не важно!)n=2+2+4=8m=2 (благоприятные исходы-испанцы 2 человека)Р = 2/8=0,25
- 11. III.Использование формулы вероятности противоположного события.Р(А‾) +Р(А) =1В
- 12. Решение задачи №4:На стенде испытаний – 500
- 13. Задача №4.2Вероятность того, что новая шариковая ручка
- 14. Решение задачи №4.21.Определим событие А – выбранная
- 15. IV. Задачи, где искомые значения не выводятся из текста.Обратить внимание! n!=1•2•3•4 • … •n0!=1Cn ª=n!/а!(n-а)!
- 16. Задача №5В группе из 20 студентов надо
- 17. Решение задачи № 5С20²=20!/2!(20-2)! = 20 •19
- 18. Литература:«Вероятность и статистика. 5-9 классы.» Е.А. Бунимович,
- 19. Сайты:Материалы с сайта www.1september.ru, фестиваль педагогических идей «Открытый урок»Материалы с сайта www.mathege.ru
Основатели «Теории вероятности»П.Ферма Я. Бернулли Х. Гюйгенс Б. Паскаль «Вероятность – возможность исполнения, осуществимости чего-нибудь».
Слайд 1Решение задач по теории вероятностей
Федорова Людмила Александровна
учитель математики ГБОУ СОШ №182
Слайд 2
Основатели
«Теории вероятности»
П.Ферма
Я. Бернулли
Х. Гюйгенс
Б. Паскаль
«Вероятность –
возможность исполнения, осуществимости чего-нибудь».
Слайд 3Понятие
Элементарные события (элементарные исходы) , опыта-
простейшие события, которыми может окончиться случайный опыт.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Слайд 4Схема решения задач
1. Определить, что является элементарным событием (исходом) в данном
случайном эксперименте (опыте)
2.Найти общее число элементарных событий (n)
3.Определить, какие элементарные события благоприятствуют интересующему нас событию А, найти их число (m)
4. Найти вероятность события А по формуле Р(А) = т/п
2.Найти общее число элементарных событий (n)
3.Определить, какие элементарные события благоприятствуют интересующему нас событию А, найти их число (m)
4. Найти вероятность события А по формуле Р(А) = т/п
Слайд 5Типы задач
I. Задачи, где можно выписать все элементарные события эксперимента.
Задача №1.
В
случайном эксперименте подбрасывают симметричную монету. Какова вероятность выпадения решки?
Решение:
n =2 m=1 P=0,5
Решение:
n =2 m=1 P=0,5
Слайд 6 Правило.
Если при одном подбрасывании монеты всего равновозможных результатов 2, то
для двух – 2•2
для трех – 2•2•2
для n бросаний-2•2•2…….•2 =2ⁿ
Задачу можно сформулировать по-другому: бросили 5 монет одновременно. На решение это не повлияет!
для трех – 2•2•2
для n бросаний-2•2•2…….•2 =2ⁿ
Задачу можно сформулировать по-другому: бросили 5 монет одновременно. На решение это не повлияет!
Слайд 7
Задача №2.
В случайном эксперименте бросают две игральные кости.
Найдите вероятность того, что в сумме
выпадет более 10 очков. Результат округлите
до сотых.
выпадет более 10 очков. Результат округлите
до сотых.
Слайд 8Решение задачи № 2
Результат каждого бросания –
36 равновозможных исходов
Благоприятных исходов
3
Вероятность заданного события
Р = т/п
Р = 3/36 = 0,083… = 0,08
Вероятность заданного события
Р = т/п
Р = 3/36 = 0,083… = 0,08
Слайд 9II.Задачи, где все элементарные события выписывать сложно,но можно подсчитать их количество.
На
соревнования по метанию ядра приехали 2 спортсмена из Великобритании, 2 из Испании и 4 из Швейцарии. Порядок выступлений определяется жребием. Найдите вероятность того, что восьмым будет выступать спортсмен из Испании.
Слайд 10Решение задачи № 3
Обратить внимание!
(первым, вторым, седьмым –не важно!)
n=2+2+4=8
m=2 (благоприятные
исходы-испанцы 2 человека)
Р = 2/8=0,25
Р = 2/8=0,25
Слайд 11III.Использование формулы вероятности противоположного события.
Р(А‾) +Р(А) =1
В среднем из 500 фонариков,
поступивших в продажу, 5 неисправны. Найдите вероятность того, что один купленный фонарик окажется исправным.
Слайд 12Решение задачи №4:
На стенде испытаний – 500 фонариков
Неисправных среди них 5
Вероятность
купить неисправный фонарик 5 : 500 = 0,01
Значит, исправный можно купить с вероятностью 1- 0,01 = 0,99
Значит, исправный можно купить с вероятностью 1- 0,01 = 0,99
Слайд 13Задача №4.2
Вероятность того, что новая шариковая ручка пишет плохо равна 0,05.Покупатель
в магазине выбирает одну новую ручку.
Найти вероятность того, что эта ручка пишет хорошо.
Найти вероятность того, что эта ручка пишет хорошо.
Слайд 14Решение задачи №4.2
1.Определим событие А – выбранная ручка пишет хорошо.
2.Противоположное событие
А‾
3.Вероятность противоположного события
Р(А‾)=0,05
Применяя формулу вероятности противоположных событий, получаем ответ:
Р(А)=1-Р( А‾)=1-0,05=0,95
3.Вероятность противоположного события
Р(А‾)=0,05
Применяя формулу вероятности противоположных событий, получаем ответ:
Р(А)=1-Р( А‾)=1-0,05=0,95
Слайд 15IV. Задачи, где искомые значения не выводятся из текста.
Обратить внимание!
n!=1•2•3•4
• … •n
0!=1
Cn ª=n!/а!(n-а)!
0!=1
Cn ª=n!/а!(n-а)!
Слайд 16Задача №5
В группе из 20 студентов надо выбрать 2 представителей для
выступления на конференции. Сколькими способами можно это сделать?
Слайд 18Литература:
«Вероятность и статистика. 5-9 классы.» Е.А. Бунимович, В.А.Булычёв. Издательство «Дрофа»,2006.
Бунимович Е.А.
Вероятностно-статистическая линия в базовом школьном курсе математики.- Математика в школе, №4, 2002.
«ЕГЭ. 3000 задач с ответами. Математика с теорией вероятностей и статистикой» под редакцией А.Л. Семёнова, И.В. Ященко. Разработано МИОО. 2011г.
«ЕГЭ. 3000 задач с ответами. Математика с теорией вероятностей и статистикой» под редакцией А.Л. Семёнова, И.В. Ященко. Разработано МИОО. 2011г.
Слайд 19Сайты:
Материалы с сайта www.1september.ru,
фестиваль педагогических идей «Открытый урок»
Материалы с
сайта www.mathege.ru