- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация по математику на тему Тройной интеграл (студентов ВУЗа)
Содержание
- 1. Презинтация по математику на тему Тройной интеграл (студентов ВУЗа)
- 2. ПЛАН:Задача, приводящая к понятию тройного интегралаОпределение
- 3. 1. Задача, приводящая к понятию тройного интеграла
- 4. 2. Определение и свойства тройного интеграла Пусть
- 5. Пусть di – диаметр (ΔVi) ,
- 6. ТЕОРЕМА 1 (необходимое условие существования тройного интеграла).
- 7. Правильная трехмерная область Пусть пространственная область
- 8. 3. СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА 2. Постоянный множитель
- 9. 4. Если область интегрирования (V) разбита на две
- 10. Слайд 10
- 11. 4. Вычисление тройного интеграла Назовем область (V)
- 12. ТЕОРЕМА 3. Пусть функция f(x,y,z) интегрируема в
- 13. Вычисление тройного интеграла Если область имеет
- 14. Вычисление тройного интеграла Пример 1. Вычислить
- 15. Решение.
- 16. Слайд 16
- 17. 5. Замена переменных в тройном интеграле Пусть
- 18. Пусть отображение (1) удовлетворяет следующим условиям: а) отображение
- 19. Два наиболее часто встречающихся случая замены переменных
- 20. 1) x = ρ·cosφ·sinθ , y =
- 21. 6. Геометрические и физические приложения тройных
- 22. Объем тела Общая формула для вычисления объема (независимо от системы координат) имеет вид:
- 23. Объем тела Объём пространственной области V в цилиндрических координатах:
- 24. 3) Статические моменты тела (V) относительно плоскостей xOy, yOz и xOz равны соответственно:
- 25. 5) Моменты инерции тела (V) относительно осей Ox, Oy и Oz равны соответственно:
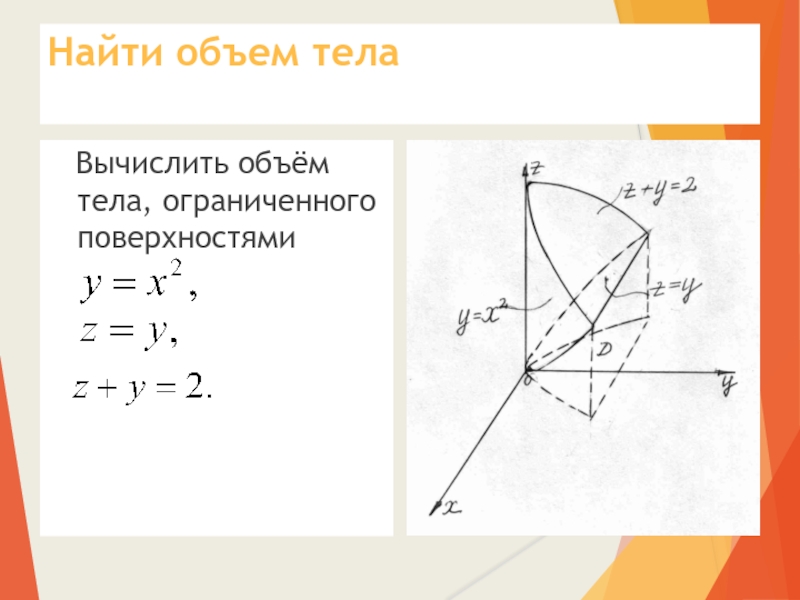
- 26. Найти объем тела Вычислить объём тела, ограниченного поверхностями
- 27. РешениеНайдём линию пересечения плоскостей, ограничивающих тело сверху и снизу. Очевидно, это y=1.
- 28. Слайд 28
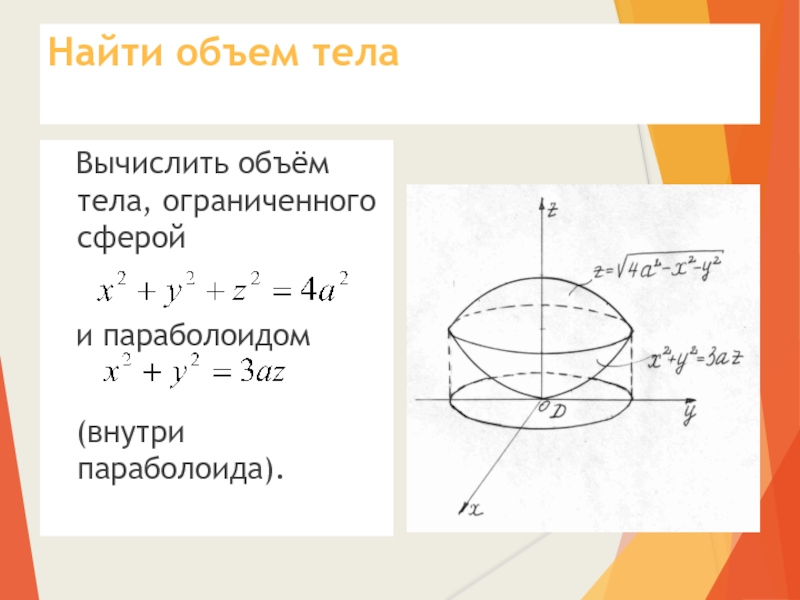
- 29. Найти объем тела Вычислить объём тела, ограниченного сферой и параболоидом (внутри параболоида).
- 30. Слайд 30
- 31. Подставляя z= в одно из уравнений системы, получим
- 32. Слайд 32
- 33. Список использованной литературы:1. Г. М. Фихтенгольц. Математический
Слайд 2 ПЛАН:
Задача, приводящая к понятию тройного интеграла
Определение и свойства тройного интеграла
Свойства
Вычисление тройного интеграла
Замена переменных в тройном интеграле
Геометрические и физические приложения тройных интегралов
Слайд 31. Задача, приводящая к понятию тройного интеграла
Пусть (V) – замкнутая
γ = γ(x,y,z) – плотность распределения массы в области (V)
ЗАДАЧА. Найти массу m тела (V).
1. Разобьем (V) на n частей (ΔV1), (ΔV2), … , (ΔVn).
2. Если (ΔVi) – мала, то (ΔVi) можно считать однородной и ее масса mi ≈ γ(Pi) · ΔVi,
где ΔVi – объем (ΔVi), Pi – произвольная точка из (ΔVi) .
Тогда
Слайд 42. Определение и свойства тройного интеграла
Пусть (V) – кубируемая (т.е.
1. Разобьем область (V) произвольным образом на n частей, не имеющих общих внутренних точек:
(ΔV1), (ΔV2), … , (ΔVn).
2. В каждой области (ΔVi) выберем произвольную точку Pi(ξi;ηiζi) и вычислим произведение f(Pi) · ΔVi, где ΔVi – площадь области (ΔVi).
Сумму
назовем интегральной суммой для функции f(x,y,z) по области (V) (соответствующей данному разбиению области (V) и данному выбору точек Pi).
Слайд 6ТЕОРЕМА 1 (необходимое условие существования тройного интеграла). Если функция f(x,y,z) интегрируема
ТЕОРЕМА 2 (достаточные условия существования тройного интеграла). Если
1) область (V) – кубируемая,
2) функция f(x,y,z) ограничена в области (V) и непрерывна всюду за исключением некоторого множества точек объема нуль,
то f(x,y,z) интегрируема в области (V) .
Слайд 7Правильная трехмерная область
Пусть пространственная область V, ограниченная замкнутой поверхностью
1) всякая прямая, параллельная оси Oz, проведённая через внутреннюю точку области V, пересекает поверхность G в двух точках;
2) вся область V проектируется на плоскость Oxy в правильную область D.
Тогда область V мы будем называть правильной трёхмерной областью.
Слайд 83. СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА
2. Постоянный множитель можно выносить за знак
3. Тройной интеграл от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме тройных интегралов от этих функций, т.е.
Слайд 94. Если область интегрирования (V) разбита на две части (V1) и (V2),
(свойство аддитивности тройного интеграла).
Слайд 114. Вычисление тройного интеграла
Назовем область (V) правильной в направлении оси
Слайд 12ТЕОРЕМА 3. Пусть функция f(x,y,z) интегрируема в области (V).
Если область
где z=f1(x,y) , z=f2(x,y) – уравнения нижней и верхней границ области (V) соответственно, (σ) – проекция области (V) на плоскость xOy.
Интеграл
называют повторным и записывают в виде
Интеграл
называют внутренним .
Слайд 13Вычисление тройного интеграла
Если область имеет вид как на рисунке,
=
Слайд 14Вычисление тройного интеграла
Пример 1. Вычислить
где V
x=0, y=0, z=0.
Слайд 175. Замена переменных в тройном интеграле
Пусть (V) – замкнутая кубируемая
f(x,y,z) – непрерывна в области (V) всюду, кроме, может быть, некоторого множества точек, объема нуль.
Тогда существует интеграл
Введем новые переменные по формулам:
x = φ(u,v,w), y = ψ(u,v,w), z = χ(u,v,w), (u,v,w)∈(G) (1)
ГЕОМЕТРИЧЕСКАЯ интерпретация (1): отображение области (G) пространства Cuvw на некоторую область пространства Oxyz .
Пусть функции φ(u,v,w), ψ(u,v,w), χ(u,v,w) такие, что (1) является отображением области (G) на область (V)
(т.е. если точка (u,v,w) пробегает область (G) , то соответствующая ей точка (x,y,z) пробегает область (V) ) .
Слайд 18Пусть отображение (1) удовлетворяет следующим условиям:
а) отображение (1) взаимно однозначно в
б) функции φ(u,v,w), ψ(u,v,w), χ(u,v,w) имеют в области (G) непрерывные частные производные первого порядка;
Формулу (2) называют формулой замены переменных в тройном интеграле, определитель I(u,v,w) называют якобианом отображения (1).
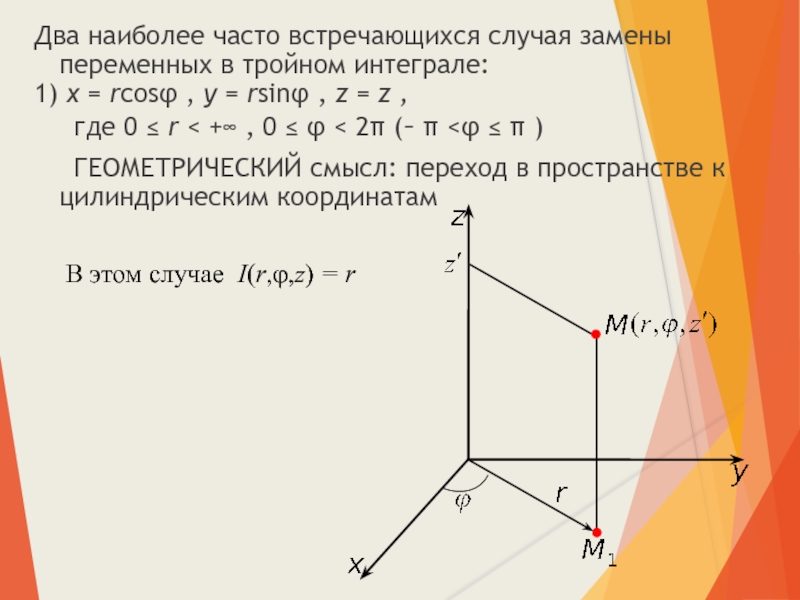
Слайд 19Два наиболее часто встречающихся случая замены переменных в тройном интеграле:
1) x
где 0 ≤ r < +∞ , 0 ≤ φ < 2π (– π <φ ≤ π )
ГЕОМЕТРИЧЕСКИЙ смысл: переход в пространстве к цилиндрическим координатам
В этом случае I(r,φ,z) = r
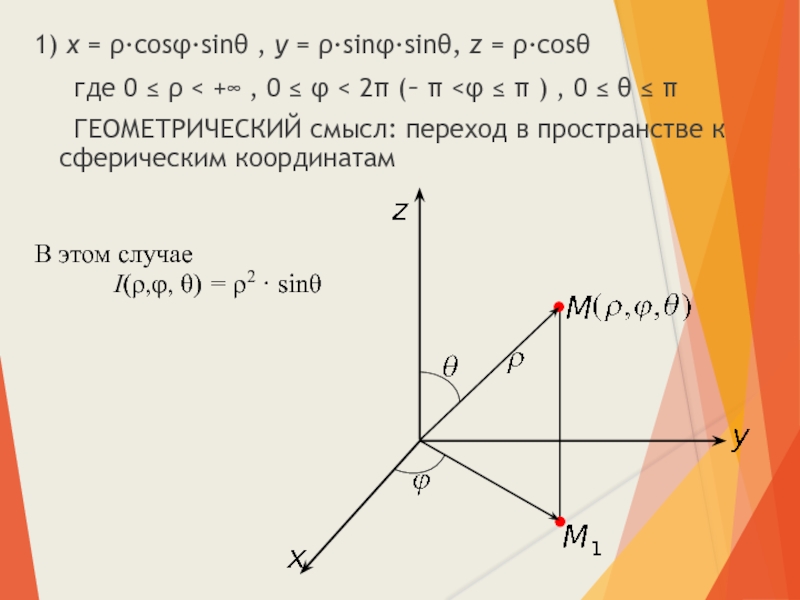
Слайд 201) x = ρ·cosφ·sinθ , y = ρ·sinφ·sinθ, z = ρ·cosθ
где 0 ≤ ρ < +∞ , 0 ≤ φ < 2π (– π <φ ≤ π ) , 0 ≤ θ ≤ π
ГЕОМЕТРИЧЕСКИЙ смысл: переход в пространстве к сферическим координатам
В этом случае
I(ρ,φ, θ) = ρ2 · sinθ
Слайд 216. Геометрические и физические приложения
тройных интегралов
Пусть (V) – материальное
Тогда
1) Объем V кубируемого тела (V)∊ Oxyz:
Слайд 243) Статические моменты тела (V) относительно плоскостей xOy, yOz и xOz равны
Слайд 27Решение
Найдём линию пересечения плоскостей, ограничивающих тело сверху и снизу. Очевидно, это
Слайд 29Найти объем тела
Вычислить объём тела, ограниченного сферой
(внутри параболоида).
Слайд 33Список использованной литературы:
1. Г. М. Фихтенгольц. Математический анализ. 3 том. 308
2. В. А. Зорич. Москва. 2002 г. Математический анализ.
3. К.Н.Лунгу. Д.Т.Письменный. С.Н.Федин. Ю.А.Шевченко. Москва. 2008 г. Сборник задач по высшей математике.
4. Г.Н.Берман. Москва. Сборник задач по курсу математического анализа.
5. П.П.Коровкин. Москва. Математический анализ.