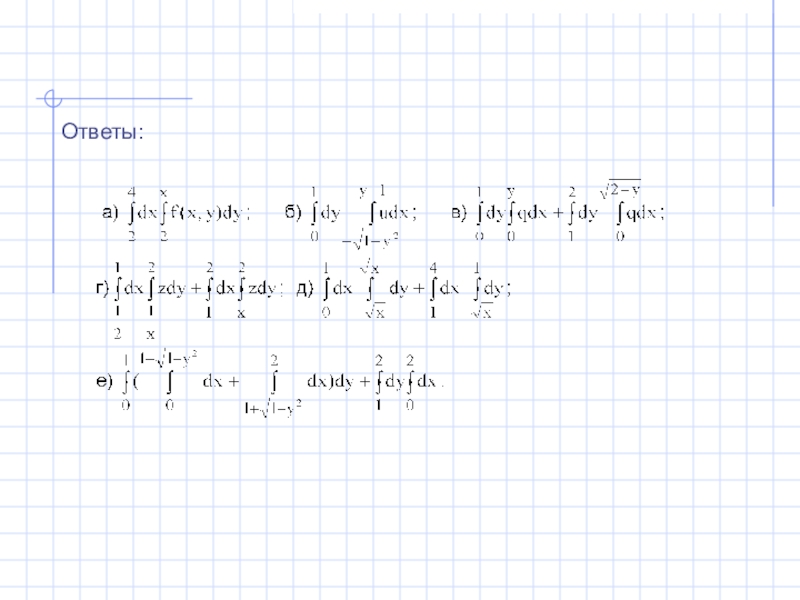- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация по математику на тему Двойной интеграл (студентов ВУЗа)
Содержание
- 1. Презинтация по математику на тему Двойной интеграл (студентов ВУЗа)
- 2. Двойной интегралДИ в декартовых координатахЗамена переменных в
- 3. ДИ в декартовых координатахРассмотрим область σ⊆R2 и
- 4. ДИ в декартовых координатахОбласть σ⊆R2 называется горизонтально-правильной,
- 5. Замена переменных в двойном интегралеЗаменим переменные x
- 6. Замена переменных в двойном интегралеВычислить двойной интеграл
- 7. Найдем уравнения линий, ограничивающих область D*Замена переменных в двойном интеграле4/13
- 8. Выразим переменные x и y через u
- 9. Найдем якобиан преобразования: Замена переменных в двойном интеграле6/13
- 10. D*Построим область D*.Расставим пределы интегрирования, пользуясь формулой (1):Вычислим двукратный интеграл:Замена переменных в двойном интеграле7/13
- 11. Двойной интеграл в полярных координатахРассмотрим частный случай
- 12. Формула замены переменных принимает вид: Двойной интеграл
- 13. Расставим пределы интегрирования: Внутренний интеграл здесь берется при постоянном φ. Двойной интеграл в полярных координатахD*10/13
- 14. Замечания12Переход к полярным координатам целесообразен, когда подынтегральная
- 15. Вычислить Перейдем к полярным координатам:Двойной интеграл в полярных координатахИзобразим область D в декартовой системе координат.3D12/13
- 16. 3DВ полярной системе координат эта область будет определяться неравенствами: r = 3Двойной интеграл в полярных координатах3002π13/13
- 17. Отработка отдельных блоков схемы вычисления ДИПример
- 18. Пример № 2.Вычислить повторный интеграл Решение1. Вычислим
- 19. Задания по теме1. Вычислить двукратные (повторные) интегралы:Ответы:
- 20. Ответы:
- 21. 3. Вычислить двойной интеграл
Слайд 2Двойной интеграл
ДИ в декартовых координатах
Замена переменных в ДИ
ДИ в полярных координатах
Отработка
Задания по теме
1/13
Слайд 3ДИ в декартовых координатах
Рассмотрим область σ⊆R2 и проведем вертикальные прямые х=с
Вертикально-правильную область σ можно задать системой неравенств
σ: (1)
где [a,b] — проекция области σ на ось ОХ. Двойной интеграл по вертикально-правильной области σ, заданной системой неравенств (1), вычисляется с помощью повторного интеграла:
Слайд 4ДИ в декартовых координатах
Область σ⊆R2 называется горизонтально-правильной, если каждая горизонтальная прямая
[c; d] - проекция σ на ОУ.
Область σ можно задать системой неравенств
σ: (2)
Двойной интеграл по горизонтально-правильной области σ, заданной системой неравенств (2), вычисляется с помощью повторного интеграла
Слайд 5Замена переменных в двойном интеграле
Заменим переменные x и y :
Если функции
а функция f(x, y) непрерывна в области D, то справедлива формула замены переменной в двойном интеграле:
определитель Якоби (якобиан)
Пусть в замкнутой области D плоскости XOY задана непрерывная функция z = f(x, y).
2/13
Слайд 6
Замена переменных в двойном интеграле
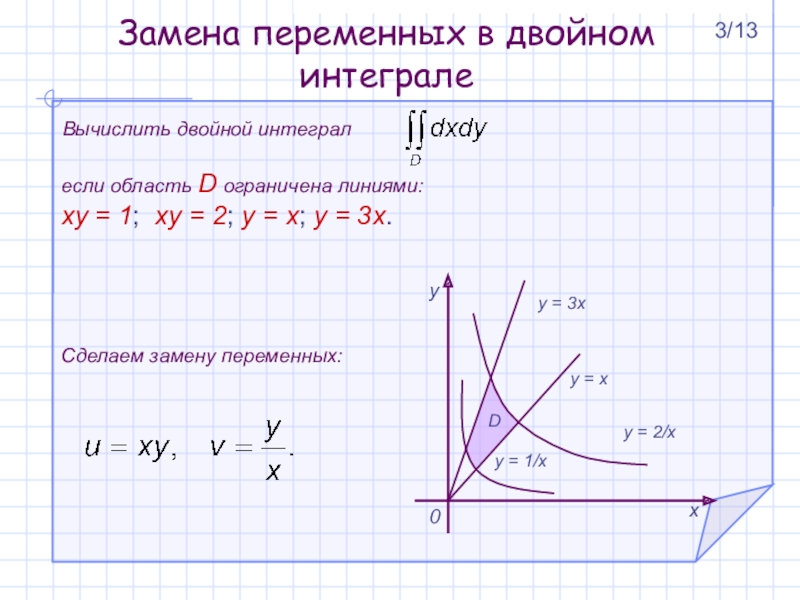
Вычислить двойной интеграл
если область D ограничена
xy = 1; xy = 2; y = x; y = 3x.
D
Сделаем замену переменных:
3/13
Слайд 8
Выразим переменные x и y через u и v.
Найдем частные
Замена переменных в двойном интеграле
5/13
Слайд 10
D*
Построим область D*.
Расставим пределы интегрирования, пользуясь формулой (1):
Вычислим двукратный интеграл:
Замена переменных
7/13
Слайд 11Двойной интеграл в полярных координатах
Рассмотрим частный случай замены переменных: замену декартовых
В качестве u и v возьмем полярные координаты r и φ. Они связаны с декартовыми координатами формулами:
Правые части в этих равенствах – непрерывно дифференцируемые функции.
Якобиан преобразования равен:
8/13
Слайд 12
Формула замены переменных принимает вид:
Двойной интеграл в полярных координатах
Область в
Пусть область D* задана линиями в полярной системе координат:
Лучами
D*
Кривыми
Такая область называется правильной областью в полярной системе координат:
луч, выходящий из полюса, пересекает границу области не более, чем в двух точках.
9/13
Слайд 13
Расставим пределы интегрирования:
Внутренний интеграл здесь берется при постоянном φ.
Двойной
D*
10/13
Слайд 14Замечания
1
2
Переход к полярным координатам целесообразен, когда подынтегральная функция имеет вид f(x2+y2)
На практике переход к полярным координатам осуществляется путем замены
Двойной интеграл в полярных координатах
Уравнения линий, ограничивающих область D, также преобразуются к полярным координатам.
Преобразование области D в область D* не выполняют, а совмещают декартовы и полярную системы координат, находят нужные пределы интегрирования по r и φ.
3
11/13
Слайд 15
Вычислить
Перейдем к полярным координатам:
Двойной интеграл в полярных координатах
Изобразим область D
3
D
12/13
Слайд 16
3
D
В полярной системе координат эта область будет определяться неравенствами:
r =
Двойной интеграл в полярных координатах
3
0
0
2π
13/13
Слайд 17Отработка отдельных блоков схемы
вычисления ДИ
Пример № 1. Вычислить повторный интеграл
Решение
Вычислим внутренний интеграл, рассматривая в нем переменную х как параметр (т.е. const):
2. Вычислим внешний интеграл
Слайд 18Пример № 2.
Вычислить повторный интеграл
Решение
1. Вычислим внутренний интеграл, рассматривая в
2. Вычислим внешний интеграл
Вычисление можно записывать короче:
Слайд 19Задания по теме
1. Вычислить двукратные (повторные) интегралы:
Ответы: 26; -11,2;
2. Изменить порядок интегрирования в следующих интегралах:
Слайд 21
3. Вычислить двойной интеграл
Ответ: 9.
4. Вычислить двойной интеграл , если область D задана неравенствами ; у≥х; 0≤х≤2.
Ответ: .
5. Вычислить двойные интегралы по областям, ограниченным указанными линиями
a) ; y=0; y= ; б) ; y=0; y=x; x+y=π/2;
в) ; x=y2; y=x2.
Ответы: a5 ; 1/2; -1/504.