Удивительный символ математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Удивительный символ математики
Содержание
- 1. Презентация Удивительный символ математики
- 2. Актуальность выбранной темыВ нашей жизни мы часто
- 3. ГИПОТЕЗА:Мы предположили, что математическая фигура обозначающий бесконечность должен обладать какими- то особыми уникальными свойствами.
- 4. ЦЕЛЬ И ЗАДАЧИЦЕЛЬИзучить свойства математической фигуры обозначающей
- 5. ВведениеМатематики сравнивают знак
- 6. Август Фердинанд Мёбиус (17.11.1790-1868) немецкий геометр, ученик
- 7. Версии поразительного открытия МёбиусаА случилось это в
- 8. Свойства Ленты МёбиусаОдносторонность - топологическое свойство ленты Мёбиуса,
- 9. Ориентированность ленты МёбиусаЛента Мёбиуса является простейшей односторонней поверхностью,
- 10. Изготовление и знакомство с лентой Мёбиуса
- 11. Проведение опытов с листом Мёбиуса.На одной из
- 12. Опыт 2 доказывающий односторонность Ленты Мёбиуса
- 13. Опыт 3 доказывающий, что у ленты
- 14. Опыт 4 доказывающий связанность ленты Мёбиуса.Разрезаем ленту
- 15. Опыт 5, доказывающий связанность ленты Мёбиуса.Разрежем кольцо
- 16. Выводы Лента Мёбиуса имеет одну сторону (поверхность).
- 17. Лента Мёбиуса вокруг нас
- 18. Слайд 18
- 19. ВЫВОДЫ Таким образом, наша гипотеза подтвердилась. Мы
- 20. Лист Мебиуса – символ математики, Что служит
- 21. Использованные источники:https://kalkpro.ru/interesting-facts/lenta-mebiusa/ https://wond-world.livejournal.com/2130848.html https://www.kakprosto.ru/kak-250962-gde-ispolzuetsya-lenta-mebiusa#ixzz5XhYLKZZP https://kozelrozel.jimdo.com/ https://kozelrozel.jimdo.com/головоломки/лист-мебиуса/лист-мёбиуса-в-архитектуре-и-искусстве/
- 22. Спасибо за внимание!
Слайд 1Работу выполнили : ученики 5 «В» класса
Темнова Анна и Лаптев Иван
Руководитель:
Слайд 2Актуальность выбранной темы
В нашей жизни мы часто слышим фразы о бесконечности:
в математике говорят, что ряд натуральных чисел бесконечен;
на обществознании утверждают, что человеческая глупость бесконечна;
на географии - слышим о бесконечной вселенной и.т.д.
Практически все знают, как выглядит символ бесконечности, напоминающий перевернутую восьмерку. Этот знак называют еще «лемниската», что с древнегреческого означает лента. Представьте себе, что символ бесконечности очень похож на реально существующую математическую фигуру. Вот нас и заинтересовало- какие свойства имеет эта фигура.
Слайд 3ГИПОТЕЗА:
Мы предположили, что математическая фигура обозначающий бесконечность должен обладать какими- то
Слайд 4ЦЕЛЬ И ЗАДАЧИ
ЦЕЛЬ
Изучить свойства математической фигуры обозначающей бесконечность и опытно-экспериментальным путём
ЗАДАЧИ
Познакомиться с историей появления символа.
Познакомиться с биографией автора и с историей его замечательного открытия.
Описать процесс изготовления символа бесконечности.
Изучить и исследовать опытным путем его свойства.
Найти этот символ в нашем окружении
Сделать выводы
Составить презентацию
Слайд 5 Введение
Математики сравнивают знак бесконечности с лентой Мебиуса.
Многие философы и астрономы, историки и психологи – все они применяют в своих гипотезах символ бесконечности, которую называют лентой Мебиуса. Так, Альберт Эйнштейн считал, что вселенная замкнута в виде кольца, подобно ленте Мебиуса, а философами строятся целые теории, основанные на удивительных свойствах этого математического объекта.
Нам захотелось как можно больше узнать о ленте Мебиуса еще и потому, что эту ленту часто называют загадочной.
Слайд 6Август Фердинанд Мёбиус
(17.11.1790-1868)
немецкий геометр, ученик великого Гаусса - «короля
Мёбиус был первоначально астрономом, так как в те времена изучение математики не встречало поддержки, а занятие астрономией приветствовалось. Однако занимаясь астрономией, Мёбиус много размышлял о математике.
Историческая справка
Слайд 7Версии поразительного открытия Мёбиуса
А случилось это в 1865 году.
когда наблюдал
когда портной неправильно вшил манжет рубашки.
разглядывая ленту, концы которой однажды неправильно сшила его служанка Марта. Он с восхищением воскликнул: «Ай да, Марта! Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!»
Слайд 8Свойства Ленты Мёбиуса
Односторонность - топологическое свойство ленты Мёбиуса, характерное только для него.
Непрерывность –
Связность – чтобы разделить квадрат на две части, нам потребуется только один разрез; чтобы разделить надвое кольцо-два разреза. Что касается ленты Мёбиуса, то количество связей меняется в зависимости от смены количества оборотов ленты: если один оборот – двусвязен и т.д.
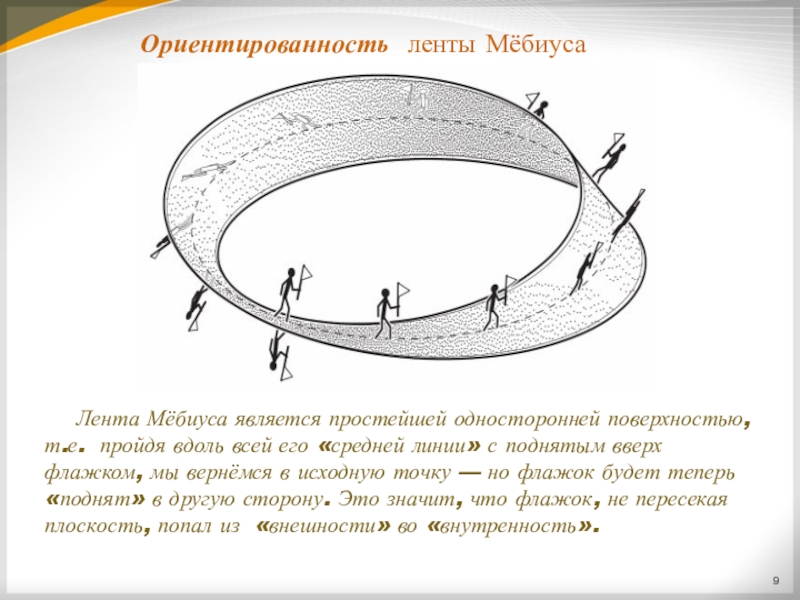
Ориентированность – свойство, отсутствующее у листа Мёбиуса. Так, если бы человек смог пропутешествовать по всем по всем изгибам лента Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение.
Слайд 9Ориентированность ленты Мёбиуса
Лента Мёбиуса является простейшей односторонней поверхностью, т.е. пройдя вдоль всей
Слайд 11Проведение опытов с листом Мёбиуса.
На одной из сторон каждого кольца ставим
Опыт 1
доказывающий односторонность Ленты Мёбиуса
Вывод: Поверхность листа Мёбиуса является непрерывной.
Слайд 12Опыт 2
доказывающий односторонность Ленты Мёбиуса
Закрашиваем полностью только одну сторону колец.
Вывод: Поверхность
Слайд 13Опыт 3
доказывающий, что у ленты Мёбиуса один край.
Закрашиваем непрерывной линией
Вывод: У листа Мёбиуса один край.
Слайд 14Опыт 4
доказывающий связанность ленты Мёбиуса.
Разрезаем ленту вдоль по центру.
Вывод :
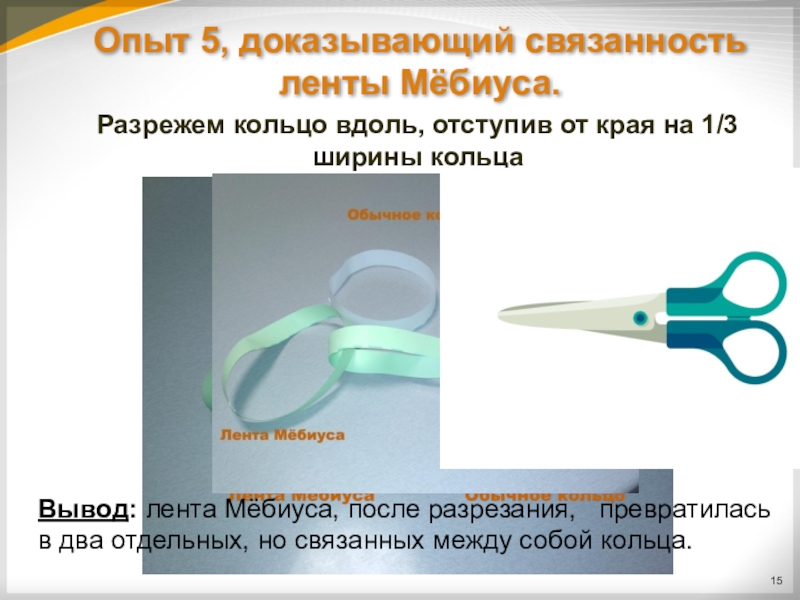
Слайд 15Опыт 5, доказывающий связанность ленты Мёбиуса.
Разрежем кольцо вдоль, отступив от края
Вывод: лента Мёбиуса, после разрезания, превратилась в два отдельных, но связанных между собой кольца.
Слайд 16Выводы
Лента Мёбиуса имеет одну сторону (поверхность). Это подтверждают результаты 1
Лента Мёбиуса имеет один край, согласно результату 3 опыта.
Если пустить по поверхности ленты Мёбиуса движущиеся объекты, они будут двигаться бесконечно долго, т.е. поверхность непрерывна. Это подтверждает 1 опыт .
Ленте Мёбиуса присуще свойство – связность. Что подтверждают опыты 4 и 5.
Слайд 19ВЫВОДЫ
Таким образом, наша гипотеза подтвердилась. Мы смогли самостоятельно создать символ бесконечности
Односторонность (одна сторона и один край)
Непрерывность
Связанность
Зеркальность
А кроме этого мы нашли большое количество предметов окружающих нас и имеющих сходство с этим символом.
Эта работа не исчерпала опыты с лентой Мебиуса. Они бесконечны, интересны и зависят лишь от собственного терпения. Мы обязательно будем возвращаться к опытам с лентой Мебиуса.
Слайд 20Лист Мебиуса – символ математики, Что служит высшей мудрости венцом… Он полон неосознанной
В нем – простота, и вместе с нею – сложность, Что недоступна даже мудрецам: Здесь на глазах преобразилась плоскость В поверхность без начала и конца.
Здесь нет пределов, нет ограничений, Стремись вперед и открывай миры, Почувствуй силу новых ощущений, Прими познанья высшего дары…
Наталья Юрьевна Иванова