- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Сфера и шар
Содержание
- 1. Презентация Сфера и шар
- 2. Слово «сфера» произошло от греческого слова «сфайра»,
- 3. ШАР-символ будущего.
- 4. В Древнем Египте впервые пришли к заключению,
- 5. Человек, держащий шар в руках,символизирует субъекта, несущего
- 6. Таким образом, шар и глобус — это знаки промысла, проведения, вечности, власти и могущество коронованных особ
- 7. Каменное полушарие сферы воплощается в религиозных храмах
- 8. В греко-римской мифологии шар символизировал
- 9. Форма шара в природе ЯгодыПланеты
- 10. Некоторые деревья имеют сферическую форму.
- 11. Определение сферыСферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки
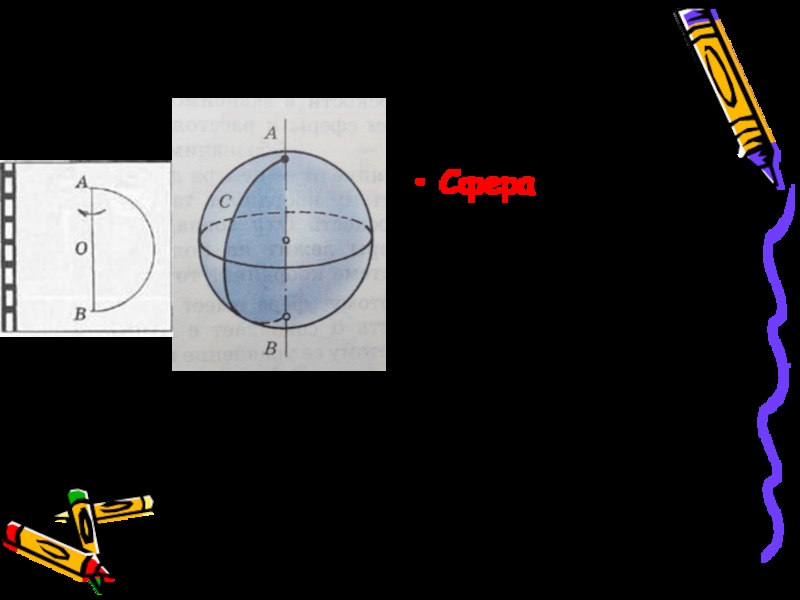
- 12. Сфера –это поверхность, полученная вращением полуокружности вокруг диаметра
- 13. Данная точка (О) называется центром сферы.Любой отрезок,
- 14. Определение шараШар – это тело, которое состоит
- 15. Шаровой сегментШаровым сегментом называется часть шара, отсекаемая от него какой - нибудь плоскостью.
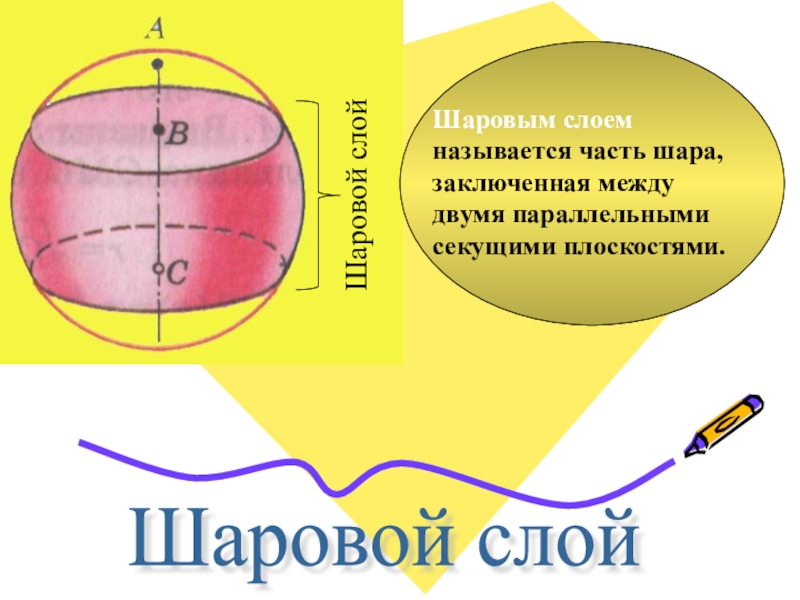
- 16. Шаровой слойШаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.
- 17. Шаровой секторШаровым сектором называется тело, полученное вращением
- 18. Плоскость,проходящая через центр шара,называется диаметральной плоскостью.Сечение шара
- 19. Закрепляем Решите задачу № 573, №574 (а)
- 20. Уравнение сферы в прямоугольной системе координатM(x;y;z)-произвольная точка, принадлежащая сфере./MC/= √(x-x0)2+(y-y0)2+(z-z0)2 т.к. MC=R, то (x-x0)2+(y-y0)2+(z-z0)2=R2
- 21. Задание 1.Найдите координаты центра и радиуса сферы,
- 22. Взаимное расположение сферы и плоскостиОбозначим радиус сферы
- 23. В этой системе координат точка
- 24. Таким образом вопрос о взаимном расположении сферы
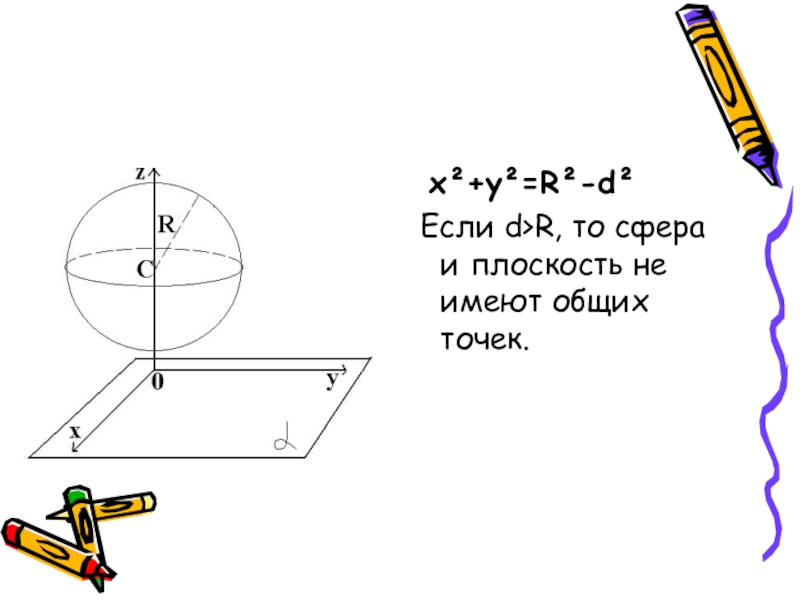
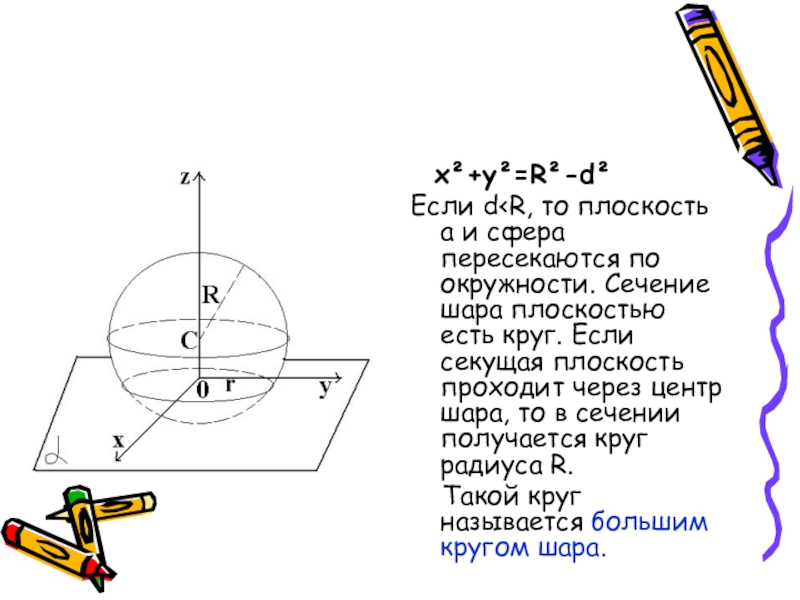
- 25. x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.
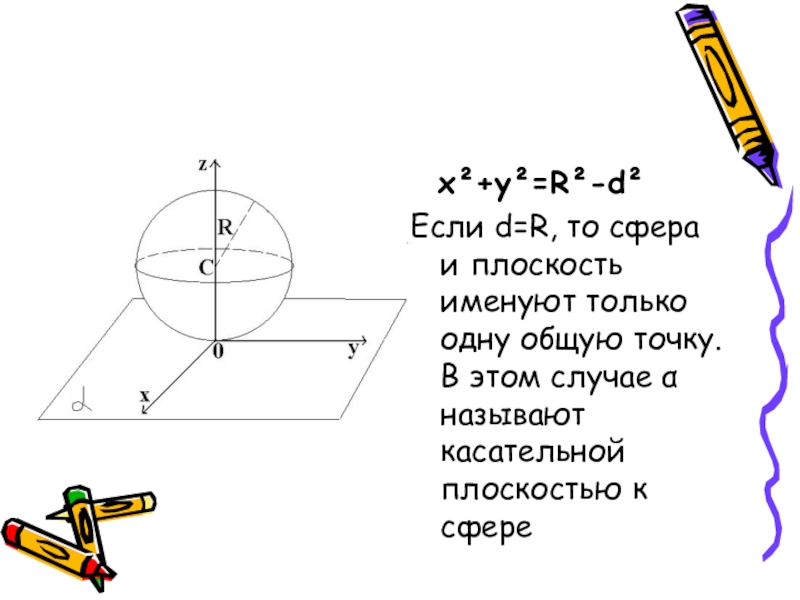
- 26. x²+y²=R²-d²Если d=R, то сфера и
- 27. x²+y²=R²-d²Если d
- 28. Закрепляем Решите задачу №580, №581
- 29. Касательная плоскость к сфереПлоскость, имеющая со сферой
- 30. Теорема: Радиус сферы, проведённый в точку касания
- 31. Обратная теорема: Если радиус сферы перпендикулярен к
- 32. Закрепляем Решите задачу № 592
- 33. Площадь сферыСферу нельзя развернуть на плоскость!Описанным около
- 34. Задание: Площадь сечения сферы, проходящего через её
- 35. Постановка домашнего заданияТеория (п. 64-68) №574 (б,
- 36. Подведение итогов урока.
Слово «сфера» произошло от греческого слова «сфайра», которое переводится на русский язык как «мяч».
Слайд 2Слово «сфера» произошло от греческого слова «сфайра», которое переводится
на русский язык как «мяч».
Слайд 4
В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это
предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.
Слайд 5Человек, держащий шар
в руках,
символизирует субъекта,
несущего тяготы мира
Не случайно подобными
скульптурами украшены некоторые
вокзалы Западной Европы,
например в Хельсинки:
здесь запечатлены тяготы,
выпадающие на плечи
путешественника.
Слайд 6
Таким образом, шар и глобус — это знаки промысла, проведения, вечности,
власти и могущество коронованных особ
Слайд 7Каменное полушарие сферы воплощается в религиозных храмах - куполах православных церквей
в России; ступах, связанных с местом пребывания бодхисаттв в Индии. В Индонезии ступы приобрели форму колокола с каменным шпилем наверху и называются дагобы.
Слайд 8В греко-римской мифологии шар
символизировал удачу, судьбу, ассоциируясь с
Тихэ (Фортуной), стоящей на шаре . Знаменитая картина Пикассо «Девочка на шаре» - танцующая Фортуна.
Слайд 11Определение сферы
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии от данной точки
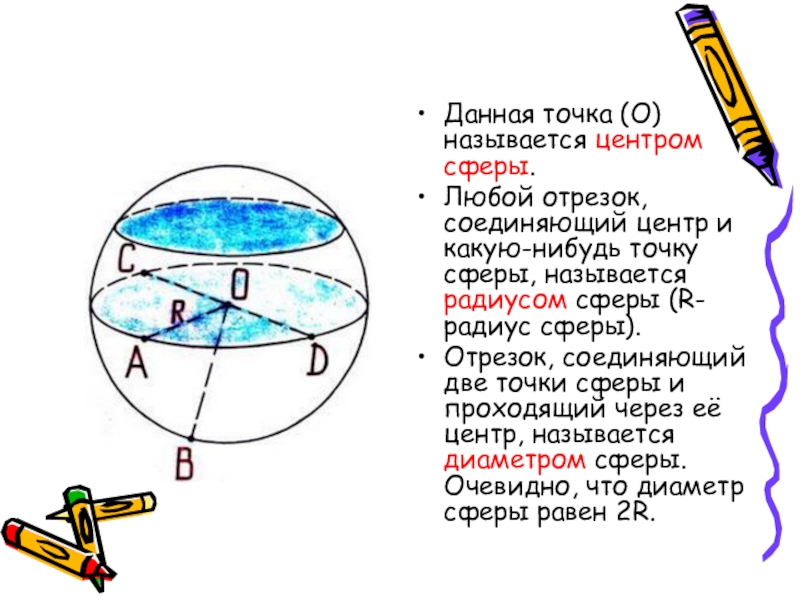
Слайд 13Данная точка (О) называется центром сферы.
Любой отрезок, соединяющий центр и какую-нибудь
точку сферы, называется радиусом сферы (R-радиус сферы).
Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.
Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.
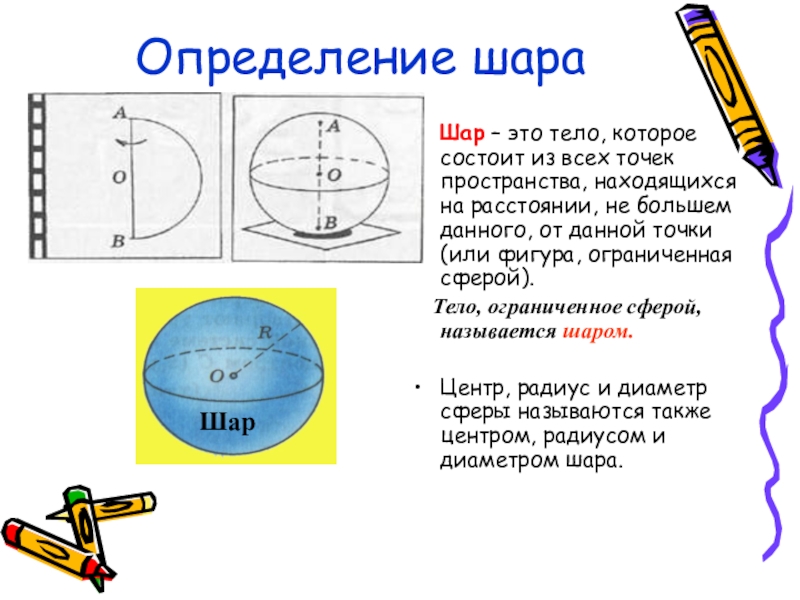
Слайд 14Определение шара
Шар – это тело, которое состоит из всех точек пространства,
находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой).
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
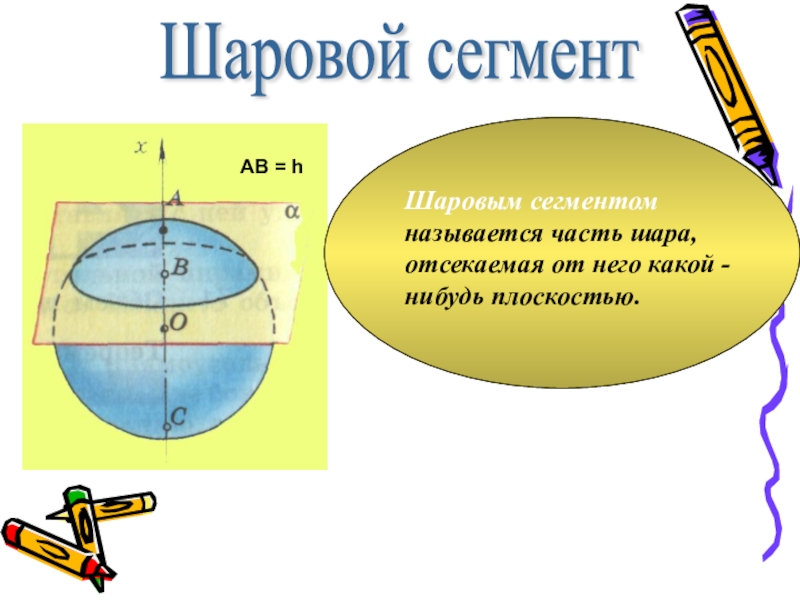
Слайд 15Шаровой сегмент
Шаровым сегментом называется часть шара, отсекаемая от него какой -
нибудь плоскостью.
Слайд 16Шаровой слой
Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими
плоскостями.
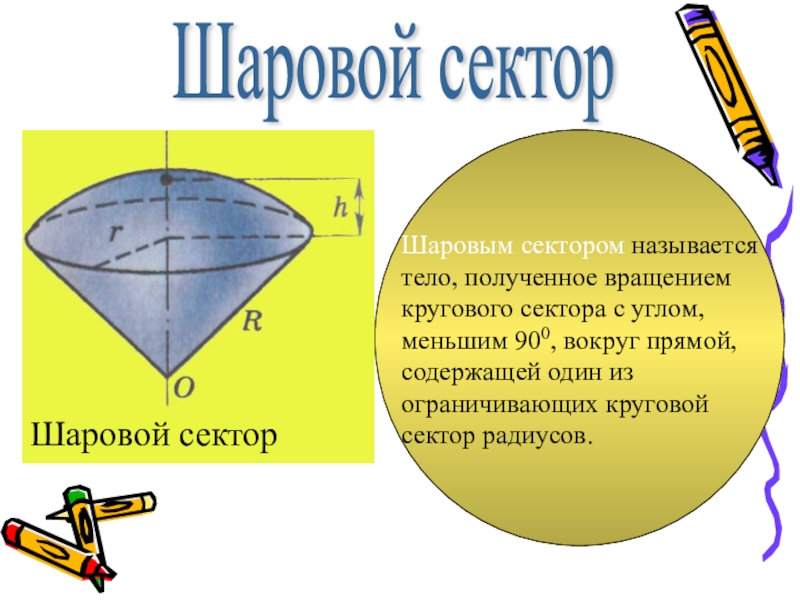
Слайд 17
Шаровой сектор
Шаровым сектором называется тело, полученное вращением кругового сектора с углом,
меньшим 900, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Слайд 18Плоскость,проходящая через центр шара,называется диаметральной плоскостью.
Сечение шара диаметральной плоскостью называется большим
кругом,а сечение сферы - большой окружностью.
Сечение шара
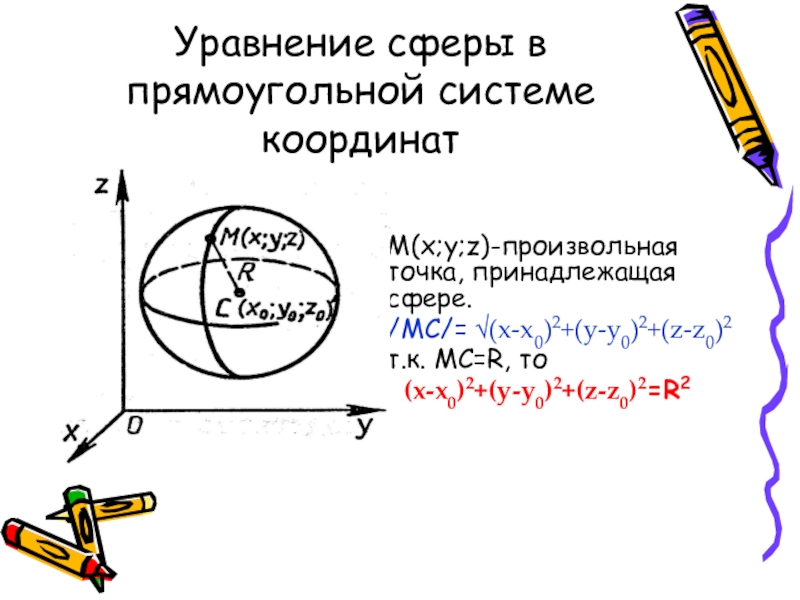
Слайд 20Уравнение сферы в прямоугольной системе координат
M(x;y;z)-произвольная точка, принадлежащая сфере.
/MC/= √(x-x0)2+(y-y0)2+(z-z0)2
т.к.
MC=R, то
(x-x0)2+(y-y0)2+(z-z0)2=R2
(x-x0)2+(y-y0)2+(z-z0)2=R2
Слайд 21Задание
1.Найдите координаты центра и радиуса сферы, заданной уравнением:
x²+y²+z²=49
(X-3)²+(y+2)²+z²=2
2. Напишите уравнение сферы
радиуса R с центром А, если
A(2;-4;7) R=3
A(0;0;0) R=√2
A(2;0;0) R=4
3. Решите задачу №577(а)
A(2;-4;7) R=3
A(0;0;0) R=√2
A(2;0;0) R=4
3. Решите задачу №577(а)
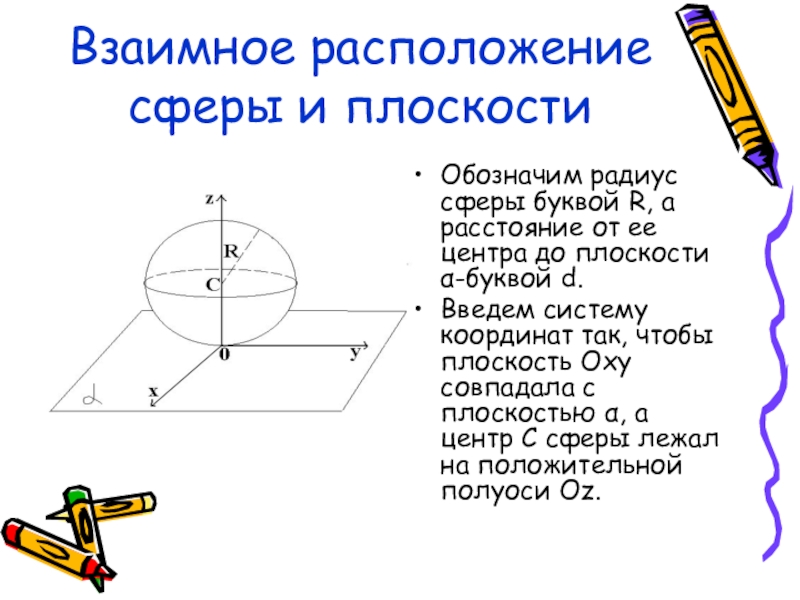
Слайд 22Взаимное расположение сферы и плоскости
Обозначим радиус сферы буквой R, а расстояние
от ее центра до плоскости α-буквой d.
Введем систему координат так, чтобы плоскость Oxy совпадала с плоскостью α, а центр С сферы лежал на положительной полуоси Oz.
Введем систему координат так, чтобы плоскость Oxy совпадала с плоскостью α, а центр С сферы лежал на положительной полуоси Oz.
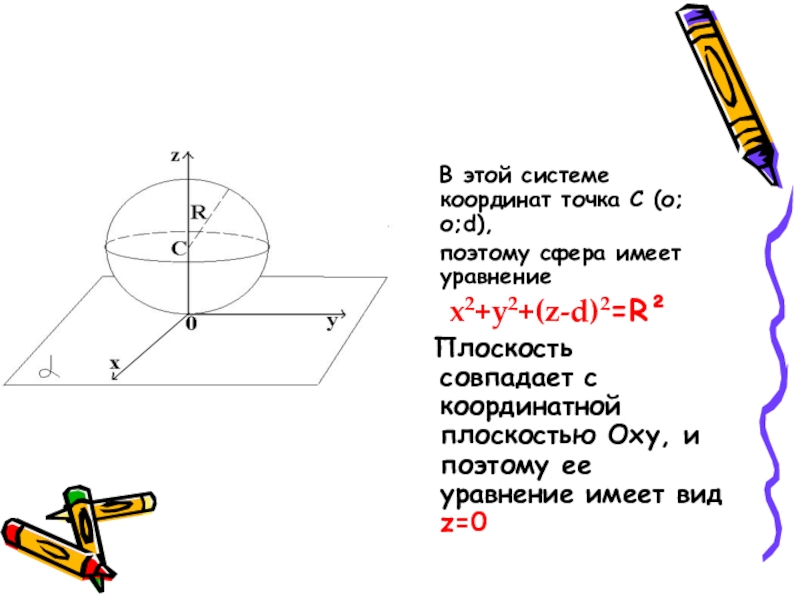
Слайд 23 В этой системе координат точка C (о;о;d),
поэтому сфера имеет уравнение
x2+y2+(z-d)2=R²
Плоскость совпадает с координатной плоскостью Oxy, и поэтому ее уравнение имеет вид z=0
x2+y2+(z-d)2=R²
Плоскость совпадает с координатной плоскостью Oxy, и поэтому ее уравнение имеет вид z=0
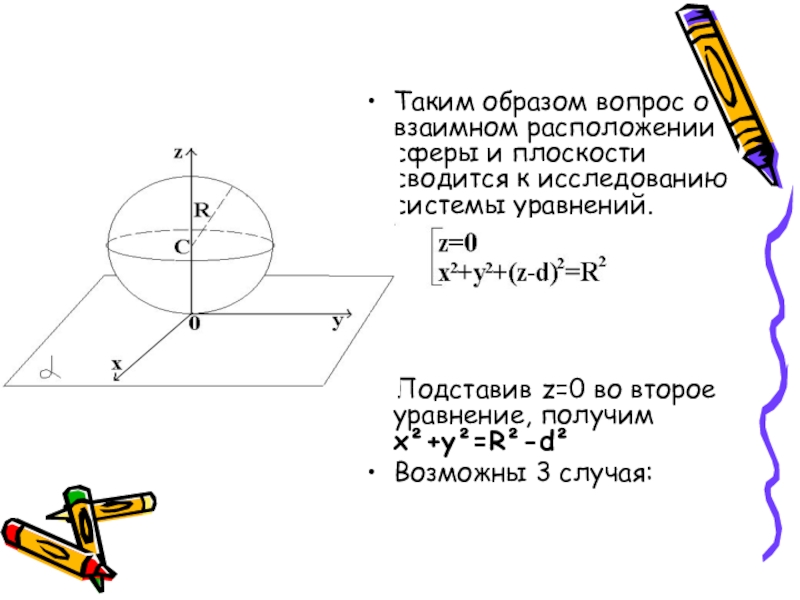
Слайд 24Таким образом вопрос о взаимном расположении сферы и плоскости сводится к
исследованию системы уравнений.
Подставив z=0 во второе уравнение, получим x²+y²=R²-d²
Возможны 3 случая:
Подставив z=0 во второе уравнение, получим x²+y²=R²-d²
Возможны 3 случая:
Слайд 26 x²+y²=R²-d²
Если d=R, то сфера и плоскость именуют только одну
общую точку. В этом случае α называют касательной плоскостью к сфере
Слайд 27 x²+y²=R²-d²
Если d
окружности. Сечение шара плоскостью есть круг. Если секущая плоскость проходит через центр шара, то в сечении получается круг радиуса R.
Такой круг называется большим кругом шара.
Такой круг называется большим кругом шара.
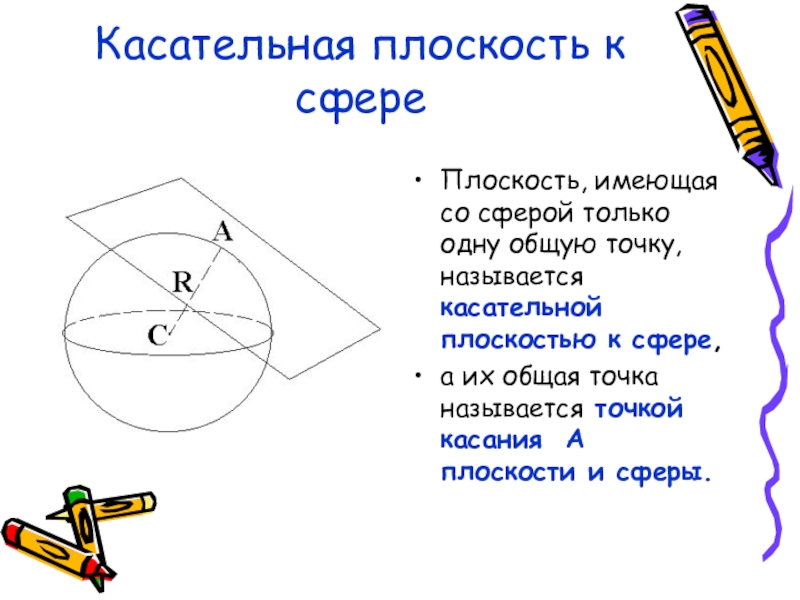
Слайд 29Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую точку,
называется касательной плоскостью к сфере,
а их общая точка называется точкой касания А плоскости и сферы.
а их общая точка называется точкой касания А плоскости и сферы.
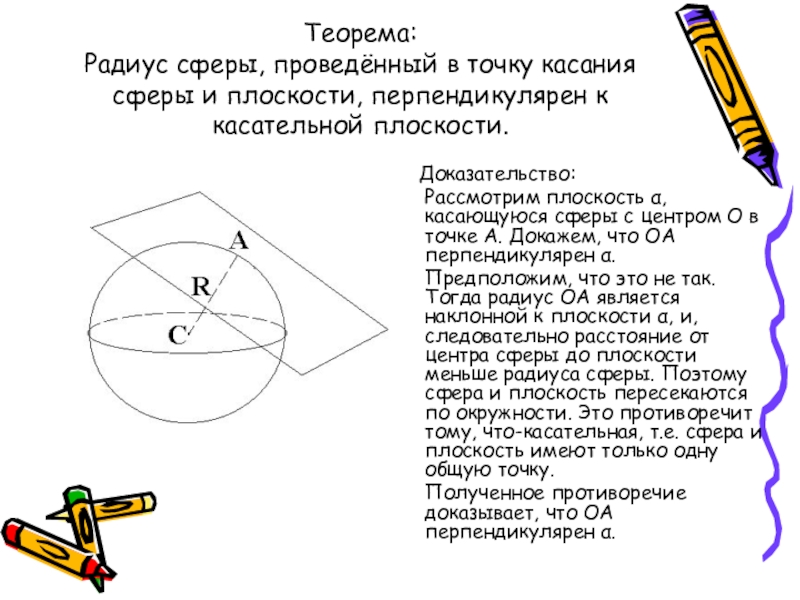
Слайд 30Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к
касательной плоскости.
Доказательство:
Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен α.
Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку.
Полученное противоречие доказывает, что ОА перпендикулярен α.
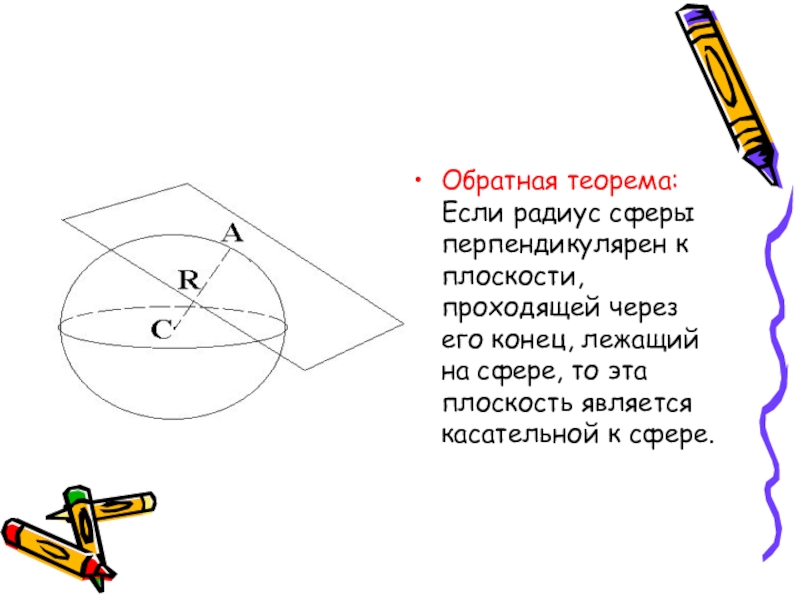
Слайд 31Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец,
лежащий на сфере, то эта плоскость является касательной к сфере.
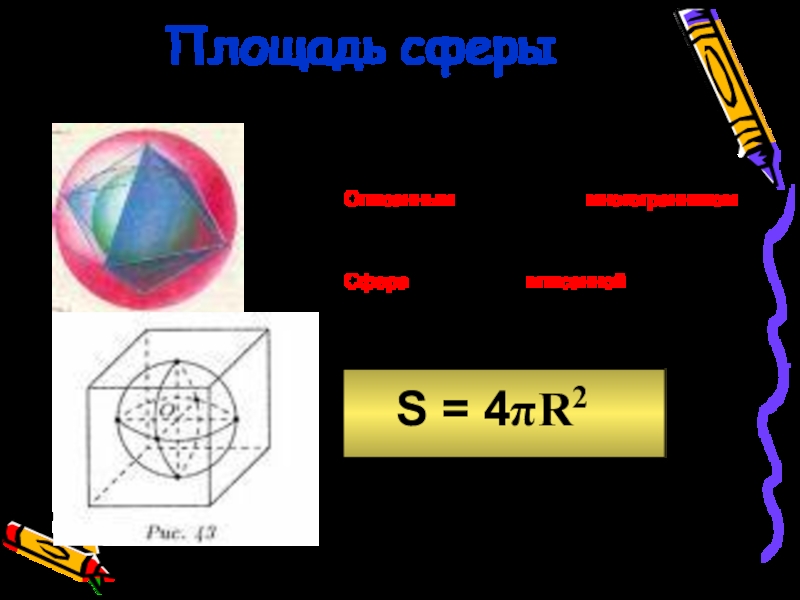
Слайд 33Площадь сферы
Сферу нельзя развернуть на плоскость!
Описанным около сферы многогранником называется многогранник,
всех граней которого которого касается сфера.
Сфера называется вписанной в многогранник
Сфера называется вписанной в многогранник
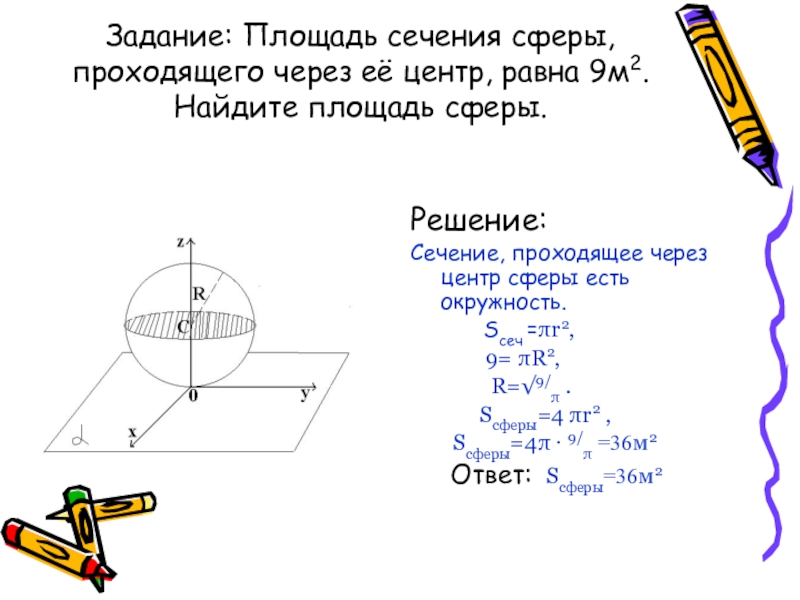
Слайд 34Задание: Площадь сечения сферы, проходящего через её центр, равна 9м2. Найдите
площадь сферы.
Решение:
Сечение, проходящее через центр сферы есть окружность.
Sсеч =πr2,
9= πR2,
R=√9/π .
Sсферы=4 πr2 ,
Sсферы=4π · 9/π =36м2
Ответ: Sсферы=36м2
Слайд 35Постановка домашнего задания
Теория (п. 64-68)
№574 (б, в, г), 577 (б,
в), 587 , 584, 585, 595,597
