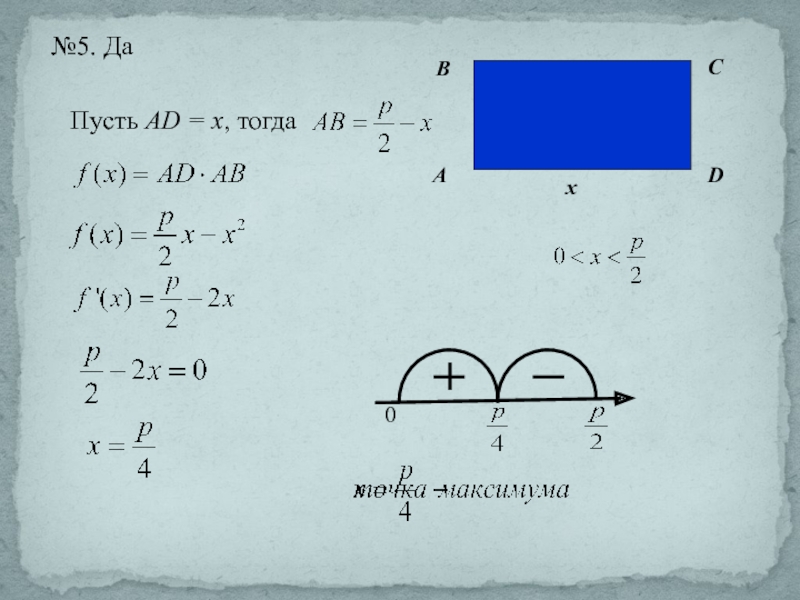Учитель: Житнякова Ольга Сергеевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Производная и ее применение.
Содержание
- 1. Презентация Производная и ее применение.
- 2. Определение производнойОсновные правила дифференцирования и формулы производных
- 3. №1. Найдите производные функций:
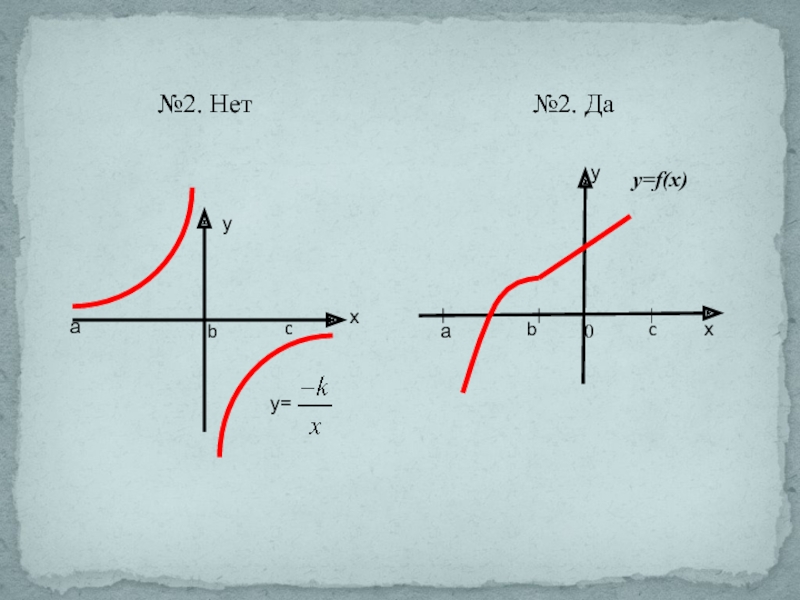
- 4. №2. Из скольких непрерывных «кусков» состоят графики функций:
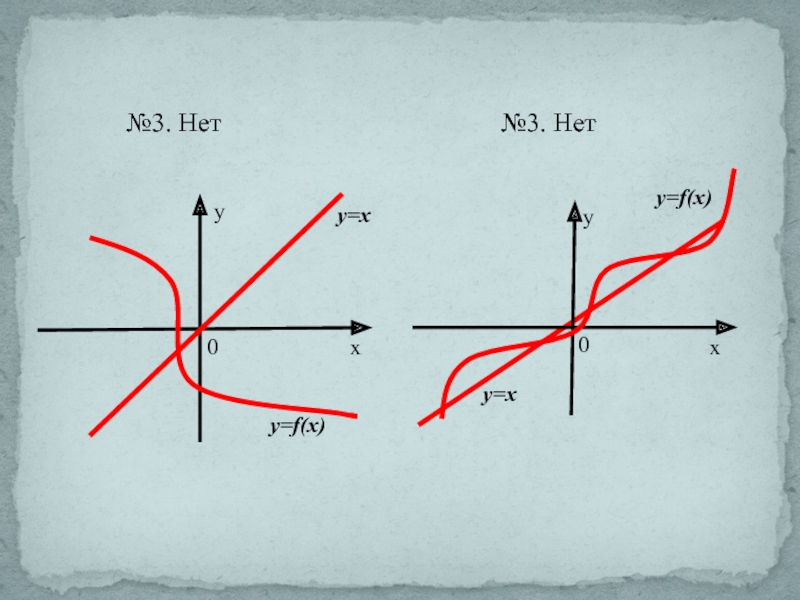
- 5. №3. На рисунке изображен график функции у=f(х),
- 6. График четной функции симметричен относительно оси ординат.Функция
- 7. График нечетной функции симметричен относительно начала координат.Функция
- 8. № 1. Какое значение принимает производная функции
- 9. №2. Назовите промежутки возрастания функции№2. Назовите промежутки убывания функцииОтвет: 1. 0
- 10. №3 Функция y=f(x) определена на промежутке (-3;4).
- 11. №4 Функция y=f(x) определена на промежутке (-3;4).
- 12. Вариант 2Вариант 1№1. Да(f( х)+g(х))/= f/( х) + g/(х)№1. Да(f( х)-g(х))/= f/( х) - g/(х)
- 13. №2. Нет№2. Даy=f(x)
- 14. №3. Нет№3. Нет
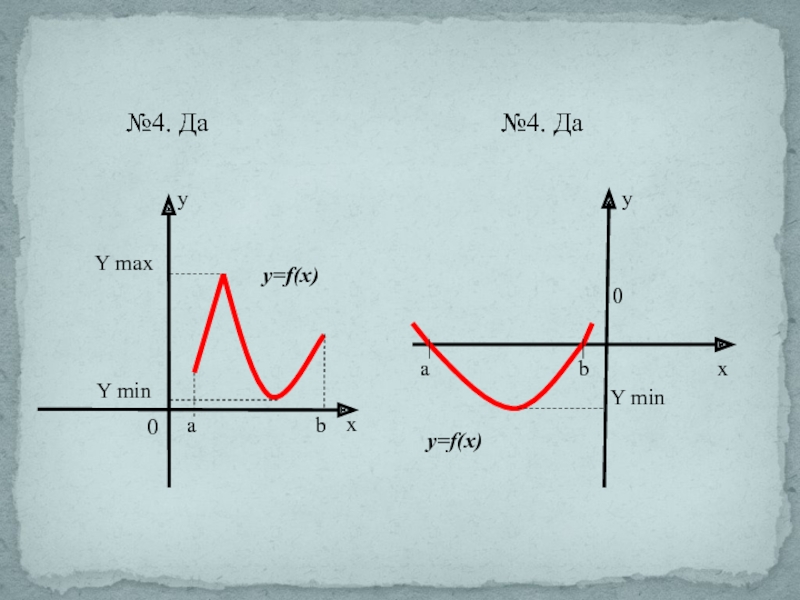
- 15. №4. Да№4. Да
- 16. Пусть АD = х, тогда
- 17. Пусть АD = х, тогда №5. Да
- 18. Итог урока: что мы должны знатьОсновные правила
- 19. Домашнее задание:Тест по теме: «Производная и ее применение»
Слайд 1Алгебра и начала анализа 11 класс
Производная и ее применения
Урок обобщения и
Слайд 2Определение производной
Основные правила дифференцирования и формулы производных функций
Геометрический смысл производной и
Исследование функций с помощью производной
Задачи урока
Повторить и закрепить
Слайд 5№3. На рисунке изображен график функции у=f(х), заданный на отрезке [a;b]
Найдите: а) точки максимума и минимума;
б) точки, в которых функция
принимает наибольшее и
наименьшее значения
на отрезке [a;b].
Слайд 6График четной функции симметричен относительно оси ординат.
Функция возрастает на некотором промежутке,
Точка х0 называется точкой максимума функции f(х), если для всех х≠х0 из некоторой окрестности точки х0 выполняется неравенство f(x)
Геометрический смысл производной заключается в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в данной точке.
Вариант 1
Слайд 7График нечетной функции симметричен относительно начала координат.
Функция убывает на некотором промежутке,
Точка х0 называется точкой минимума функции f(х), если для всех х≠х0 из некоторой окрестности точки х0 выполняется неравенство f (x)> f(х0)
Для того чтобы точка х0 была точкой экстремума функции f(х), необходимо, чтобы эта точка была критической для данной функции.
Пусть функция f(х) определена в некоторой окрестности х0 и дифференцируема в этой точке. Если х0 – точка экстремума функции f(х), то f’(x)=0.
Вариант 2
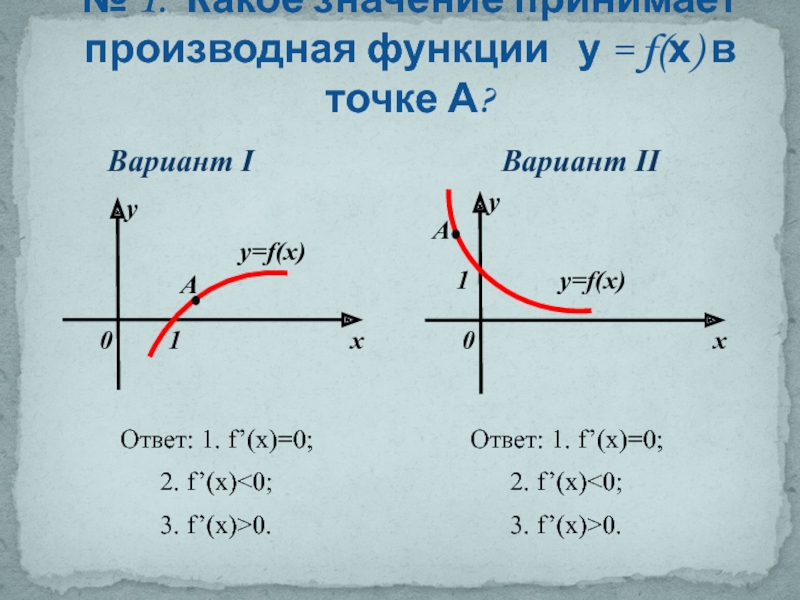
Слайд 8№ 1. Какое значение принимает производная функции у = f(х)
Вариант II
Вариант I
Ответ: 1. f’(x)=0;
2. f’(x)<0;
3. f’(x)>0.
Ответ: 1. f’(x)=0;
2. f’(x)<0;
3. f’(x)>0.
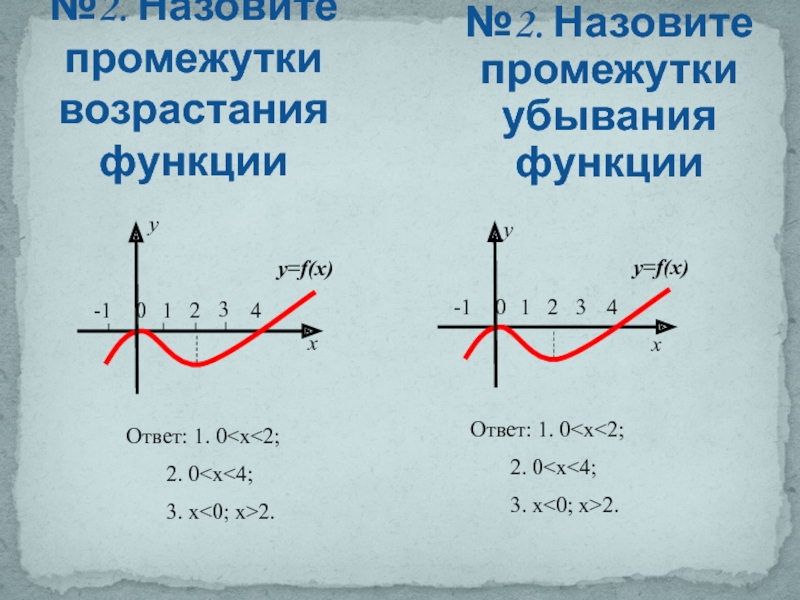
Слайд 9№2. Назовите промежутки возрастания функции
№2. Назовите промежутки убывания функции
Ответ: 1. 0
Ответ: 1. 0
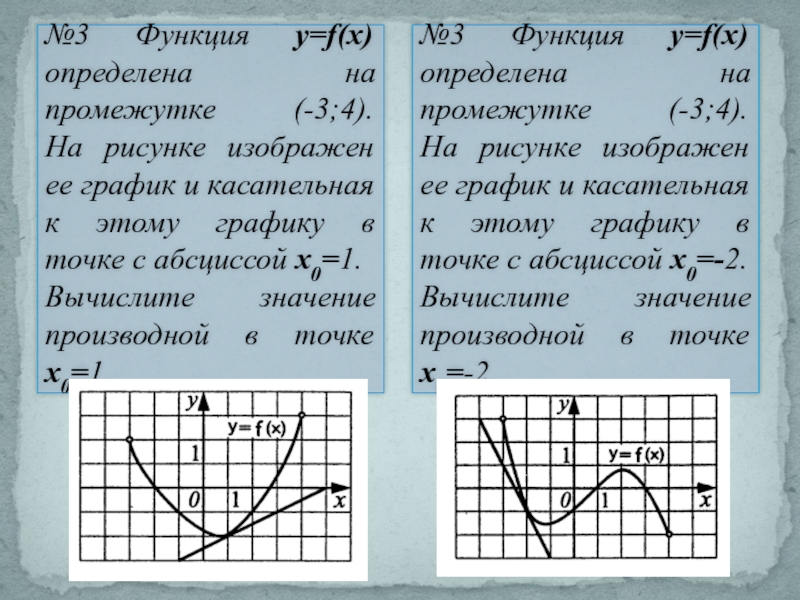
Слайд 10№3 Функция y=f(x) определена на промежутке (-3;4). На рисунке изображен ее график
Вычислите значение производной в точке х0=-2.
№3 Функция y=f(x) определена на промежутке (-3;4).
На рисунке изображен ее график и касательная к этому графику в точке с абсциссой х0=1.
Вычислите значение производной в точке х0=1.
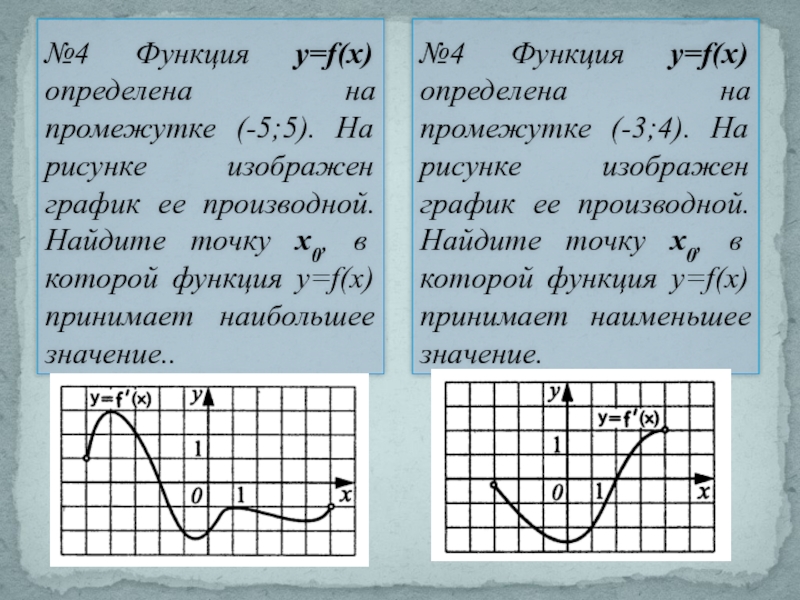
Слайд 11№4 Функция y=f(x) определена на промежутке (-3;4). На рисунке изображен график
№4 Функция y=f(x) определена на промежутке (-5;5). На рисунке изображен график ее производной. Найдите точку х0, в которой функция y=f(x) принимает наибольшее значение..
Слайд 18Итог урока:
что мы должны знать
Основные правила дифференцирования;
Формулы производных элементарных функций;
Геометрический
Уравнение касательной;
Применение производной к исследованию функций.




![Презентация Производная и ее применение. №3. На рисунке изображен график функции у=f(х), заданный на отрезке [a;b] №3. На рисунке изображен график функции у=f(х), заданный на отрезке [a;b] Найдите: а) точки максимума и минимума;б)](/img/thumbs/bb4aa891c111c8975ff0c55d04b95bac-800x.jpg)