- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Задачи на разрезание
Содержание
- 1. Презентация по теме Задачи на разрезание
- 2. I. Историческая справкаПервый трактат, в котором рассматриваются
- 3. II. Задачи на клетчатой бумагеЗадача №1. Квадрат
- 4. Задача №2.Прямоугольник 3 x 5 содержит 15
- 5. Задача №3.Разделите квадрат 4 х 4 на
- 6. Задача №4.Разделите фигуру на три равные части так, чтобы линия разреза шла по сторонам квадратов.Решение:
- 7. Задача №5.Разделите фигуру на четыре равные части
- 8. Задача №6.Разрежьте фигуры, на две равные части
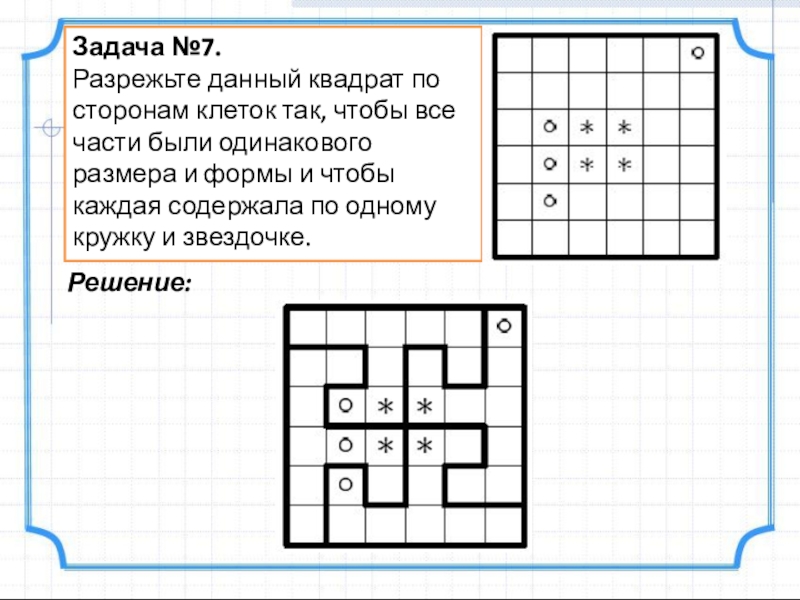
- 9. Задача №7.Разрежьте данный квадрат по сторонам клеток
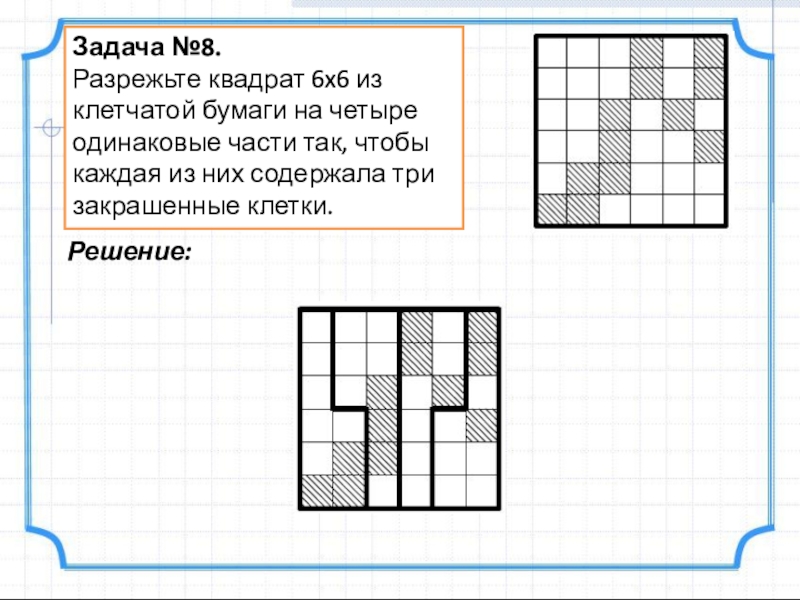
- 10. Задача №8.Разрежьте квадрат 6x6 из клетчатой бумаги
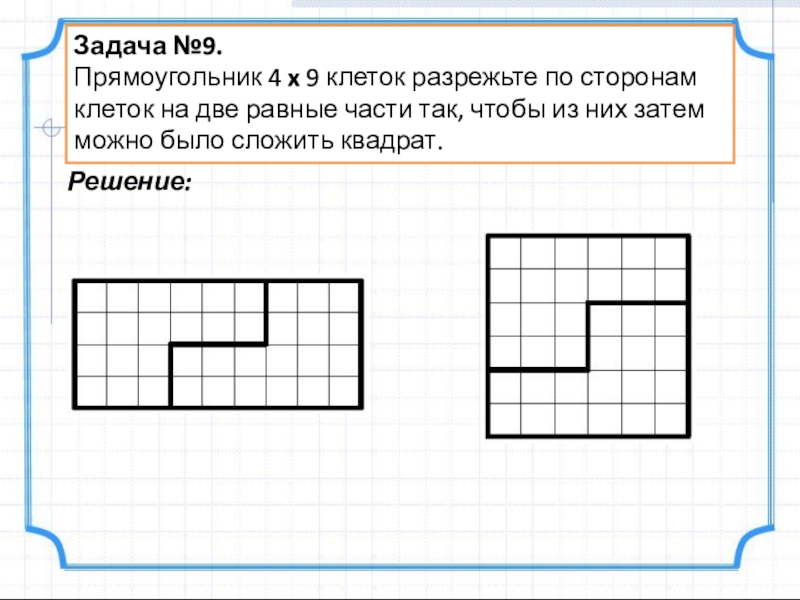
- 11. Задача №9.Прямоугольник 4 x 9 клеток разрежьте
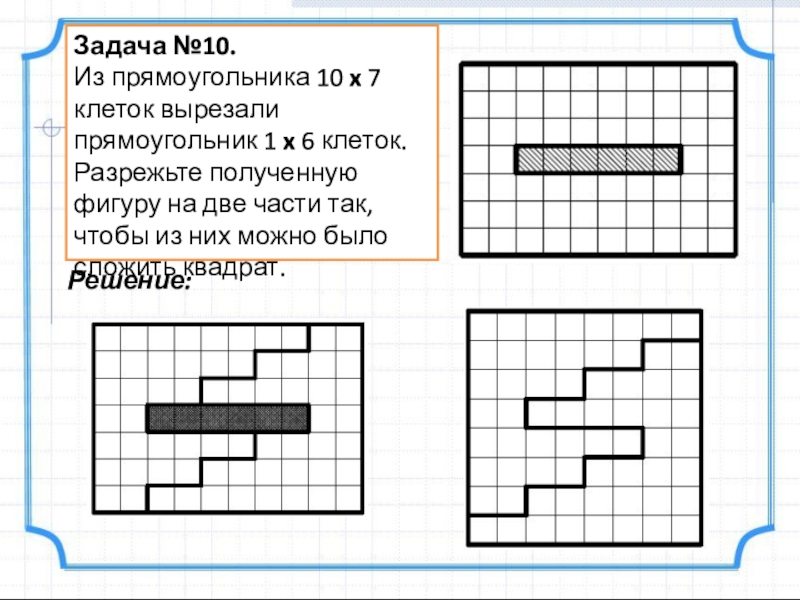
- 12. Задача №10.Из прямоугольника 10 x 7 клеток
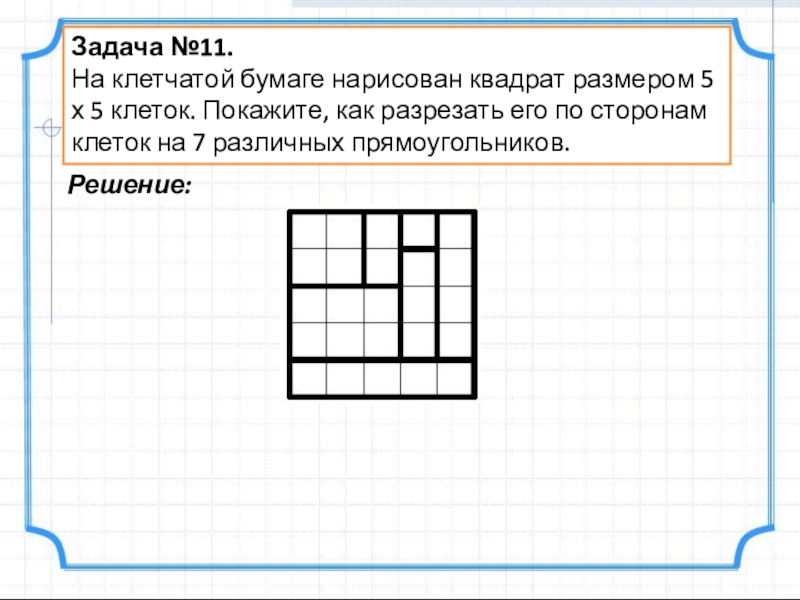
- 13. Задача №11.На клетчатой бумаге нарисован квадрат размером
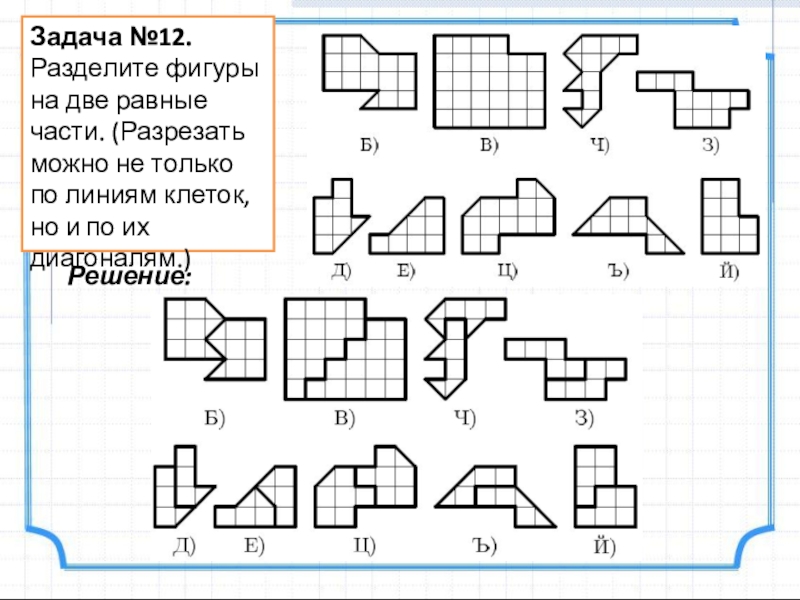
- 14. Задача №12.Разделите фигуры на две равные части.
- 15. III. ПентаминоФигуры:ДоминоТриминоТетрамино Пентамино Составляют из двух, трех,
- 16. Задача №13.Составьте всевозможные фигуры тетрамино (от греч.
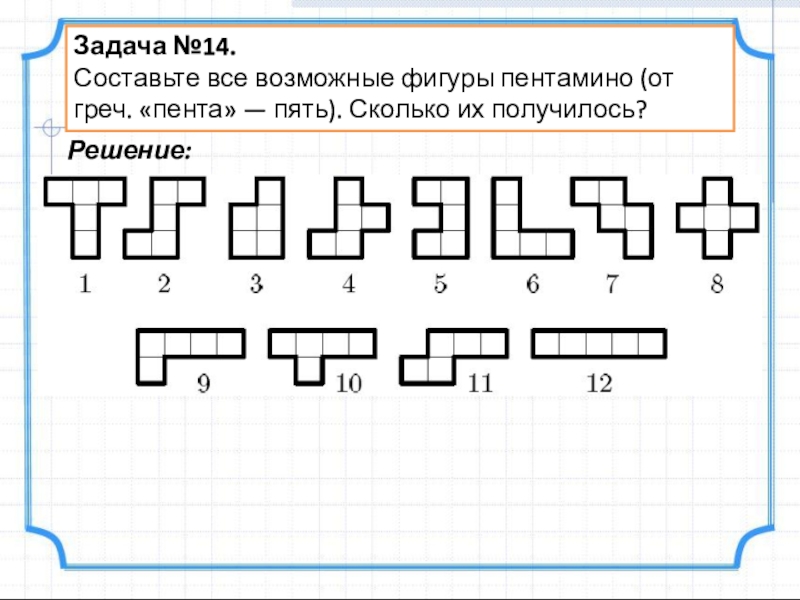
- 17. Задача №14.Составьте все возможные фигуры пентамино (от греч. «пента» — пять). Сколько их получилось?Решение:
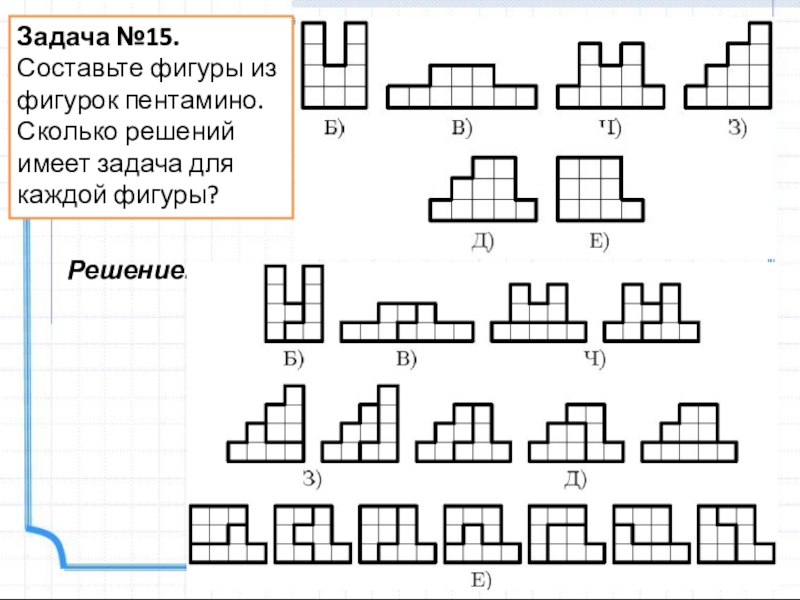
- 18. Задача №15.Составьте фигуры из фигурок пентамино. Сколько решений имеет задача для каждой фигуры?Решение:
- 19. Фигура 1 обладает следующим свойством. Если ее
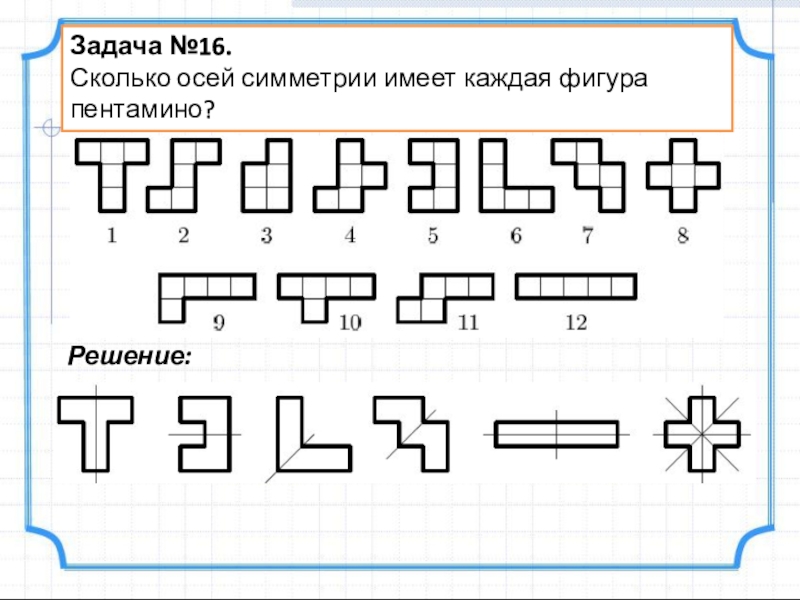
- 20. Задача №16.Сколько осей симметрии имеет каждая фигура пентамино?Решение:
- 21. Домашнее задание*
Слайд 1«Геометрия является самым могущественным средством для изощрения наших умственных способностей и
Галилео Галилей
Слайд 2I. Историческая справка
Первый трактат, в котором рассматриваются задачи на разрезание.
Известными специалистами
Слайд 3II. Задачи на клетчатой бумаге
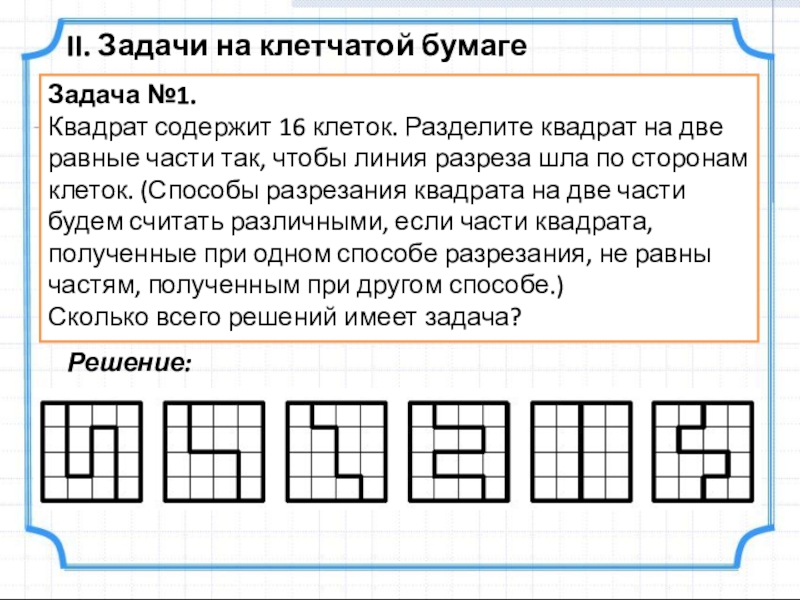
Задача №1.
Квадрат содержит 16 клеток. Разделите
Сколько всего решений имеет задача?
Решение:
Слайд 4Задача №2.
Прямоугольник 3 x 5 содержит 15 клеточек и центральная клетка
Решение:
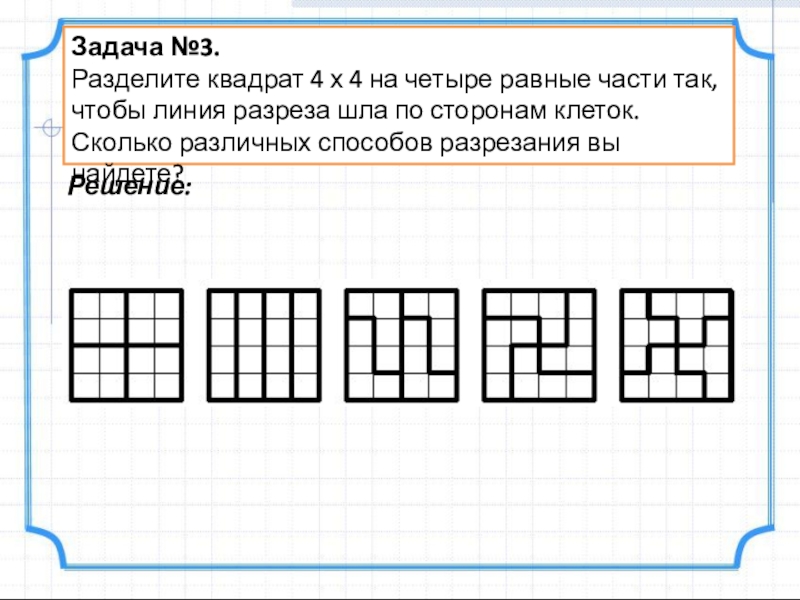
Слайд 5Задача №3.
Разделите квадрат 4 х 4 на четыре равные части так,
Решение:
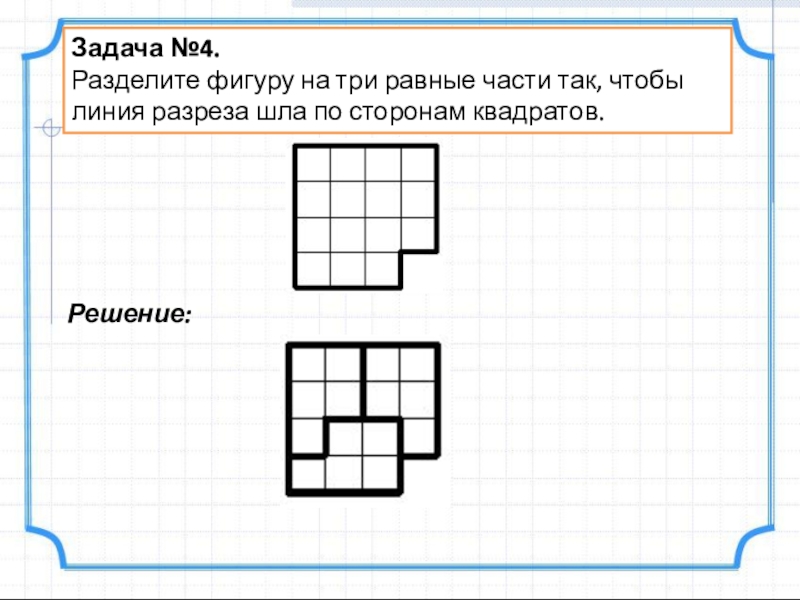
Слайд 6Задача №4.
Разделите фигуру на три равные части так, чтобы линия разреза
Решение:
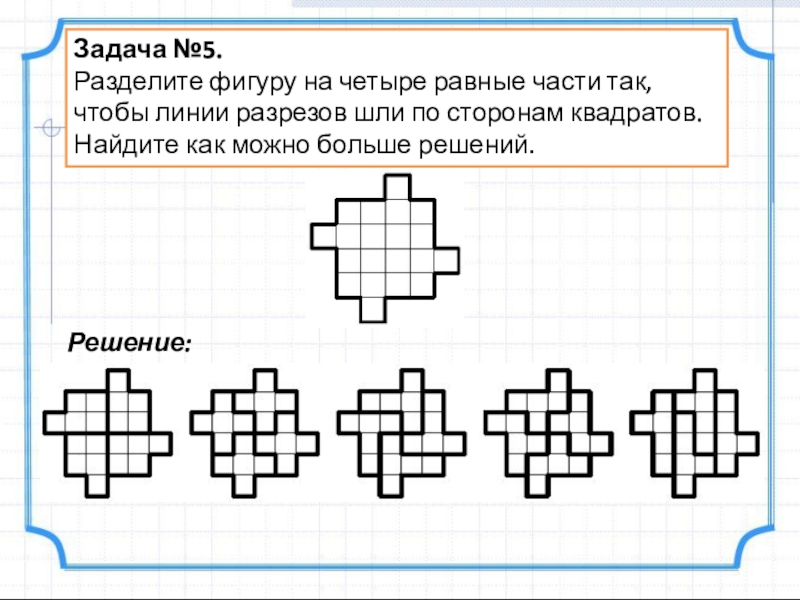
Слайд 7Задача №5.
Разделите фигуру на четыре равные части так, чтобы линии разрезов
Решение:
Слайд 8Задача №6.
Разрежьте фигуры, на две равные части по линиям сетки, причем
Решение:
Слайд 9Задача №7.
Разрежьте данный квадрат по сторонам клеток так, чтобы все части
Решение:
Слайд 10Задача №8.
Разрежьте квадрат 6x6 из клетчатой бумаги на четыре одинаковые части
Решение:
Слайд 11Задача №9.
Прямоугольник 4 x 9 клеток разрежьте по сторонам клеток на
Решение:
Слайд 12Задача №10.
Из прямоугольника 10 x 7 клеток вырезали прямоугольник 1 x
Решение:
Слайд 13Задача №11.
На клетчатой бумаге нарисован квадрат размером 5 х 5 клеток.
Решение:
Слайд 14Задача №12.
Разделите фигуры на две равные части. (Разрезать можно не только
Решение:
Слайд 15III. Пентамино
Фигуры:
Домино
Тримино
Тетрамино
Пентамино
Составляют из двух, трех, четырех, пяти квадратов так,
Из двух одинаковых квадратов можно составить только одну фигуру — домино.
Фигуры тримино можно получить из единственной фигуры домино, приставляя к ней различными способами еще один квадрат. Получится две фигуры тримино.
Слайд 16Задача №13.
Составьте всевозможные фигуры тетрамино (от греч. слова «тетра» — четыре).
Решение:
Слайд 17Задача №14.
Составьте все возможные фигуры пентамино (от греч. «пента» — пять).
Решение:
Слайд 18Задача №15.
Составьте фигуры из фигурок пентамино. Сколько решений имеет задача для
Решение:
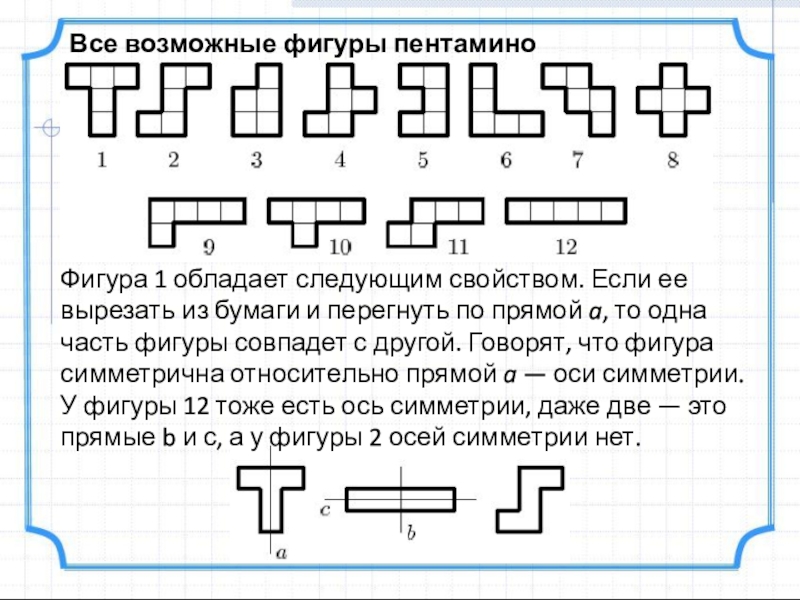
Слайд 19Фигура 1 обладает следующим свойством. Если ее вырезать из бумаги и
У фигуры 12 тоже есть ось симметрии, даже две — это прямые b и с, а у фигуры 2 осей симметрии нет.
Все возможные фигуры пентамино