Д. А.
Проверила:
Короваева С. В.
Хабаровск, 2017
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме способы умножения натуральных чисел внеурочная деятельность
Содержание
- 1. Презентация по теме способы умножения натуральных чисел внеурочная деятельность
- 2. Цель: Ознакомление с различными способами умножения натуральных
- 3. Задачи: 1.Найти и разобрать различные способы умножения.2.Научиться
- 4. Гипотеза: Надо ли знать таблицу умножения?
- 5. Актуальность: В последнее время ребята всё с
- 6. Содержание:1. Введение.
- 7. Введение.Аще кто не твердит Таблицы и гордит,
- 8. Русско-крестьянский способ умножения. Сущность его в том,
- 9. Пример: 32 х 13 Ясно поэтому, что
- 10. "А как быть с нечетными числами, которые не кратны 2-м?".
- 11. Итак, пусть нам необходимо умножить два числа:
- 12. 1998+3996+15984+31968+127872+255744++511488+1022976=1972026Искомое произведение: 1972026
- 13. Квадрат Пифагора.1 2 34 5 67 8 9
- 14. 1 2
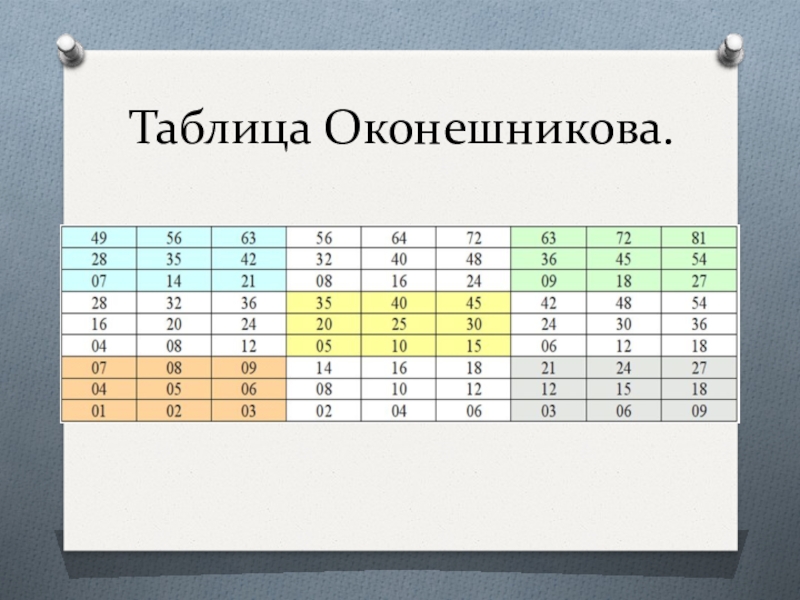
- 15. Таблица Оконешникова.
- 16. Пример: 15647 х 5
- 17. Индийский способ умножения.Умножаем, например, числа 6827 и
- 18. Египетский способ умножения.Чтобы правильно подобрать кратное число,
- 19. Пример разложения числа 25:Кратный множитель для числа
- 20. Пример: умножим «13» на «238» .Известно, что
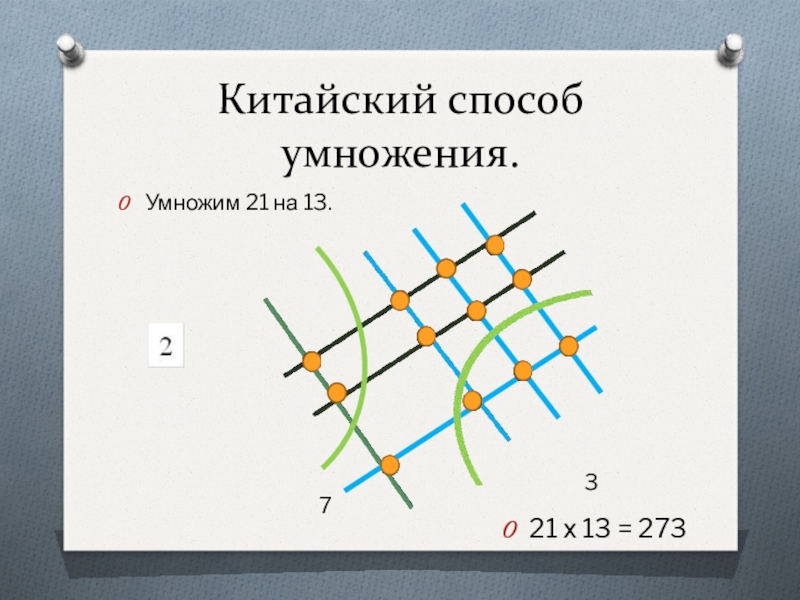
- 21. Китайский способ умножения.Умножим 21 на 13. 21 х 13 = 273 73
- 22. Японский способ умножения.Японский способ умножения – это
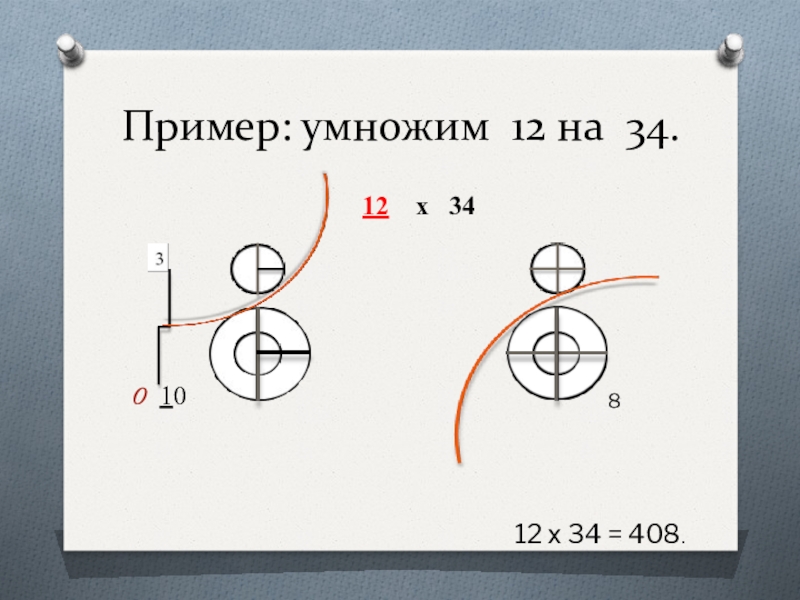
- 23. Пример: умножим 12 на 34. 12 х 34 10812 х 34 = 408.
- 24. Метод Ферроля.Например: 12х14=168а) 2х4=8, пишем 8б) 1х4+2х1=6, пишем 6в) 1х1=1, пишем 1.
- 25. Старинный способ умножения на 9 на пальцах.Это
- 26. Умножение двухзначных чисел на 11. При умножении
- 27. Умножение на число 142857.При умножении числа 142857
- 28. Умножение на число 37037 При умножении числа
- 29. Умножение двухзначных чисел, близких к 100.Пример: 94
- 30. Деление.На самом деле старинных способов умножения практически
- 31. ЗаключениеСтаринные способы умножения и деления неуклюжи и
- 32. Литература1.Гейзер Г.И. История математики в школе, VII-VII
Цель: Ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Слайд 1Проект:
«Способы умножения натуральных чисел»
Подготовили:
Ученицы 6 «А» класса
МБОУ гимназии №1
Арутюнян Л. А.
Ушакова
Слайд 2Цель:
Ознакомление с различными способами умножения натуральных чисел, не используемых на
уроках, и их применение при вычислениях числовых выражений.
Слайд 3Задачи:
1.Найти и разобрать различные способы умножения.
2.Научиться демонстрировать некоторые способы умножения.
3.Рассказать
о новых способах умножения и научить ими пользоваться учащихся.
4.Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.
4.Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.
Слайд 5Актуальность:
В последнее время ребята всё с большей неохотой относятся к
учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» мы выбрали тему нашего проекта «Способы умножения натуральных чисел».
Слайд 6Содержание:
1. Введение.
2. Основная часть.
2.1.Русско-крестьянский способ умножения.
2.2.Квадрат Пифагора.
2.3.Таблица Оконешникова.
2.4.Индийский способ умножения.
2.5.Египетский способ умножения.
2.6. Китайский способ умножения.
2.7.Японский способ умножения.
2.8.Метод Ферроля.
2.9.Старинный способ Умножение на 9 на пальцах.
2.10.Умножение двухзначных чисел на 11.
2.11.Умножение на число 142857.
2.12.Умножение на число 37037.
2.13.Умножение двухзначных чисел, близких к 100.
3. Деление.
4. Заключение.
5.Литература.
Слайд 7Введение.
Аще кто не твердит
Таблицы и гордит,
Не может познати
Числом
что множати
И во всей науки, несвобод от муки,
Колико не учиттуне ся удручит
И в пользу не будет аще ю забудет.
И во всей науки, несвобод от муки,
Колико не учиттуне ся удручит
И в пользу не будет аще ю забудет.
Слайд 8Русско-крестьянский способ умножения.
Сущность его в том, что умножение любых двух чисел
сводится к ряду последовательных делений одного числа пополам при одновременном удвоений другого числа.
Слайд 9Пример: 32 х 13
Ясно поэтому, что в результате многократного повторения
этой операции получается искомое произведение:
( 32 х 13 ) = ( 1 х 416 )
( 32 х 13 ) = ( 1 х 416 )
Слайд 11Итак, пусть нам необходимо умножить два числа: 987и 1998.
987 1998
493 3996
246 7992
123 15984
61 31968
30 63936
15 127872
7 255744
3 511488
1 1022976
493 3996
246 7992
123 15984
61 31968
30 63936
15 127872
7 255744
3 511488
1 1022976
Слайд 141 2
3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
10 20 30 40 50 60 70 80 90
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
10 20 30 40 50 60 70 80 90
Слайд 17Индийский способ умножения.
Умножаем, например, числа 6827 и 345:
Посмотри, как из результатов
сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315
Слайд 18Египетский способ умножения.
Чтобы правильно подобрать кратное число, нужно было знать следующую
таблицу значений:
1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32
1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32
Слайд 19Пример разложения числа 25:
Кратный множитель для числа «25» — это 16;
25 — 16 = 9. Кратный множитель для числа «9» — это 8; 9 — 8 = 1. Кратный множитель для числа «1» — это 1; 1 — 1 = 0. Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1.
Слайд 20Пример: умножим «13» на «238» .
Известно, что 13 = 8 +
4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: ✔ 1 х 238 = 238 ✔ 4 х 238 = 952 ✔ 8 х 238 = 1904
13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 1904 + 952 + 238 = =3094.
13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 1904 + 952 + 238 = =3094.
Слайд 22Японский способ умножения.
Японский способ умножения – это графический способ с использованием
кругов и линий. Не менее забавный и интересный чем китайский. Даже чем-то на него похож.
Слайд 25Старинный способ умножения на 9 на пальцах.
Это просто. Чтобы умножить любое
число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
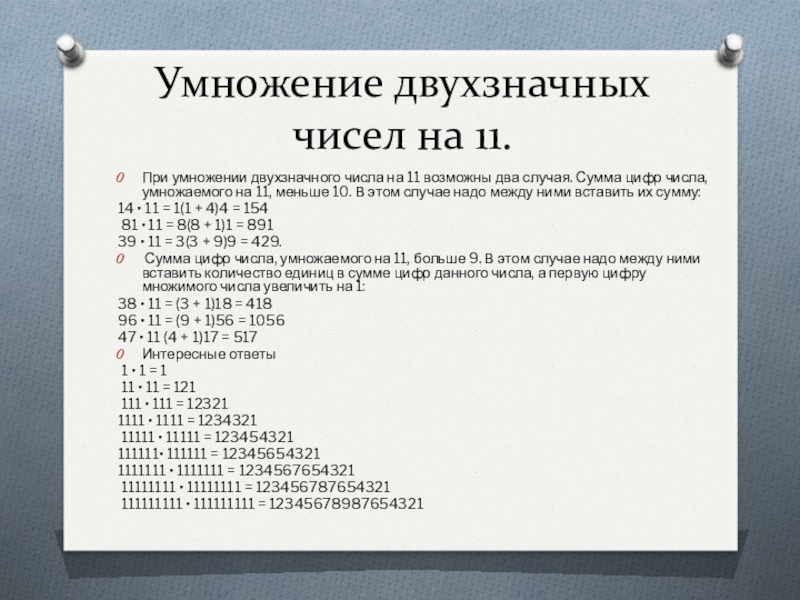
Слайд 26Умножение двухзначных чисел на 11.
При умножении двухзначного числа на 11
возможны два случая. Сумма цифр числа, умножаемого на 11, меньше 10. В этом случае надо между ними вставить их сумму:
14 • 11 = 1(1 + 4)4 = 154
81 • 11 = 8(8 + 1)1 = 891
39 • 11 = 3(3 + 9)9 = 429.
Сумма цифр числа, умножаемого на 11, больше 9. В этом случае надо между ними вставить количество единиц в сумме цифр данного числа, а первую цифру множимого числа увеличить на 1:
38 • 11 = (3 + 1)18 = 418
96 • 11 = (9 + 1)56 = 1056
47 • 11 (4 + 1)17 = 517
Интересные ответы
1 • 1 = 1
11 • 11 = 121
111 • 111 = 12321
1111 • 1111 = 1234321
11111 • 11111 = 123454321
111111• 111111 = 12345654321
1111111 • 1111111 = 1234567654321
11111111 • 11111111 = 123456787654321
111111111 • 111111111 = 12345678987654321
14 • 11 = 1(1 + 4)4 = 154
81 • 11 = 8(8 + 1)1 = 891
39 • 11 = 3(3 + 9)9 = 429.
Сумма цифр числа, умножаемого на 11, больше 9. В этом случае надо между ними вставить количество единиц в сумме цифр данного числа, а первую цифру множимого числа увеличить на 1:
38 • 11 = (3 + 1)18 = 418
96 • 11 = (9 + 1)56 = 1056
47 • 11 (4 + 1)17 = 517
Интересные ответы
1 • 1 = 1
11 • 11 = 121
111 • 111 = 12321
1111 • 1111 = 1234321
11111 • 11111 = 123454321
111111• 111111 = 12345654321
1111111 • 1111111 = 1234567654321
11111111 • 11111111 = 123456787654321
111111111 • 111111111 = 12345678987654321
Слайд 27Умножение на число 142857.
При умножении числа 142857 на числа от 1
до 6 получается произведение, записанное теми же цифрами, переставленными в циклическом порядке: 142857 • 1 = 142857;
142857 • 2 = 285714;
142857 • 3 = 428571;
142857 • 4 = 571428;
142857 • 5 = 714285;
142857 • 6 = 857142.
142857 • 2 = 285714;
142857 • 3 = 428571;
142857 • 4 = 571428;
142857 • 5 = 714285;
142857 • 6 = 857142.
Слайд 28Умножение на число 37037
При умножении числа 37037 на числа от
1 до 9 получается произведение, записанное периодическими цифрами. Затем полученное число умножьте на 3.
37037 • 1 = 37037
37037 • 2 = 74074
37037 • 3 = 111111
37037 • 4 = 148148
37037 • 5 = 185185
37037 • 6 = 222222
37037 • 7 = 259259
37037 • 8 = 296296
37037 • 9 = 333333
37037 • 1 = 37037
37037 • 2 = 74074
37037 • 3 = 111111
37037 • 4 = 148148
37037 • 5 = 185185
37037 • 6 = 222222
37037 • 7 = 259259
37037 • 8 = 296296
37037 • 9 = 333333
Слайд 29Умножение двухзначных чисел, близких к 100.
Пример: 94 • 78
Решение: чтобы
получить необходимые последние цифры (единицы и десятки), необходимо: 100 – 94 = 6 ,100 – 78 = 22 и результаты перемножить 6 · 22 = 132 32 последние две цифры (1 запоминаем) Чтобы получить первые две цифры (тысячи и сотни), надо: 94 – 22 = 72 72+1 = 73 В результате имеем 94•78 = 7332
Слайд 30Деление.
На самом деле старинных способов умножения практически не осталось. Но мы
бы хотели поделиться с одним облегчавшим ваши действия при делении методом.
Если делитель является составным числом, то разлагаем его на два или более множителей, а потом выполняем последовательное деление.
Например :
720:45=(720:9):5=80:5=16
Если делитель является составным числом, то разлагаем его на два или более множителей, а потом выполняем последовательное деление.
Например :
720:45=(720:9):5=80:5=16
Слайд 31Заключение
Старинные способы умножения и деления неуклюжи и неудобны, но так ли
хорош наш нынешний способ, чтобы в нем невозможны были уже никакие дальнейшие улучшения? Нет, и наш способ не является совершенным; можно придумать еще более быстрые или еще более надежные. Современный способ деления, использующий частичные произведения делителя на отдельные разряды частного (деление столбиком), представлен в итальянском манускрипте 1460 года. Таким образом, цель работы достигнута. Данное исследование можно использовать для проведения математических кружков и факультативов, для подготовки учащихся к математическим олимпиадам и турнирам.
Слайд 32Литература
1.Гейзер Г.И. История математики в школе, VII-VII классы. Пособие для учителя.
- М.: Просвещение, 1982
2.Игнатьев Е.И. Математическая шкатулка. Занимательные задачи, игры, фокусы, парадоксы. - М.:, Омега, 1994
3.Депнам И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5-6 кл. сред. кл. - М.: Просвещение, 1989
4.Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
5.Перельман Я.И. Занимательная арифметика. М.Русанова,1994--205с.
6.Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.
2.Игнатьев Е.И. Математическая шкатулка. Занимательные задачи, игры, фокусы, парадоксы. - М.:, Омега, 1994
3.Депнам И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5-6 кл. сред. кл. - М.: Просвещение, 1989
4.Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
5.Перельман Я.И. Занимательная арифметика. М.Русанова,1994--205с.
6.Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.