прекрасны.
Платон
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Осевая симметрия , математика 6 класс
Содержание
- 1. Презентация по теме Осевая симметрия , математика 6 класс
- 2. Слайд 2
- 3. Слайд 3
- 4. Учитель математики: Кабанова С. А.
- 5. «… быть прекрасным значит быть симметричным и
- 6. № 309. Построение точки, симметричной даннойМсМ,1.
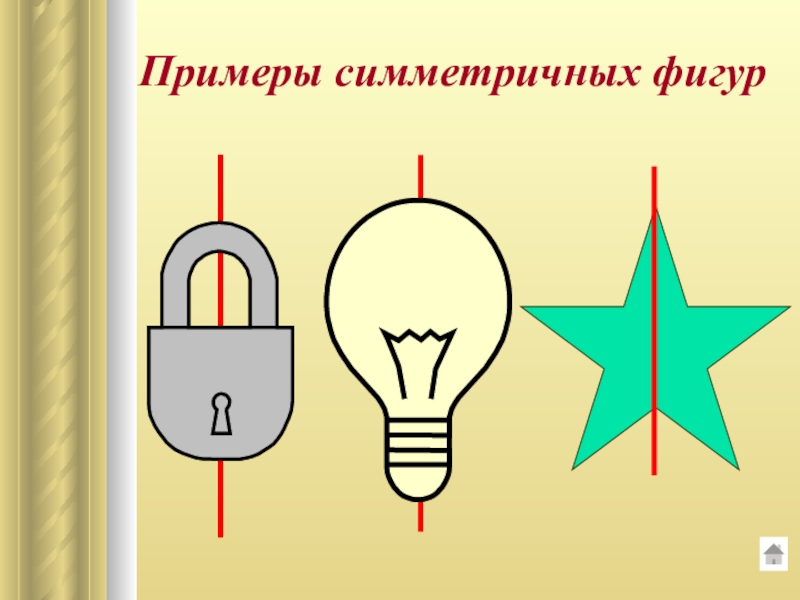
- 7. Примеры симметричных фигур
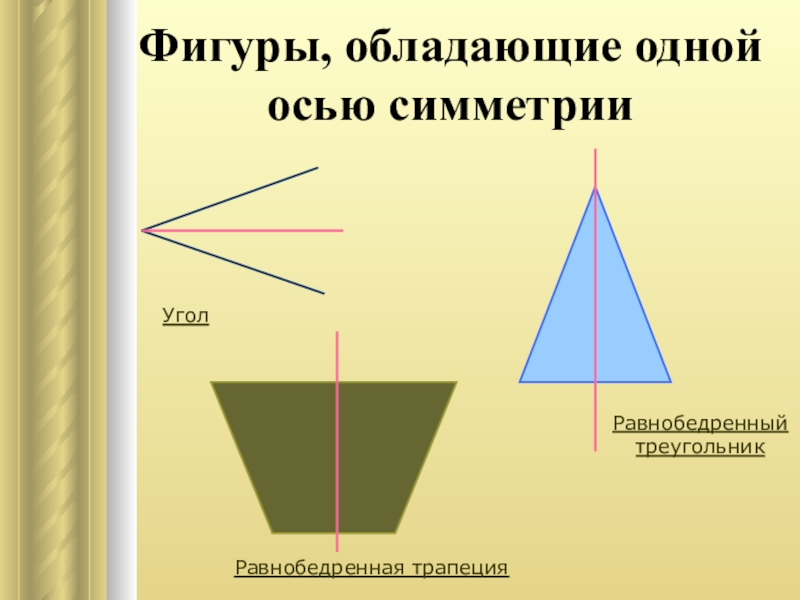
- 8. Фигуры, обладающие одной осью симметрииРавнобедренная трапецияРавнобедренный треугольникУгол
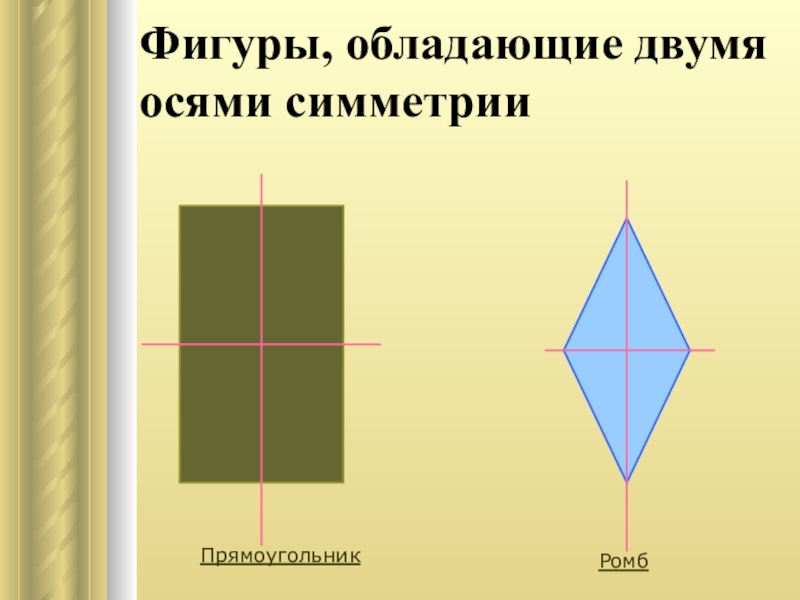
- 9. Фигуры, обладающие двумя осями симметрииПрямоугольникРомб
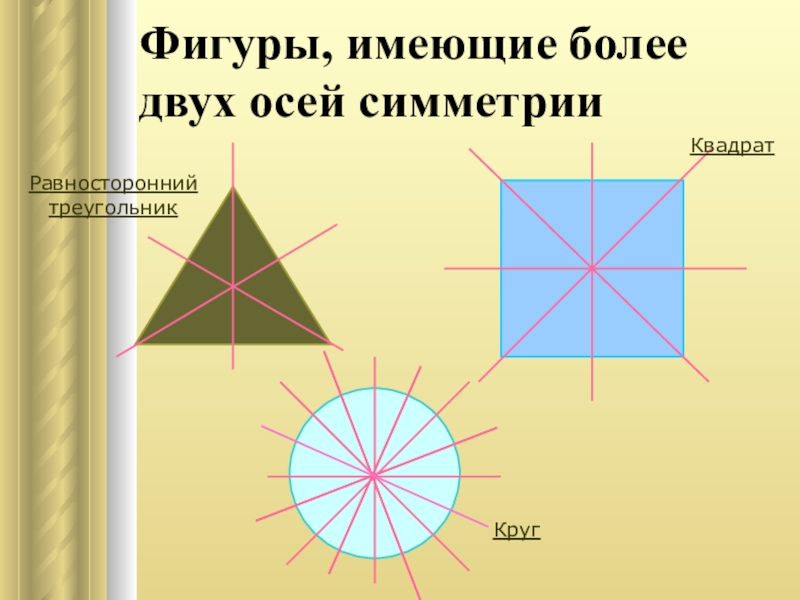
- 10. Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг
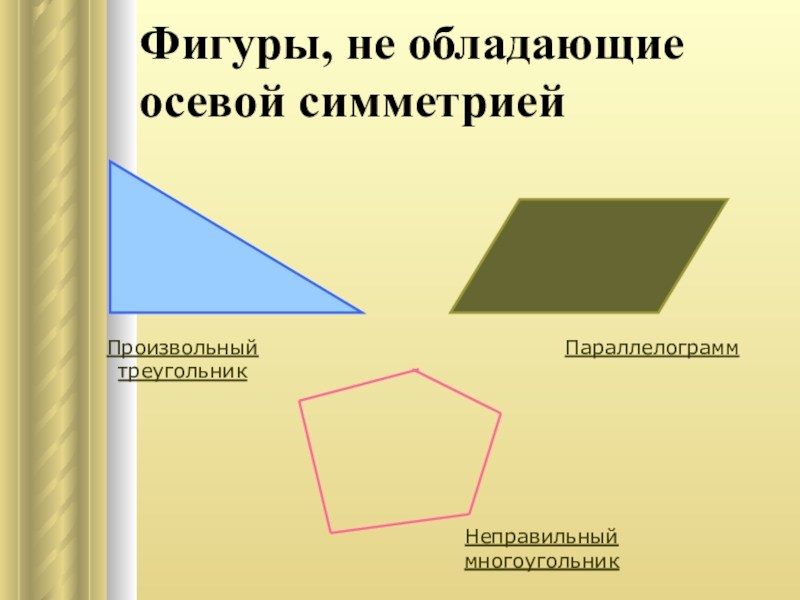
- 11. Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник
- 12. Симметрия в природеВнимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.
- 13. Зеркальная симметрия
- 14. Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
- 15. Симметрия в животном мире.
- 16. В узорах знаменитых павловопосадских платков сочетание повторяющихся элементов.
- 17. Симметрия в архитектуре
- 18. Пирамида Хеопса ЕгипетСобор Парижской Богоматери ФранцияТадж Махал ТурцияБиг Бэн ВеликобританияЭйфелева Башня
- 19. Слайд 19
- 20. Буквы русского языка тоже можно рассмотреть с
- 21. В русском языке есть «симметричные» слова –
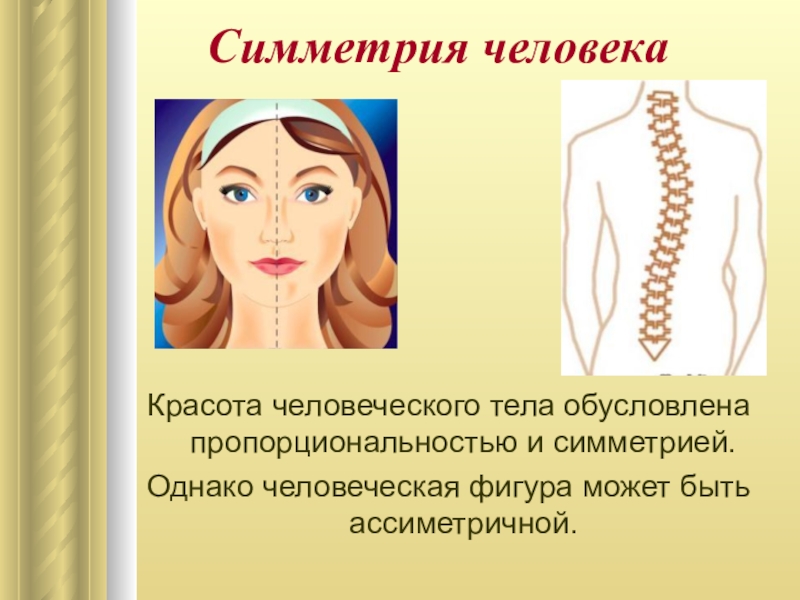
- 22. Симметрия человекаКрасота человеческого тела обусловлена пропорциональностью и симметрией. Однако человеческая фигура может быть ассиметричной.
- 23. Физкультминутка
- 24. Творческое задание.
- 25. Творческое задание.
- 26. 2. Придумайте рисунок, иллюстрирующий осевую симметрию и
- 27. Спасибо за урок!“Принцип симметрии охватывает все новые и новые области…”Вернадский В.И.
Учитель математики: Кабанова С. А. Тема урока «Осевая симметрия.» 6 класс
Слайд 5«… быть прекрасным
значит быть симметричным
и соразмерным»
Платон
Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.
Г. Вейль
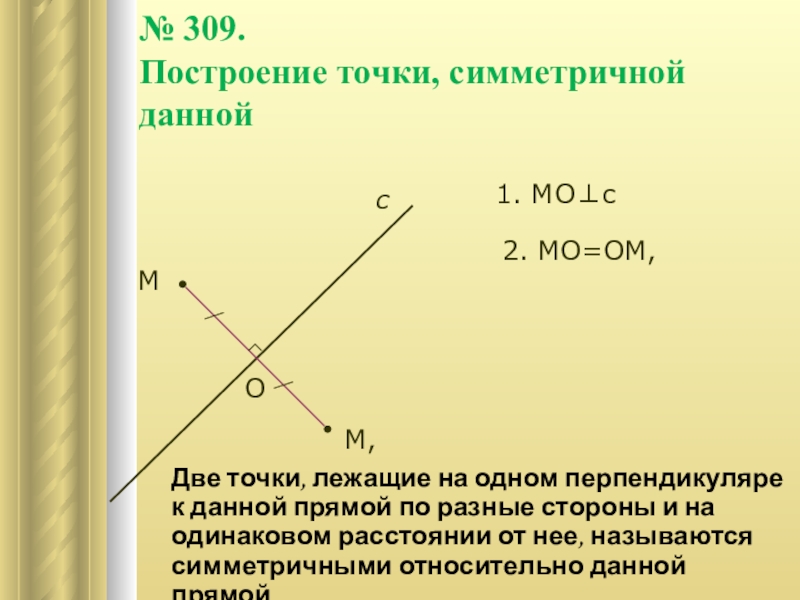
Слайд 6№ 309.
Построение точки, симметричной данной
М
с
М,
1. МОс
О
2. МО=ОМ,
Две точки, лежащие на
одном перпендикуляре к данной прямой по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно данной прямой.
Слайд 11Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
Слайд 12Симметрия в природе
Внимательное наблюдение показывает, что основу красоты многих форм, созданных
природой, составляет симметрия.
Слайд 18Пирамида Хеопса Египет
Собор Парижской Богоматери Франция
Тадж Махал Турция
Биг Бэн Великобритания
Эйфелева Башня
Слайд 20Буквы русского языка тоже можно рассмотреть с точки зрения симметрии.
Б;
Г; И; Й; Р; У; Ц; Ч; Щ; Я.
А; Д; Л; М; П; Т; Ф; Ш.
В; Е; З; К; С; Э; Ю.
Ж; Н; О; Х.
Вертикальная ось симметрии:
Горизонтальная ось симметрии:
И вертикальные и горизонтальные оси симметрии:
Нет ни вертикальной, ни горизонтальной оси:
Слайд 21В русском языке есть «симметричные» слова – палиндромы, которые можно читать
одинаково в двух направлениях:
шалаш, казак, радар,
Алла, Анна, кок, поп.
Могут быть палиндромическими
и предложения.
Написаны тысячи таких предложений.
А роза упала на лапу Азора.
Я иду с мечем судия.
(Г. Р. Державин.)
шалаш, казак, радар,
Алла, Анна, кок, поп.
Могут быть палиндромическими
и предложения.
Написаны тысячи таких предложений.
А роза упала на лапу Азора.
Я иду с мечем судия.
(Г. Р. Державин.)
Слайд 22Симметрия человека
Красота человеческого тела обусловлена пропорциональностью и симметрией.
Однако человеческая фигура
может быть ассиметричной.
Слайд 262. Придумайте рисунок, иллюстрирующий осевую симметрию и изобразите его на отдельном
листе.
Домашнее задание
Чтобы научиться думать, надо научиться придумывать.
Дж. Родари
№ 310 (вг), 316 (аг) ;
по желанию № 322 (аб)
