- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Комбинаторика
Содержание
- 1. Презентация по теме Комбинаторика
- 2. I. Основные комбинаторные правила
- 3. На теоретико-множественном языке:n(A) - число эл-ов множества
- 4. На теоретико-множественном языке:A × B – декартово
- 5. II. Соединения без повторений
- 6. Соединения n элементов из n с учётом
- 7. III. Соединения с повторениями
- 8. Упорядоченные множества из n эл-ов, из которых
- 9. IV. Решение задачЗадача 1. Десять участников полуфинала
- 10. Задача 2. Из трех классов спортивной школы
- 11. Задача 3. В хоккейном турнире участвуют 6
- 12. Задача 4. Из 7 разноцветных карточек разрезной
- 13. Задача 5.Сколько экзаменационных комиссий, состоящих из 7
- 14. Задача 6. В ящике находится 20 деталей.
- 15. Задача 7.Собрание из 40 человек избирает председателя,
- 16. Задача 8. Из 10 роз и 8
- 17. Задача 9.Сколько существует различных семизначных телефонных номеров?
- 18. Задача 10.Сколько существует различных семизначных телефонных номеров,
- 19. Задача 11.Имеется 9 различных книг, четыре из
- 20. Задача 12.Сколько нужно взять элементов, чтобы число
- 21. Задача 13.Сколькими способами можно расположить в ряд
- 22. Задача 14.Сколькими способами можно переставить буквы в
- 23. Задача 15.В кондитерской имеется 5 разных сортов
- 24. Задача 16.Делится ли число 40! на: а)410 б)780Решение:а)40! Не делится на 410
- 25. Задача 16.Делится ли число 40! на: а)410 б)780Решение:б)40! Делится на 780Ответ: а) нет, б) да
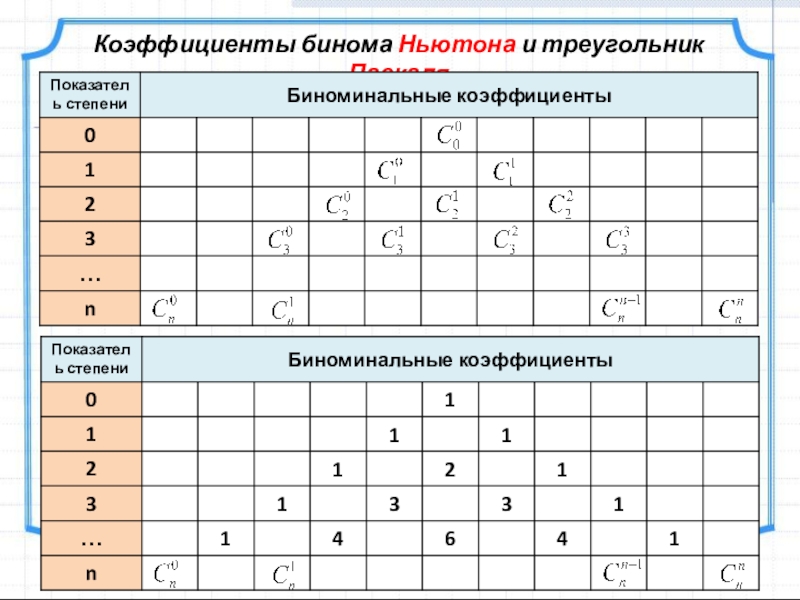
- 26. V. Биномиальная формула НьютонаБиномиальные коэффициенты
- 27. Коэффициенты бинома Ньютона и треугольник Паскаля
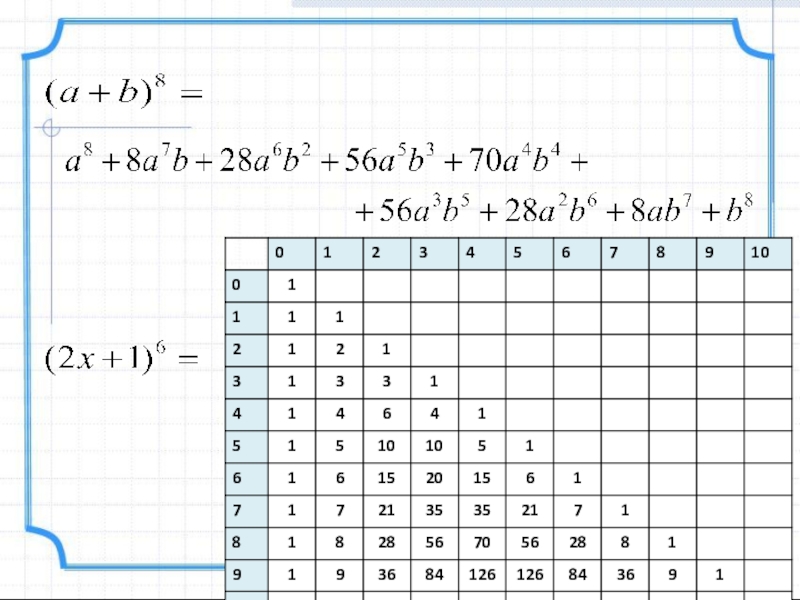
- 28. Слайд 28
- 29. Слайд 29
- 30. Домашнее задание*1_Комбинаторика [ДЗ].docДЗ
Слайд 1"Число, положение и комбинация – три взаимно пересекающиеся, но различные сферы
Слайд 3На теоретико-множественном языке:
n(A) - число эл-ов множества A,
n(B) - число
A ∪ B - объединение множеств A и B
Тогда для непересекающихся множеств A и B:
n(A ∪ B) = n(A) + n(B)
Правило суммы:
Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.
Пример №1. В первом ящике 8 шаров, во втором – 5. Сколько существует способов извлечь шар или из первого или из второго ящика.
Решение: 8 + 5 = 13 способов
Ответ: 13
Слайд 4На теоретико-множественном языке:
A × B – декартово произведение множеств A и
n(A × B) = n(A) · n(B)
Правило произведения:
Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m · k способами.
Пример №2. В первом ящике 8 шаров, во втором – 5. Сколько существует способов извлечь один шар из первого и один из второго ящика.
Решение: 8 · 5 = 40 способов
Ответ: 40
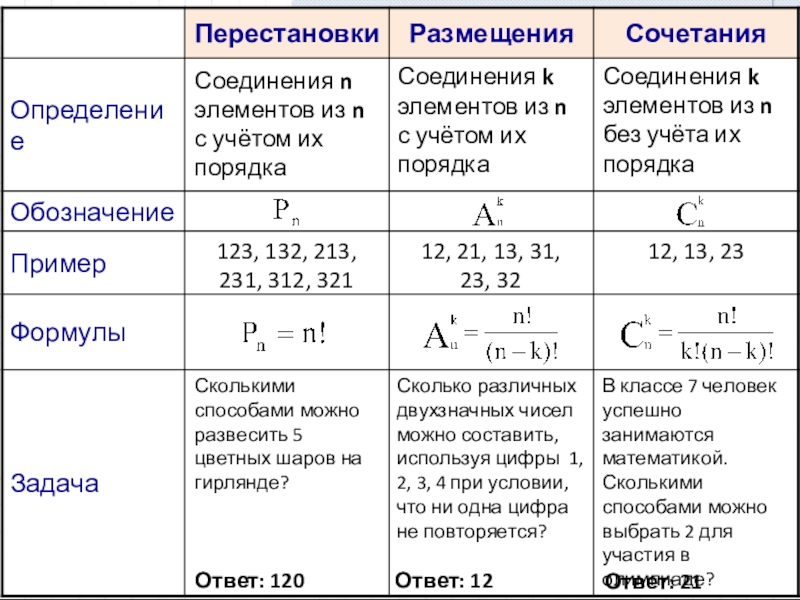
Слайд 6Соединения n элементов из n с учётом их порядка
Соединения k элементов
Соединения k элементов из n без учёта их порядка
123, 132, 213, 231, 312, 321
12, 21, 13, 31,
23, 32
12, 13, 23
Сколькими способами можно развесить 5 цветных шаров на гирлянде?
Ответ: 120
Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
Ответ: 12
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать 2 для участия в олимпиаде?
Ответ: 21
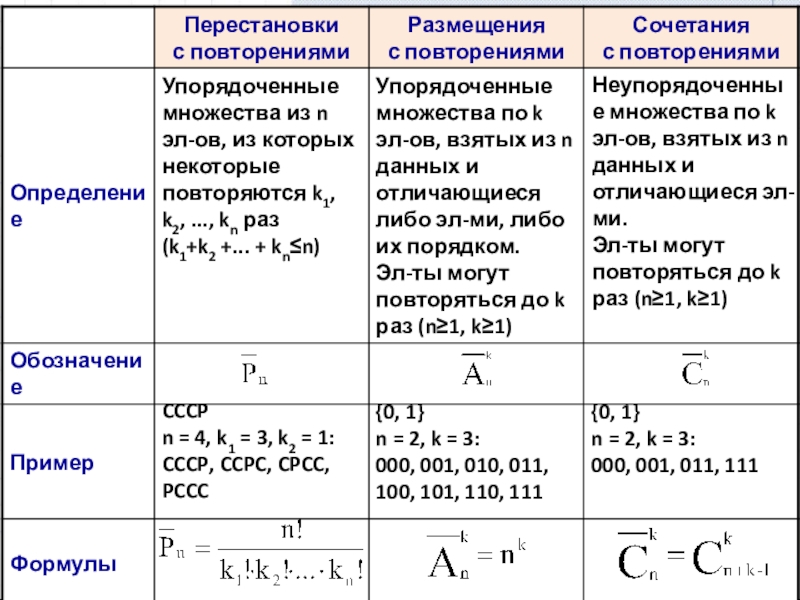
Слайд 8Упорядоченные множества из n эл-ов, из которых некоторые повторяются k1, k2,
Упорядоченные множества по k эл-ов, взятых из n данных и отличающиеся либо эл-ми, либо их порядком.
Эл-ты могут повторяться до k раз (n≥1, k≥1)
CCCP
n = 4, k1 = 3, k2 = 1:
CCCP, CCPC, CPCC, PCCC
{0, 1}
n = 2, k = 3:
000, 001, 010, 011, 100, 101, 110, 111
Неупорядоченные множества по k эл-ов, взятых из n данных и отличающиеся эл-ми.
Эл-ты могут повторяться до k раз (n≥1, k≥1)
{0, 1}
n = 2, k = 3:
000, 001, 011, 111
Слайд 9IV. Решение задач
Задача 1.
Десять участников полуфинала разыгрывают три путевки в
Дано:
n = 10
k = 3
Найти:
N = ?
Решение:
Ответ: 120
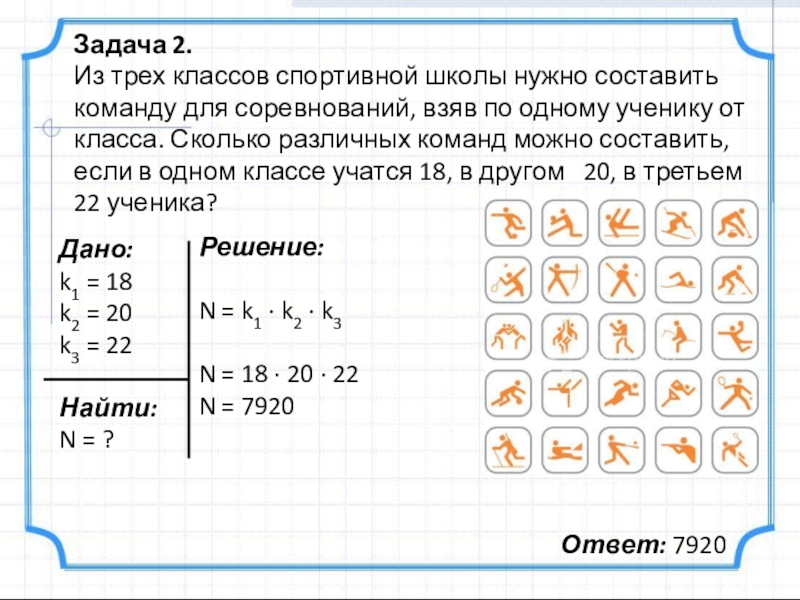
Слайд 10Задача 2.
Из трех классов спортивной школы нужно составить команду для
Дано:
k1 = 18
k2 = 20
k3 = 22
Найти:
N = ?
Решение:
N = k1 · k2 · k3
N = 18 · 20 · 22
N = 7920
Ответ: 7920
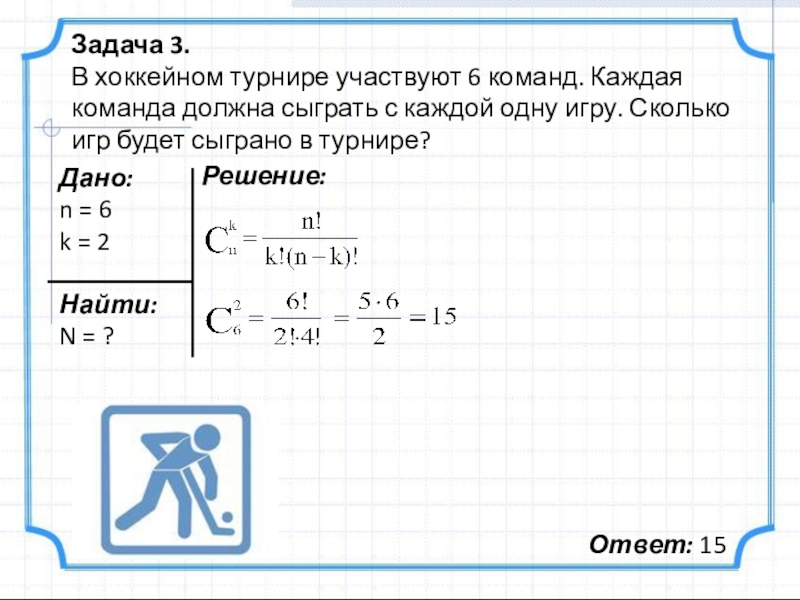
Слайд 11Задача 3.
В хоккейном турнире участвуют 6 команд. Каждая команда должна
Дано:
n = 6
k = 2
Найти:
N = ?
Решение:
Ответ: 15
Слайд 12Задача 4. Из 7 разноцветных карточек разрезной азбуки составлено слово колокол.
Дано:
nК = 2
nО = 3
nЛ = 2
Найти:
Nколокол = ?
Решение:
N = 2 · 3 · 2 · 2 · 1 · 1 · 1
N = 24
2
колокол
3
2
2
1
1
1
Ответ: 24
Слайд 13Задача 5.
Сколько экзаменационных комиссий, состоящих из 7 человек, можно создать из
Дано:
n = 14
k = 7
Найти:
N = ?
Решение:
Ответ: 3432
Слайд 14Задача 6.
В ящике находится 20 деталей. Известно, что 5 из
Дано:
n = 14
k = 7
Найти:
N = ?
Решение:
Метод 1
Способов выбрать 3 детали из 20
Способов выбрать 3 нестандартные детали
3 стандартных
Метод 2
2 стандартных
1 стандартная
Ответ: 685
Слайд 15Задача 7.
Собрание из 40 человек избирает председателя, секретаря и 5 членов
Сколько различных комиссий может быть составлено?
Дано:
n = 40
kп = 1
kс = 1
kк = 5
Найти:
N = ?
Решение:
Выбор председателя
Выбор секретаря
Выбор 5 членов комиссии
Ответ: 783029520
Слайд 16Задача 8.
Из 10 роз и 8 георгинов нужно составить букет,
Сколько можно составить различных букетов?
Дано:
n1 = 10
n2 = 8
k1 = 2
k2 = 3
Найти:
N = ?
Выбор 2 роз из 10
Выбор 3 георгинов из 8
Ответ: 2520
Слайд 17Задача 9.
Сколько существует различных семизначных телефонных номеров?
Дано:
n = 10
k
Найти:
N = ?
Решение:
Ответ: 10000000
Слайд 18Задача 10.
Сколько существует различных семизначных телефонных номеров, если в каждом номере
Дано:
n = 10
k = 7
Найти:
N = ?
Решение:
Ответ: 604800
Слайд 19Задача 11.
Имеется 9 различных книг, четыре из которых- учебники . Сколькими
1) Рассмотрим учебники как одну книгу
⇒
Способов расставить 6 книг: P6 = 6!
2) В каждой комбинации перестановок учебников: P4 = 4!
3) Число способов расположения книг:
N = Р6 · Р4=6! · 4!=720 · 24 = 17280
Дано:
n = 9
kу = 4
Найти:
N = ?
Решение:
Ответ: 17280
Слайд 20
Задача 12.
Сколько нужно взять элементов, чтобы число размещений из них по
Решение:
∉ОО
Ответ: 6
Слайд 21Задача 13.
Сколькими способами можно расположить в ряд две зеленые и четыре
Дано:
n = 6
k1 = 2
k2 = 4
Найти:
N = ?
Решение:
Ответ: 15
Слайд 22Задача 14.
Сколькими способами можно переставить буквы в слове «математика», чтобы получались
Дано:
n = 10
U = {М, А, Т, Е, И, К}
Найти:
N = ?
Ответ: 151200
Решение:
Слайд 23Задача 15.
В кондитерской имеется 5 разных сортов пирожных. Сколькими способами можно
Дано:
n = 5
k = 4
Найти:
N = ?
Ответ: 70
Решение:




















![Презентация по теме Комбинаторика Домашнее задание*1_Комбинаторика [ДЗ].docДЗ Домашнее задание*1_Комбинаторика [ДЗ].docДЗ](/img/thumbs/daa4b5fd1ccef877c7beaf5438d5f0a8-800x.jpg)