- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задачи на построение
Содержание
- 1. Презентация по математике Задачи на построение
- 2. В геометрии выделяют задачи на построение, которые
- 3. АВСДано: угол А.ОDEТеперь докажем, что построенный угол равен данному.Построить угол, равный данному.*ГБОУ ЦО №633
- 4. Дано: угол А.АПостроили угол О.ВСОDEДоказать:
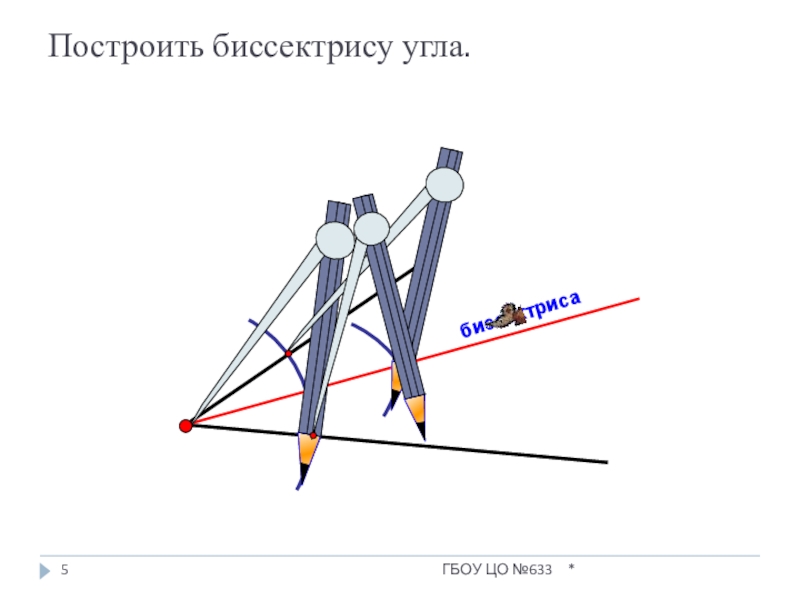
- 5. биссектрисаПостроить биссектрису угла.*ГБОУ ЦО №633
- 6. Докажем, что луч АВ – биссектриса
- 7. Построить квадрат, зная длину его диагонали.Строим произвольный
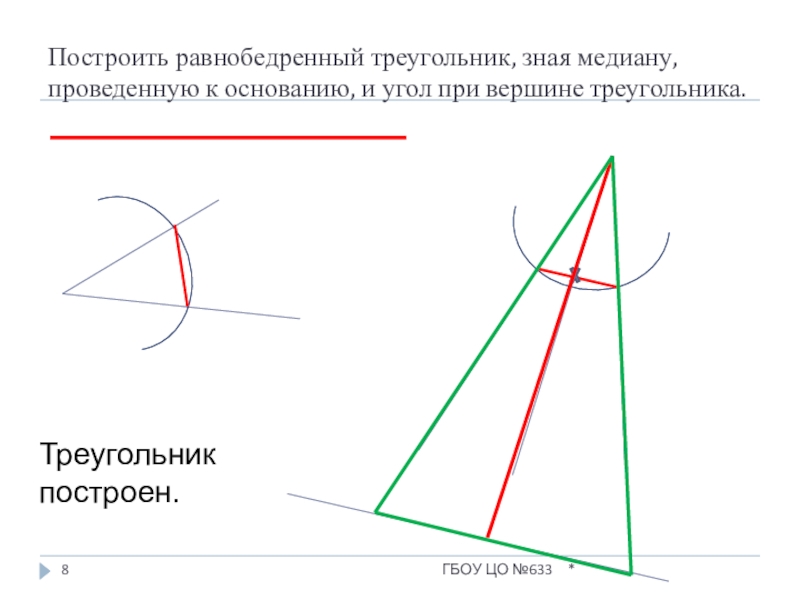
- 8. Построить равнобедренный треугольник, зная медиану, проведенную к основанию, и угол при вершине треугольника.Треугольник построен.*ГБОУ ЦО №633
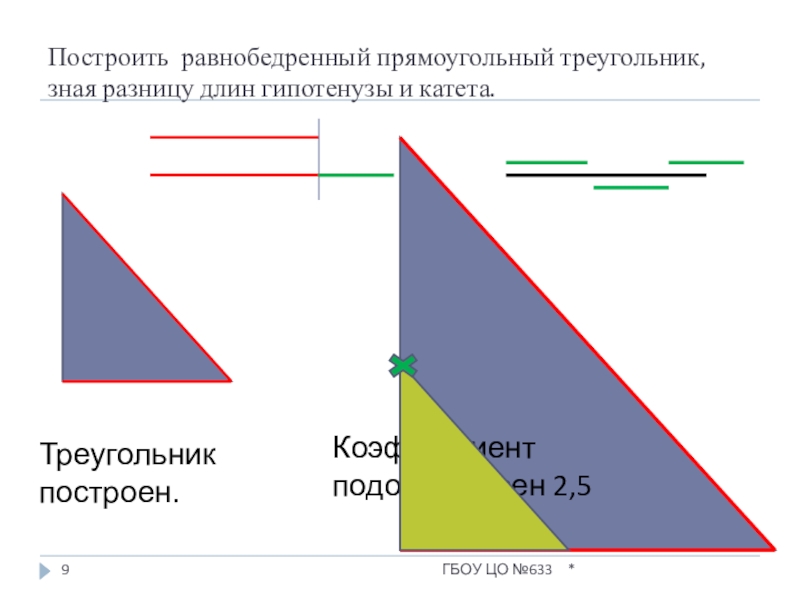
- 9. Построить равнобедренный прямоугольный треугольник, зная разницу длин гипотенузы и катета.Коэффициент подобия равен 2,5Треугольник построен.*ГБОУ ЦО №633
- 10. 1. Постройте квадрат, зная разность между длиной
- 11. Постройте окружность, зная длины двух хорд, проведенных
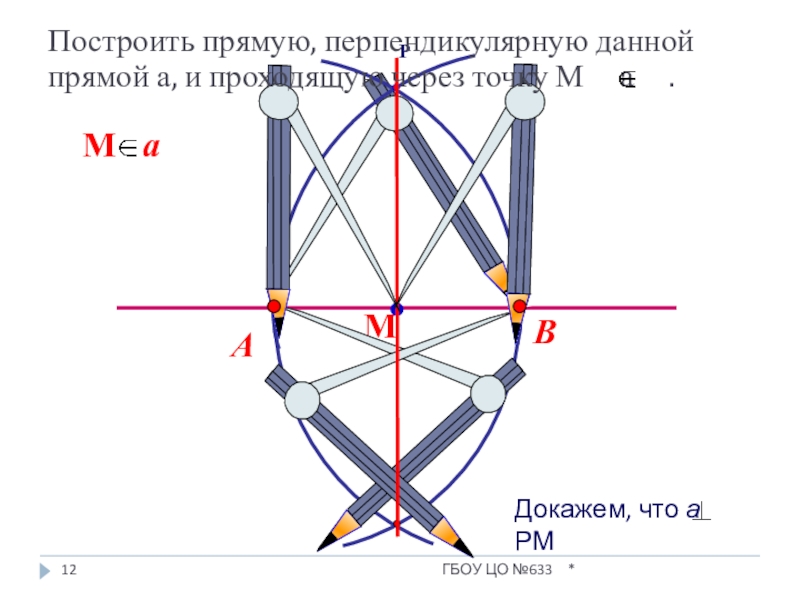
- 12. ВАПостроить прямую, перпендикулярную данной прямой а, и
- 13. Докажем, что а РМАМ=МВ, как радиусы
- 14. aNМПостроить прямую, перпендикулярную данной прямой а, которая
- 15. aNBACМПосмотрим на расположение циркулей.АМ=АN=MB=BN, как равные радиусы.
- 16. Задачи на построениеСпасибо за работу!
Слайд 2В геометрии выделяют задачи на построение, которые можно решить только с
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
*
ГБОУ ЦО №633
Слайд 3А
В
С
Дано: угол А.
О
D
E
Теперь докажем, что построенный угол равен данному.
Построить угол, равный
*
ГБОУ ЦО №633
Слайд 4
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А = О
Доказательство:
АС=ОЕ, как радиусы одной окружности.
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Построить угол, равный данному.
*
ГБОУ ЦО №633
Слайд 6
Докажем, что луч АВ – биссектриса А
Дополнительное построение.
Докажем равенство
треугольников ∆ АСВ и ∆ АDB.
3. Выводы
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
*
ГБОУ ЦО №633
Слайд 7Построить квадрат, зная длину его диагонали.
Строим произвольный квадрат. Измеряем длину его
Квадрат по заданной длине диагонали построен.
*
ГБОУ ЦО №633
Слайд 8Построить равнобедренный треугольник, зная медиану, проведенную к основанию, и угол при
Треугольник построен.
*
ГБОУ ЦО №633
Слайд 9Построить равнобедренный прямоугольный треугольник, зная разницу длин гипотенузы и катета.
Коэффициент подобия
Треугольник построен.
*
ГБОУ ЦО №633
Слайд 101. Постройте квадрат, зная разность между длиной диагонали и стороны квадрата. 2.
*
ГБОУ ЦО №633
Слайд 11Постройте окружность, зная длины двух хорд, проведенных из одной точки этой
1. Строим угол, равный данному.
2. Осталось построить окружность, описанную вокруг полученного треугольника.
*
ГБОУ ЦО №633
Слайд 12
В
А
Построить прямую, перпендикулярную данной прямой а, и проходящую через точку М
*
ГБОУ ЦО №633
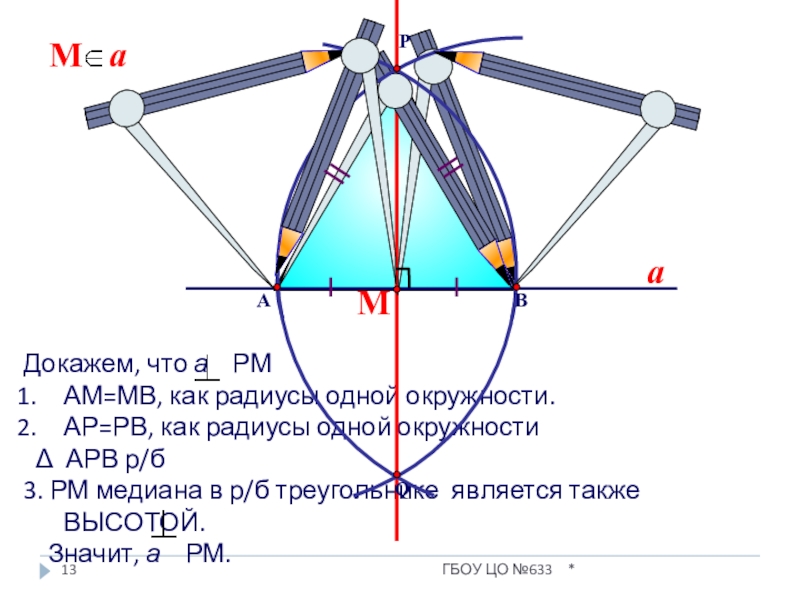
Слайд 13Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как радиусы
Δ АРВ р/б
3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.
Значит, а РМ.
М
a
*
ГБОУ ЦО №633
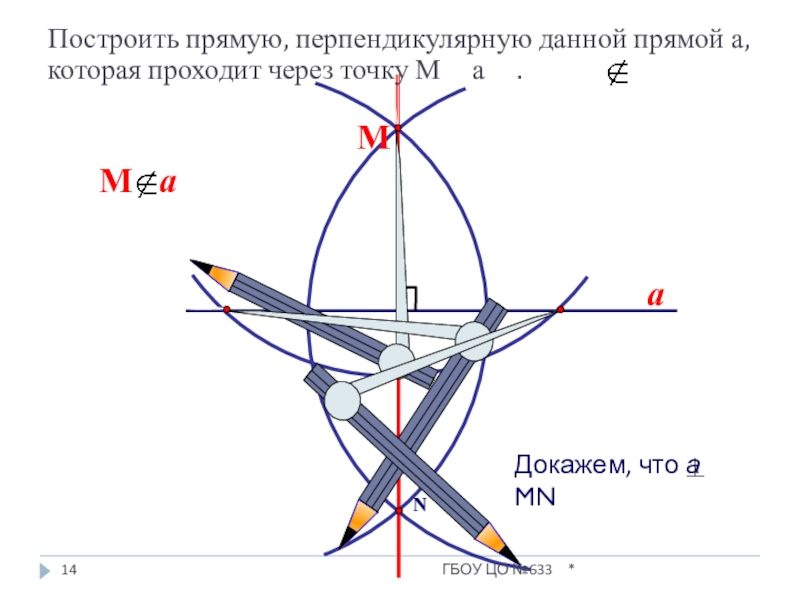
Слайд 14
a
N
М
Построить прямую, перпендикулярную данной прямой а, которая проходит через точку М
*
ГБОУ ЦО №633
Слайд 15
a
N
B
A
C
М
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN=
по трем сторонам
*
ГБОУ ЦО №633