- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике тема
Содержание
- 1. Презентация по математике тема
- 2. 1- как получается эта фигура? 2- как
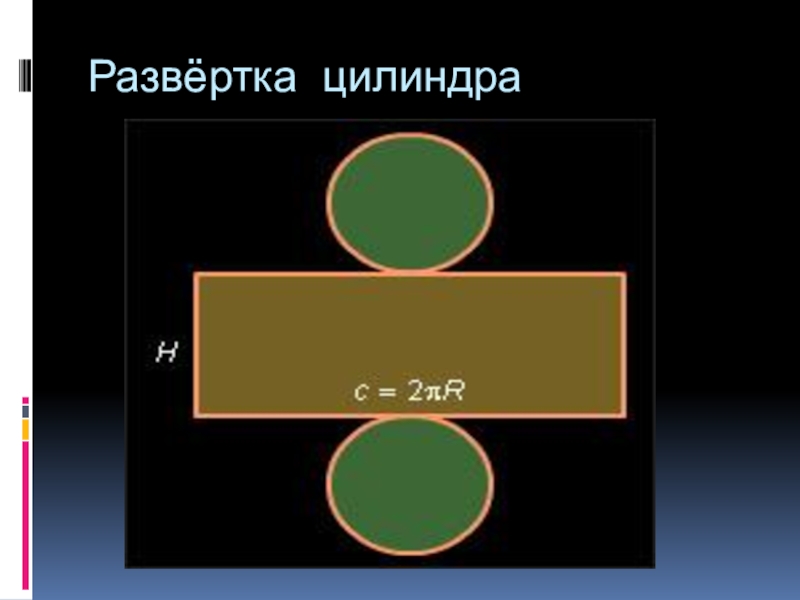
- 3. Развёртка цилиндра
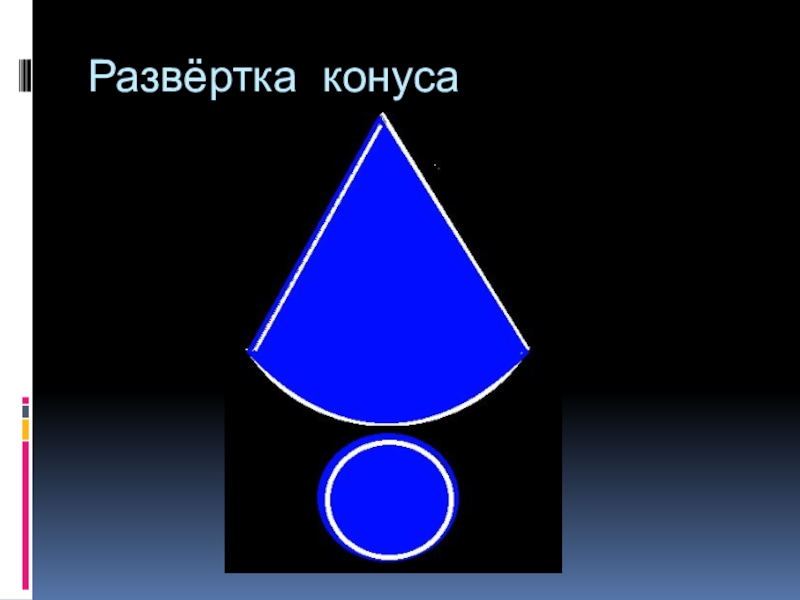
- 4. Развёртка конуса
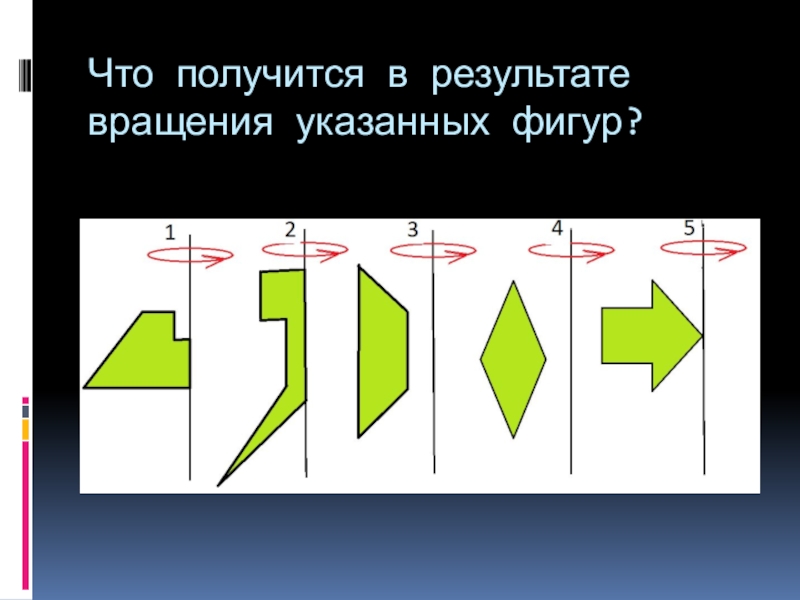
- 5. Что получится в результате вращения указанных фигур?
- 6. Тест 1(выбрать правильные ответы)Основания цилиндра равны.Высота конуса
- 7. Тест 2(выбрать правильные ответы)1. Боковой поверхностью пирамиды
- 8. Тест 3(заполнить пропуски)1. Если основание призмы есть
- 9. Тест 4(заполнить пропуски)Всякое сечение шара плоскостью есть
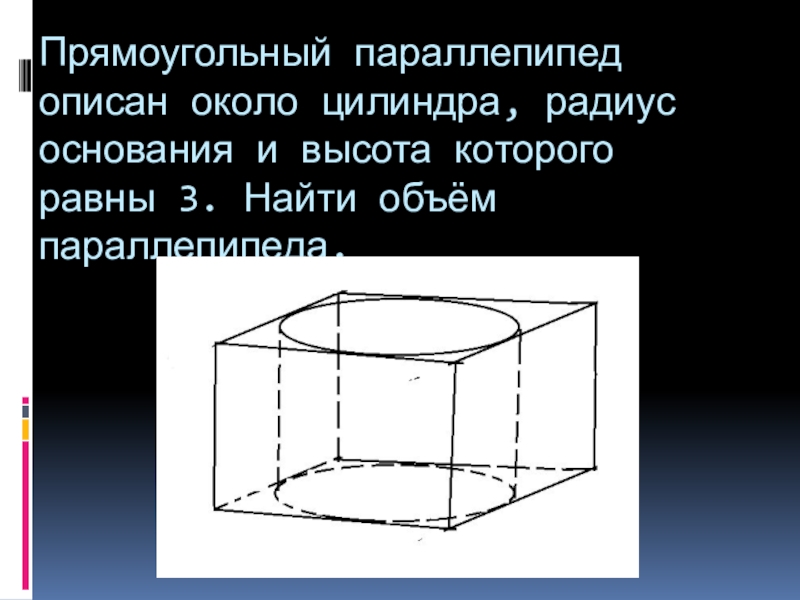
- 10. Прямоугольный параллепипед описан около цилиндра, радиус основания и высота которого равны 3. Найти объём параллепипеда.
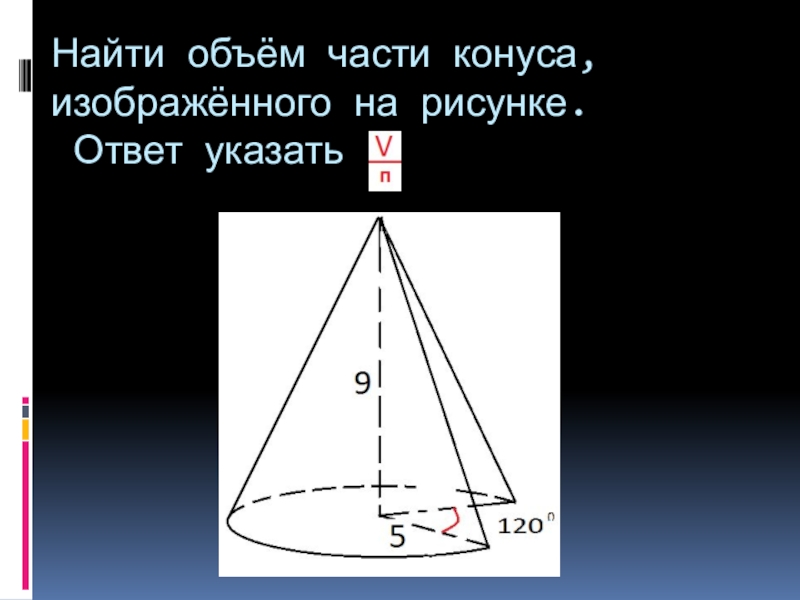
- 11. Найти объём части конуса, изображённого на рисунке. Ответ указать
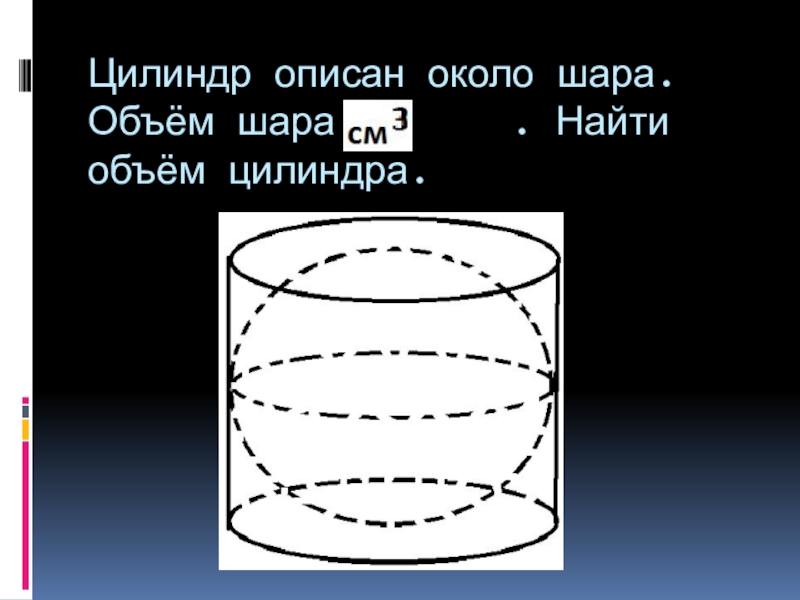
- 12. Цилиндр описан около шара. Объём шара 8 . Найти объём цилиндра.
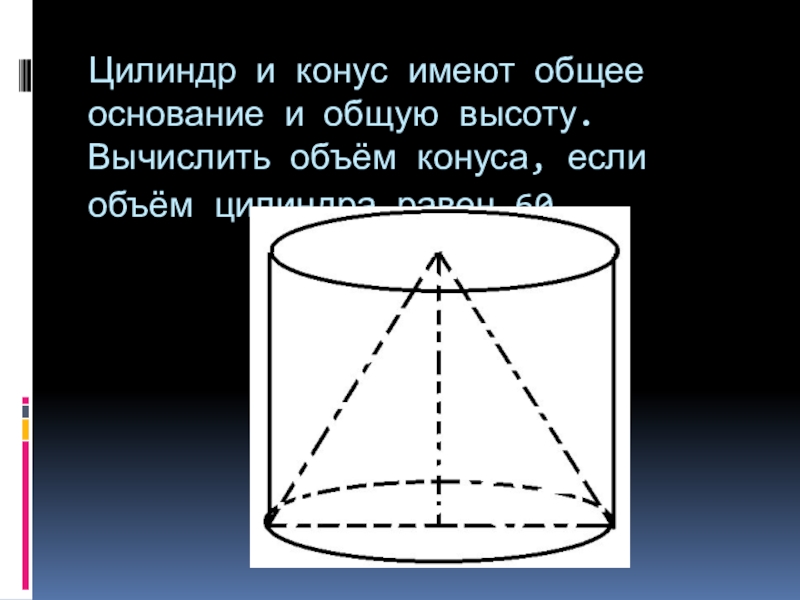
- 13. Цилиндр и конус имеют общее основание и
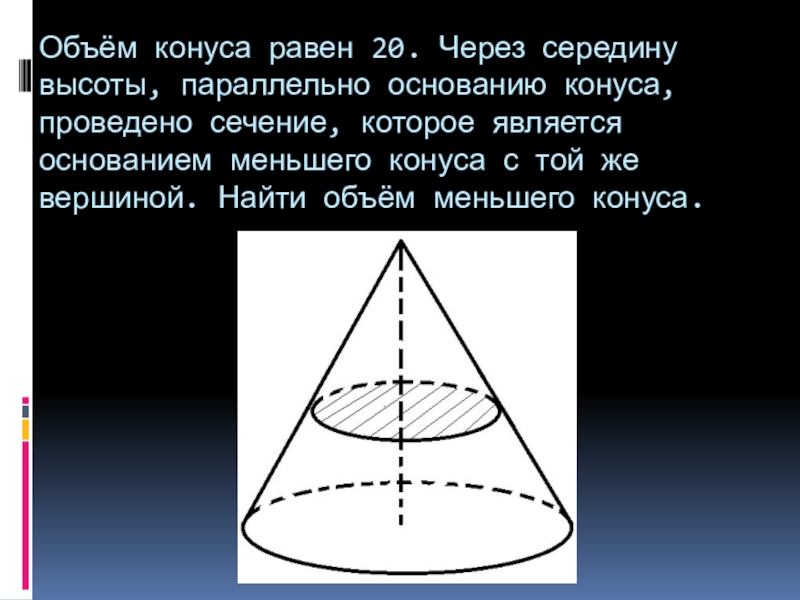
- 14. Объём конуса равен 20. Через середину высоты,
- 15. Цилиндр
- 16. Слайд 16
- 17. Шар: историяОба слова "шар" и "сфера" происходят
- 18. Шары из жизни
- 19. Гигантский шар в игрушечном городеЭто - космический
- 20. Гиперболоид вращенияШуховская радиобашняБашня для радиостанции в
- 21. Тор – фигура вращенияТор образуется при вращении
- 22. Объем и площадь поверхности тораЕсли r –
- 23. Слайд 23
- 24. Гироскоп
- 25. Купола
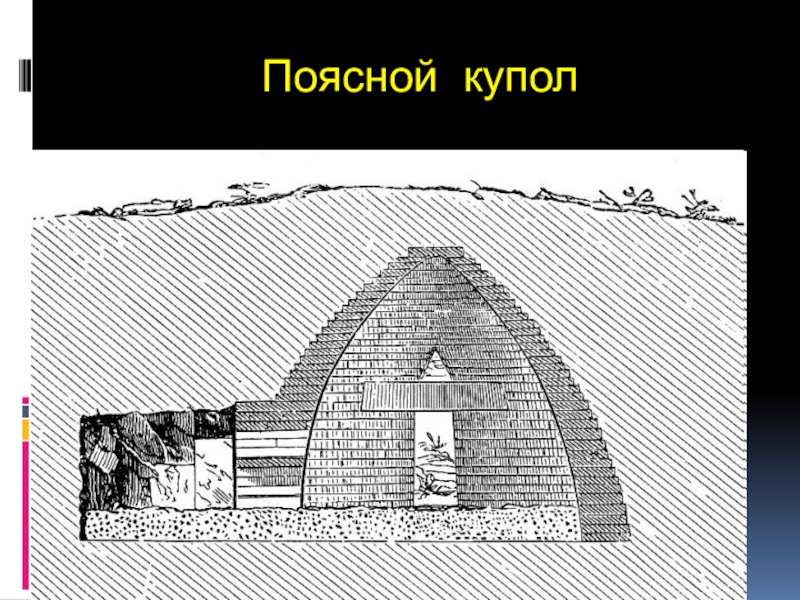
- 26. Поясной купол
- 27. Купол- зонтик
- 28. Овальный купол
- 29. Купол-блюдце
- 30. Купол-луковица
- 31. Купол-луковица
- 32. Слайд 32
- 33. . Знания о телах вращения необходимы не только
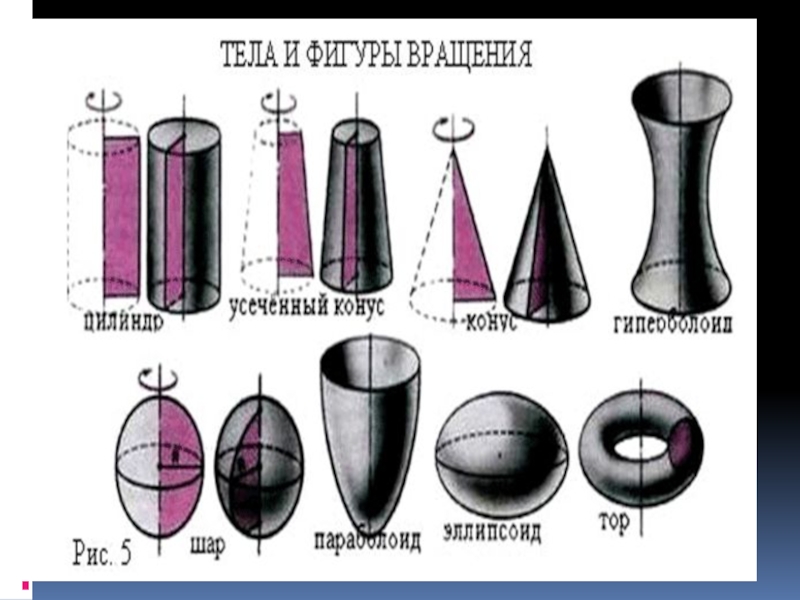
1- как получается эта фигура? 2- как она называется? 3- назовите элементы этой фигуры 4- что представляет из себя развёртка боковой поверхности? 5- чему равна площадь полной поверхности фигуры? 6- чему равен объём фигуры? 7- назовите
Слайд 21- как получается эта фигура? 2- как она называется? 3- назовите элементы этой
фигуры
4- что представляет из себя развёртка боковой поверхности?
5- чему равна площадь полной поверхности фигуры?
6- чему равен объём фигуры?
7- назовите предметы, имеющие форму этой фигуры
Слайд 6Тест 1
(выбрать правильные ответы)
Основания цилиндра равны.
Высота конуса – это прямая.
Концы любого
диаметра называются диаметрально противоположными точками шара.
Через любую точку шаровой поверхности проходит единственная касательная прямая
Через любую точку шаровой поверхности проходит единственная касательная прямая
Слайд 7Тест 2
(выбрать правильные ответы)
1. Боковой поверхностью пирамиды называется сумма площадей всех
ее граней.
2. Боковая поверхность равна Р х Н.
3. Основания усеченной пирамиды равны.
4. Все грани параллелепипеда параллелограммы.
5. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
2. Боковая поверхность равна Р х Н.
3. Основания усеченной пирамиды равны.
4. Все грани параллелепипеда параллелограммы.
5. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Слайд 8Тест 3
(заполнить пропуски)
1. Если основание призмы есть _______________ , то она
называется параллелепипедом.
2. Часть пирамиды, заключенная между основанием и плоскостью, параллельной основанию, называется ______________ .
3. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется ____________ .
4. Призма называется ___________ , если ее боковые ребра перпендикулярны основаниям.
2. Часть пирамиды, заключенная между основанием и плоскостью, параллельной основанию, называется ______________ .
3. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется ____________ .
4. Призма называется ___________ , если ее боковые ребра перпендикулярны основаниям.
Слайд 9Тест 4
(заполнить пропуски)
Всякое сечение шара плоскостью есть ___________ .
Тело, полученное при
вращении _______________ вокруг оси, совпадающей с диаметром, называется шаром.
Тело, полученное при вращении прямоугольного треугольника вокруг оси, совпадающей с одним из его катетов, называется ____________ .
Осевые сечения усеченного конуса называются ___________ .
Тело, полученное при вращении прямоугольного треугольника вокруг оси, совпадающей с одним из его катетов, называется ____________ .
Осевые сечения усеченного конуса называются ___________ .
Слайд 10Прямоугольный параллепипед описан около цилиндра, радиус основания и высота которого равны
3. Найти объём параллепипеда.
Слайд 13Цилиндр и конус имеют общее основание и общую высоту. Вычислить объём
конуса, если объём цилиндра равен 60.
Слайд 14Объём конуса равен 20. Через середину высоты, параллельно основанию конуса, проведено
сечение, которое является основанием меньшего конуса с той же вершиной. Найти объём меньшего конуса.
Слайд 17Шар: история
Оба слова "шар" и "сфера" происходят от одного и того
же греческого слова "сфайра" - мяч. При этом слово "шар" образовалось от перехода согласных сф в ш. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы.
Слайд 19Гигантский шар в игрушечном городе
Это - космический корабль "Земля", рсположенный на
окраине ДИСНЕЙЛЕНДА в штате Флорида. По задумке эта сферическая конструкция должна оли- цетворять будущее человечества.
Слайд 20
Гиперболоид вращения
Шуховская радиобашня
Башня для радиостанции в Москве на Шаболовке, построенная
по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей - гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности.
Слайд 21Тор – фигура вращения
Тор образуется при вращении окружности вокруг не пересекающей
её прямой, лежащей в плоскости окружности.
Если «заполнить» тор, то получится тело вращения, называемое полноторием.
Если «заполнить» тор, то получится тело вращения, называемое полноторием.
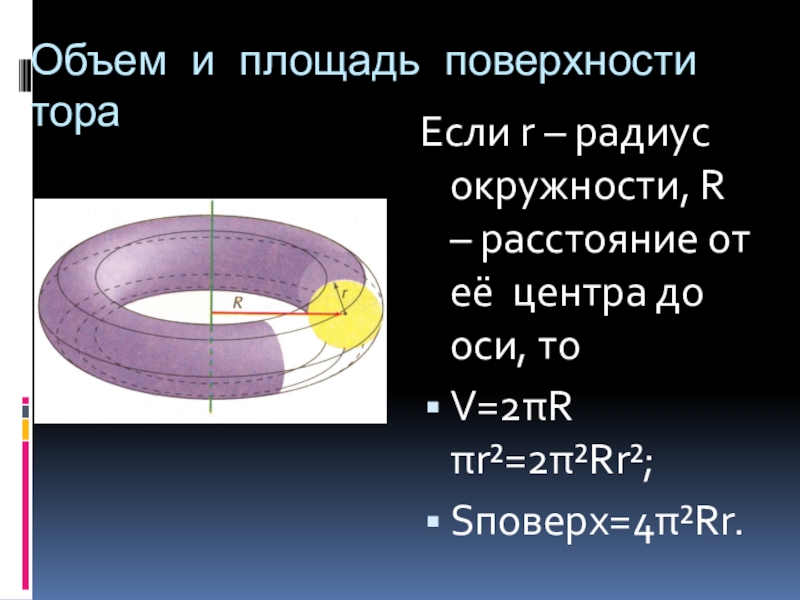
Слайд 22Объем и площадь поверхности тора
Если r – радиус окружности, R –
расстояние от её центра до оси, то
V=2πR πr²=2π²Rr²;
Sповерх=4π²Rr.
V=2πR πr²=2π²Rr²;
Sповерх=4π²Rr.
Слайд 33. Знания о телах вращения необходимы не только в астрономии, но и
в технике, строительстве жилых домов, дворцов, храмов, куполов, в воздухоплавании на воздушных шарах и во многом другом. Они помогают познать красоту мира.