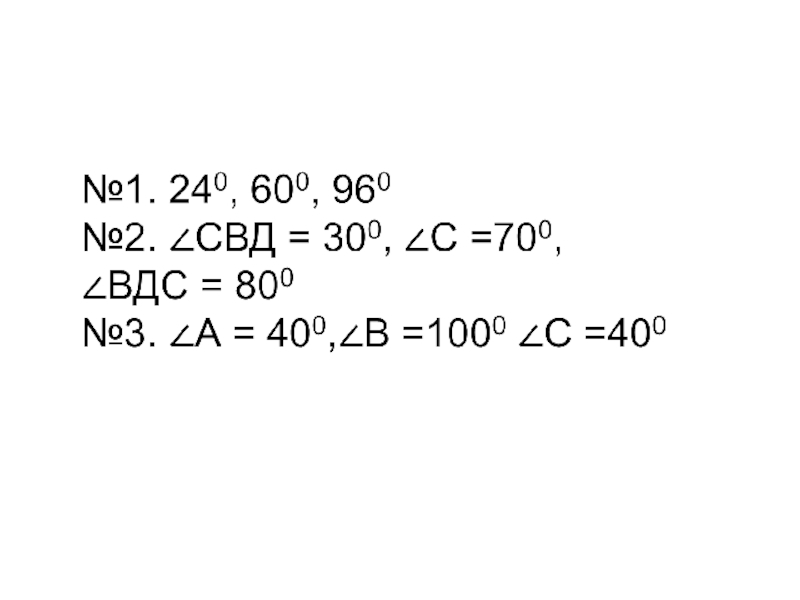- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуСумма углов треугольника
Содержание
- 1. Презентация по математике на темуСумма углов треугольника
- 2. … Да, путь познания не гладок. Но
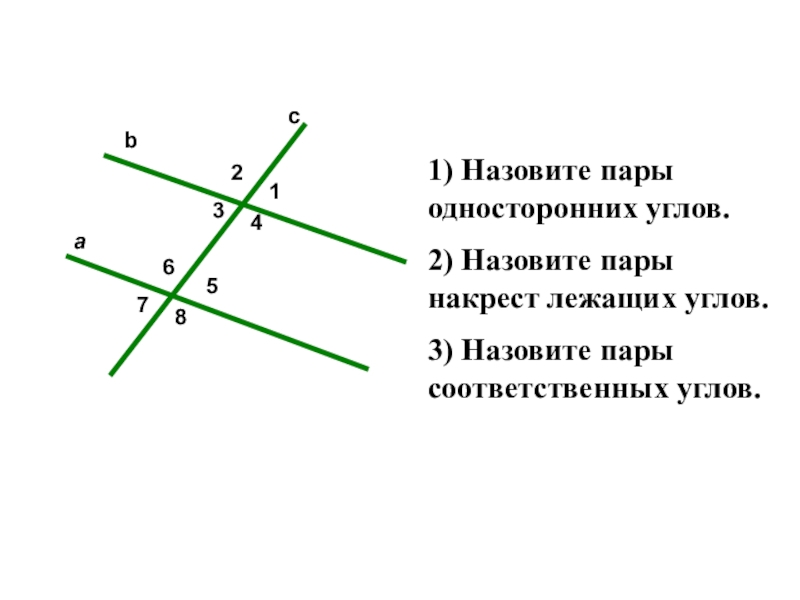
- 3. 25687143acb1) Назовите пары односторонних углов.2) Назовите пары накрест лежащих углов.3) Назовите пары соответственных углов.
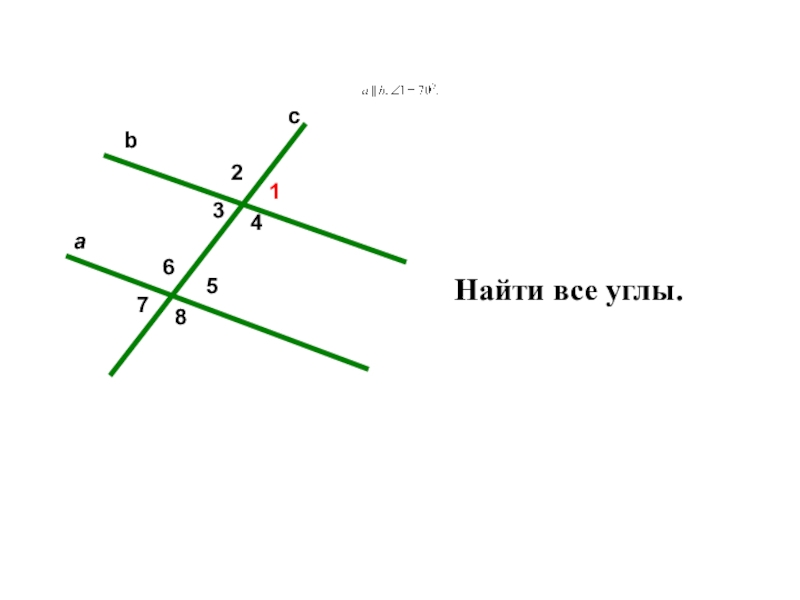
- 4. 25687143acbНайти все углы.
- 5. Дано: ∆ АВС;
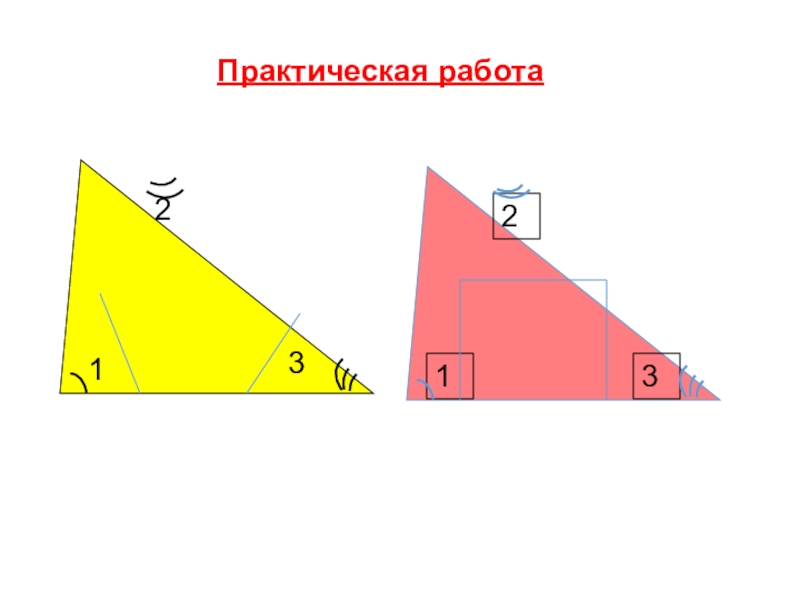
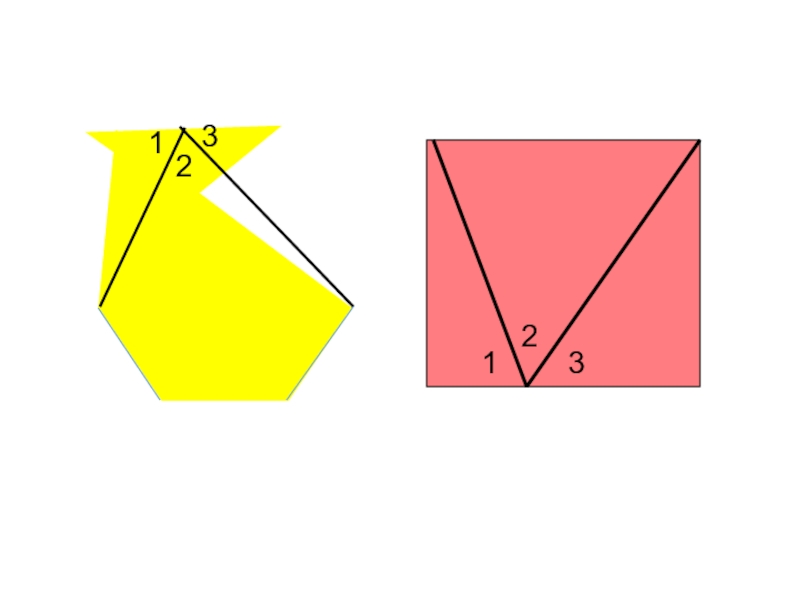
- 6. Практическая работа
- 7. 321
- 8. Сумма углов треугольникаКлассная работа
- 9. Цели обущения: 7.3.2.13 доказывать теорему о сумме
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Первое доказательство было дано еще Пифагором (5
- 15. А B C 1 2 3 4
- 16. Домашняя работа:3 способ доказательства:Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.
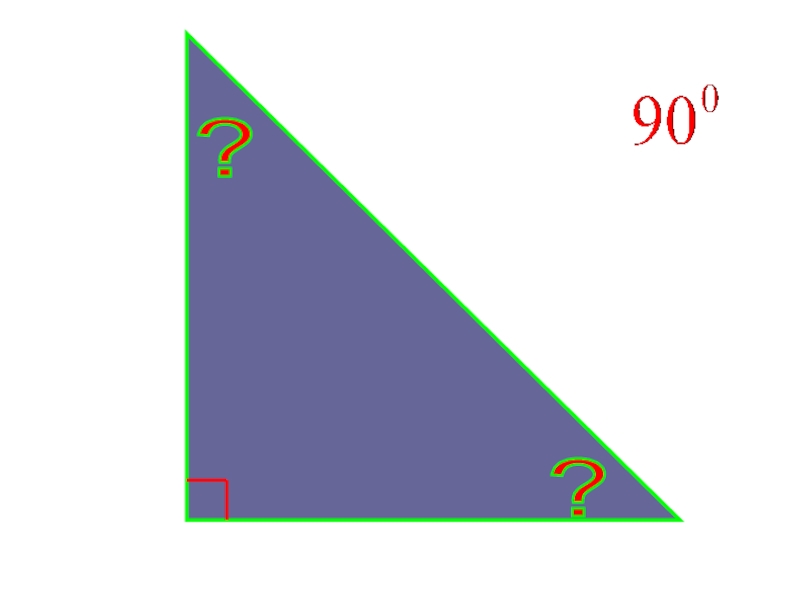
- 17. ? ? ?
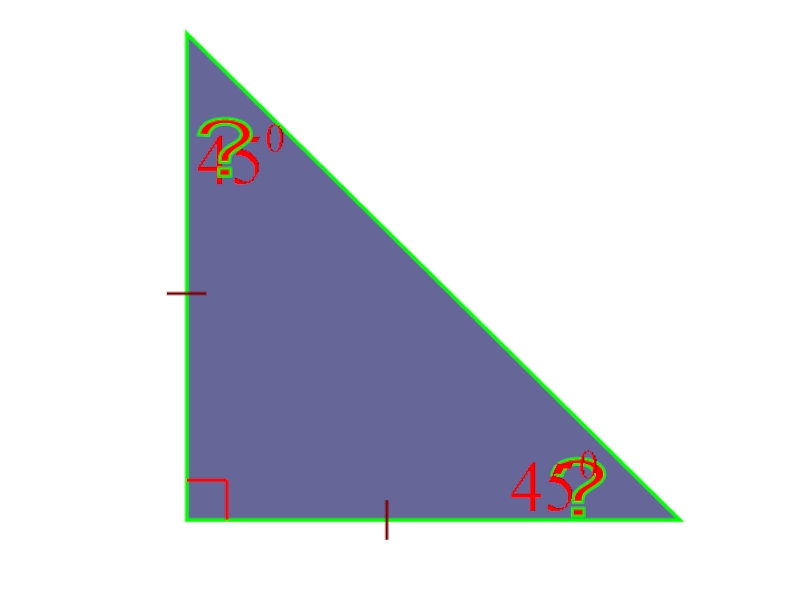
- 18. ? ?
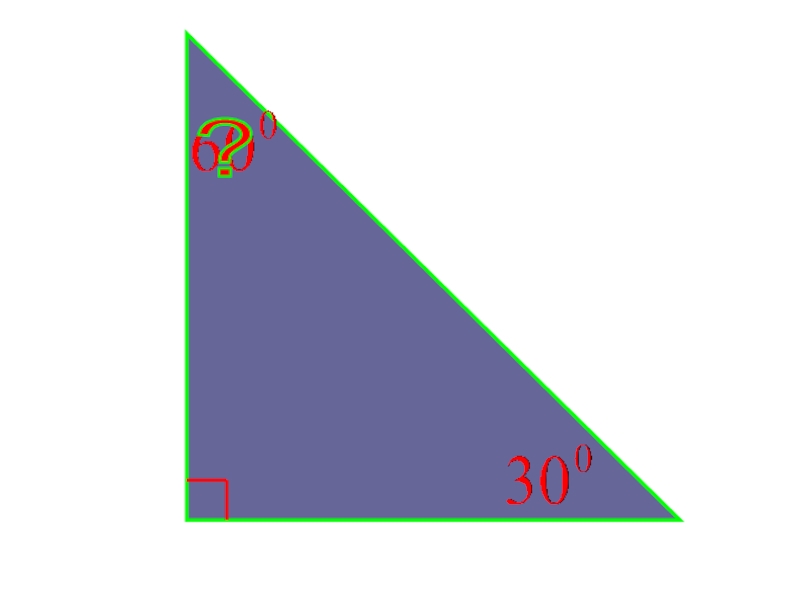
- 19. ? ?
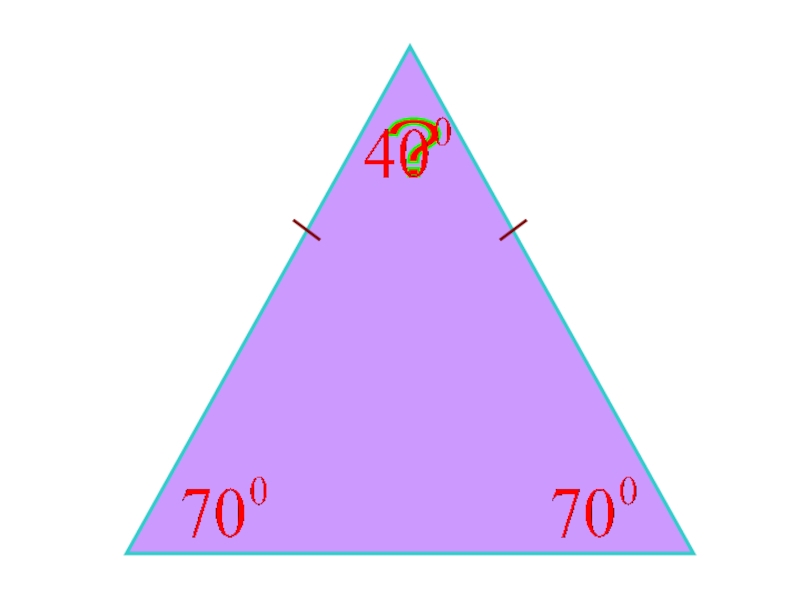
- 20. ?
- 21. ?
- 22. ? ?
- 23. Разминка для глаз
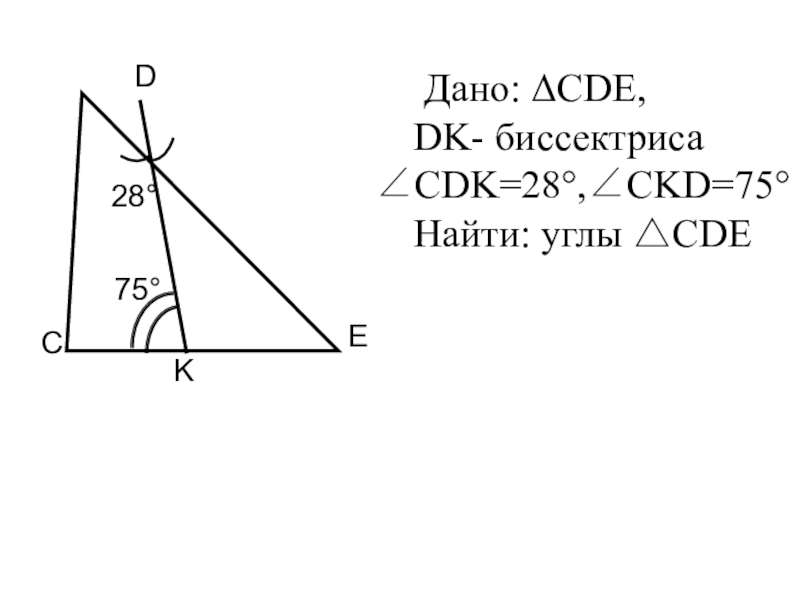
- 24. Дано: ΔCDE, DK- биссектриса ∠CDK=28°,∠CKD=75°Найти: углы △CDE
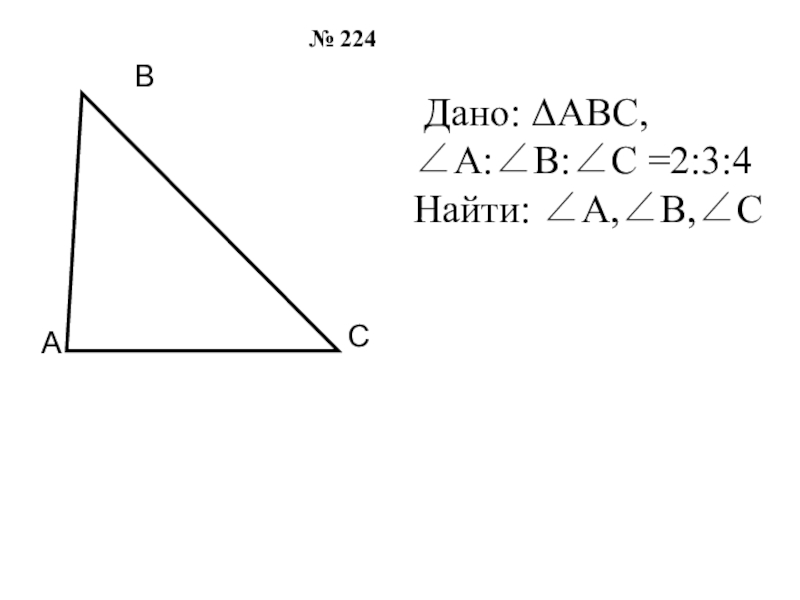
- 25. Дано: ΔАВС, ∠А:∠В:∠С =2:3:4Найти: ∠А,∠В,∠С № 224
- 26. Ответы к тесту - достижений: Вариант 11800 да3001200 700 Вариант 21800 нет800600 400
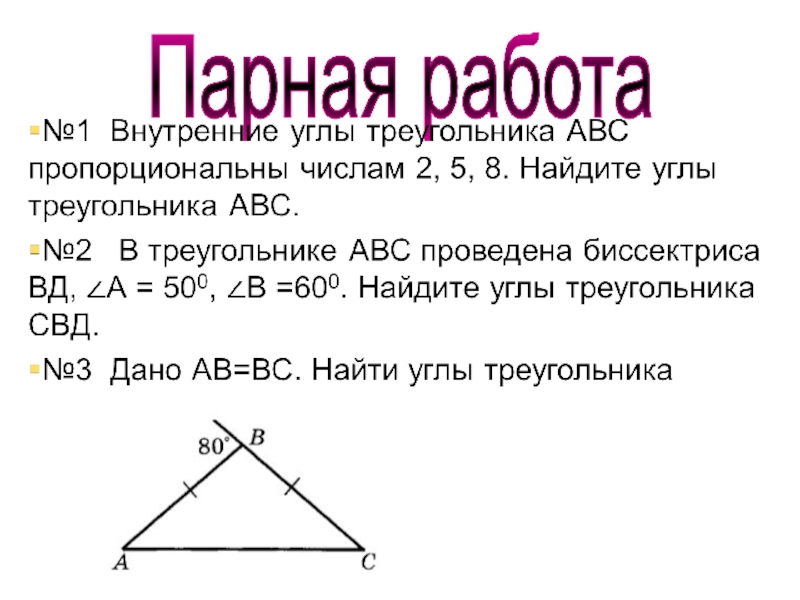
- 27. Парная работа
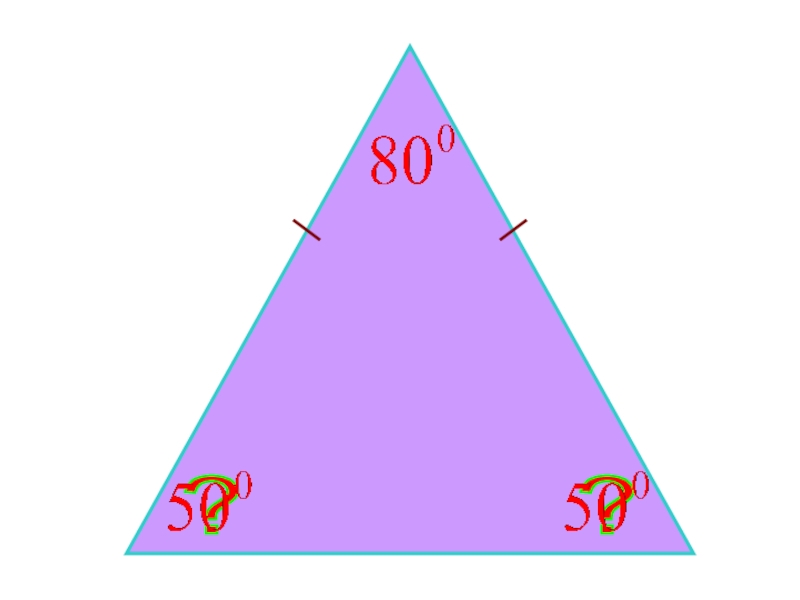
- 28.
- 29. Рефлексия
… Да, путь познания не гладок. Но знаем мы со школьных лет, Загадок больше, чем разгадок, И поиска предела нет.
Слайд 2… Да, путь познания не гладок. Но знаем мы со школьных лет, Загадок
больше, чем разгадок,
И поиска предела нет.
Пифагор.
Слайд 32
5
6
8
7
1
4
3
a
c
b
1) Назовите пары односторонних углов.
2) Назовите пары накрест лежащих углов.
3) Назовите
пары соответственных углов.
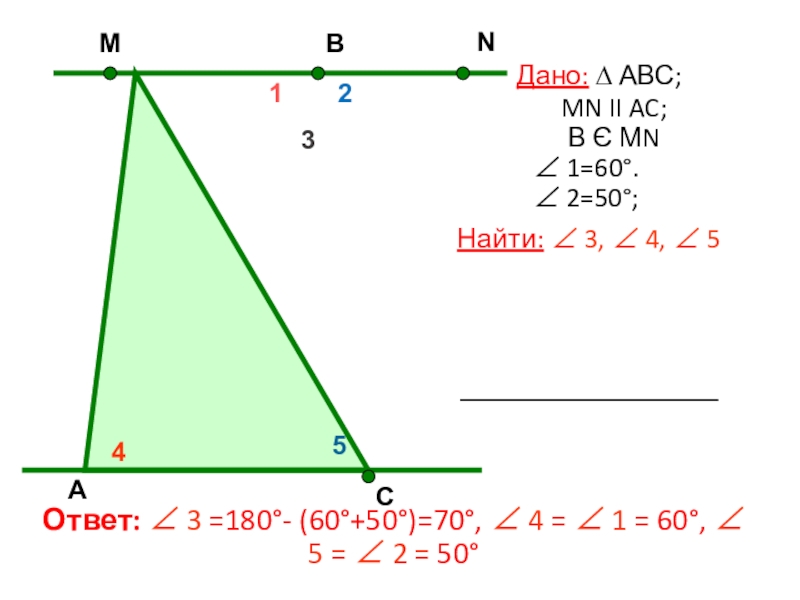
Слайд 5 Дано: ∆ АВС; MN II
AC;
В Є МN
∠ 1=60°.
∠ 2=50°;
Найти: ∠ 3, ∠ 4, ∠ 5
Ответ: ∠ 3 =180°- (60°+50°)=70°, ∠ 4 = ∠ 1 = 60°, ∠ 5 = ∠ 2 = 50°
А
N
С
В
М
4
2
1
5
3
Слайд 9Цели обущения:
7.3.2.13 доказывать теорему о сумме углов треугольника и следствия
из нее;
7.3.3.7 решать задачи на вычисление и доказательство, применяя теорему о сумме углов треугольника и следствия из нее;
7.3.2.14 уметь выводить признак равенства прямоугольных треугольников на основе теоремы о сумме углов треугольника;
7.3.3.7 решать задачи на вычисление и доказательство, применяя теорему о сумме углов треугольника и следствия из нее;
7.3.2.14 уметь выводить признак равенства прямоугольных треугольников на основе теоремы о сумме углов треугольника;
Слайд 12
Дано: ∆ АВС
Доказать:
∠ А +∠ В+∠ С =180°
Доказательство:
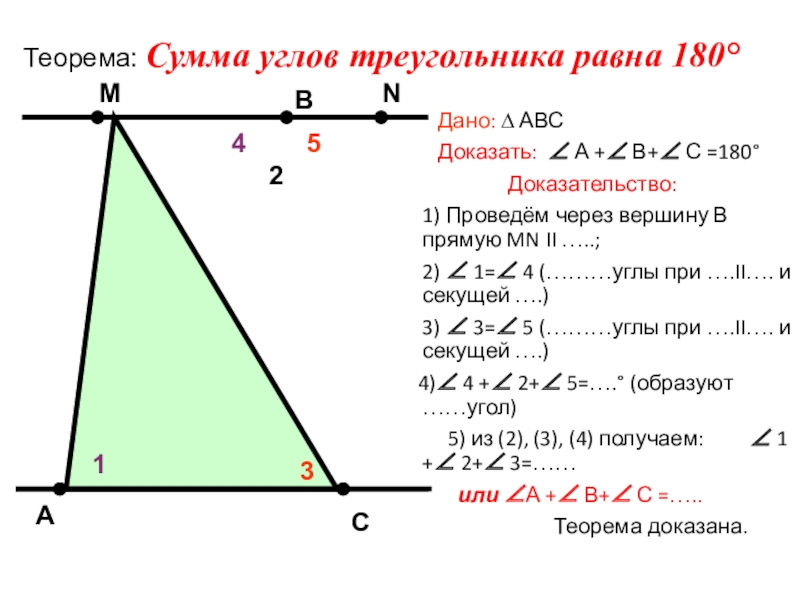
1) Проведём через вершину В прямую MN II …..;
2) ∠ 1=∠ 4 (………углы при ….II…. и секущей ….)
3) ∠ 3=∠ 5 (………углы при ….II…. и секущей ….)
4)∠ 4 +∠ 2+∠ 5=….° (образуют ……угол)
5) из (2), (3), (4) получаем: ∠ 1 +∠ 2+∠ 3=……
или ∠А +∠ В+∠ С =…..
Теорема доказана.
Доказательство:
1) Проведём через вершину В прямую MN II …..;
2) ∠ 1=∠ 4 (………углы при ….II…. и секущей ….)
3) ∠ 3=∠ 5 (………углы при ….II…. и секущей ….)
4)∠ 4 +∠ 2+∠ 5=….° (образуют ……угол)
5) из (2), (3), (4) получаем: ∠ 1 +∠ 2+∠ 3=……
или ∠А +∠ В+∠ С =…..
Теорема доказана.
А
N
С
В
М
1
3
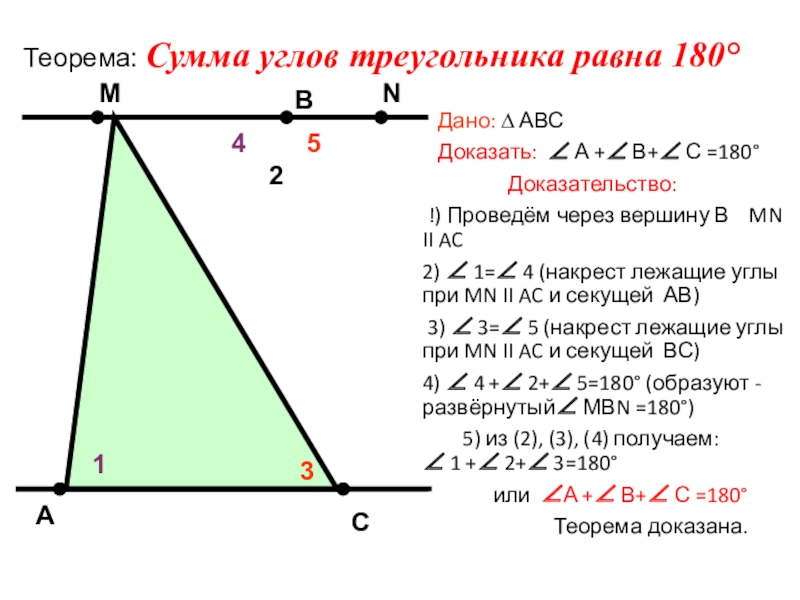
Теорема: Сумма углов треугольника равна 180°
2
4
5
Слайд 13
Дано: ∆ АВС
Доказать:
∠ А +∠ В+∠ С =180°
Доказательство:
!) Проведём через вершину В MN II AC
2) ∠ 1=∠ 4 (накрест лежащие углы при MN II AC и секущей АВ)
3) ∠ 3=∠ 5 (накрест лежащие углы при MN II AC и секущей ВС)
4) ∠ 4 +∠ 2+∠ 5=180° (образуют - развёрнутый∠ МВN =180°)
5) из (2), (3), (4) получаем: ∠ 1 +∠ 2+∠ 3=180°
или ∠А +∠ В+∠ С =180°
Теорема доказана.
Доказательство:
!) Проведём через вершину В MN II AC
2) ∠ 1=∠ 4 (накрест лежащие углы при MN II AC и секущей АВ)
3) ∠ 3=∠ 5 (накрест лежащие углы при MN II AC и секущей ВС)
4) ∠ 4 +∠ 2+∠ 5=180° (образуют - развёрнутый∠ МВN =180°)
5) из (2), (3), (4) получаем: ∠ 1 +∠ 2+∠ 3=180°
или ∠А +∠ В+∠ С =180°
Теорема доказана.
А
N
С
В
М
1
3
Теорема: Сумма углов треугольника равна 180°
2
4
5
Слайд 14Первое доказательство было дано еще Пифагором (5 в. до н.э.)
В первой
книге «Начала» Евклид излагает другое доказательство теоремы о сумме углов треугольника.
Слайд 15
А
B
C
1
2
3
4
D
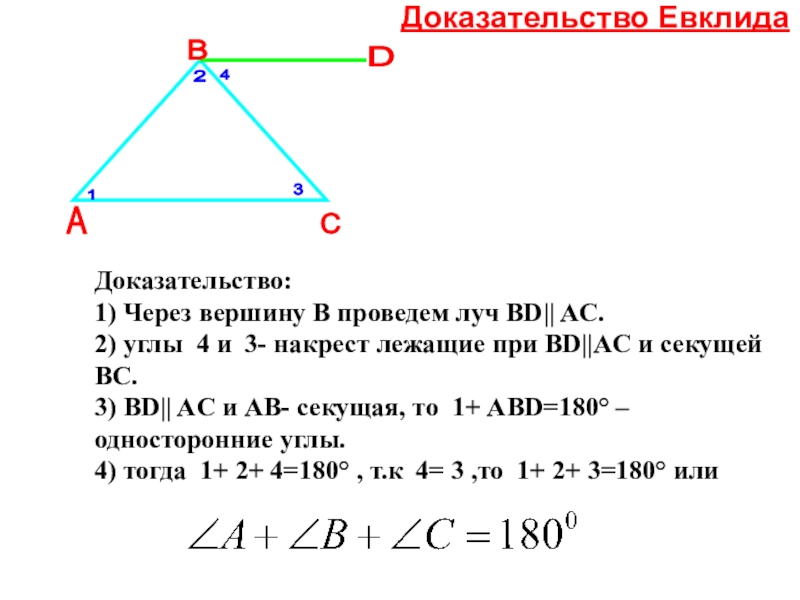
Доказательство:
1) Через вершину
B проведем луч BD|| AC.
2) углы 4 и 3- накрест лежащие при BD||AC и секущей BC.
3) BD|| AC и AB- секущая, то 1+ ABD=180° – односторонние углы.
4) тогда 1+ 2+ 4=180° , т.к 4= 3 ,то 1+ 2+ 3=180° или
Доказательство Евклида
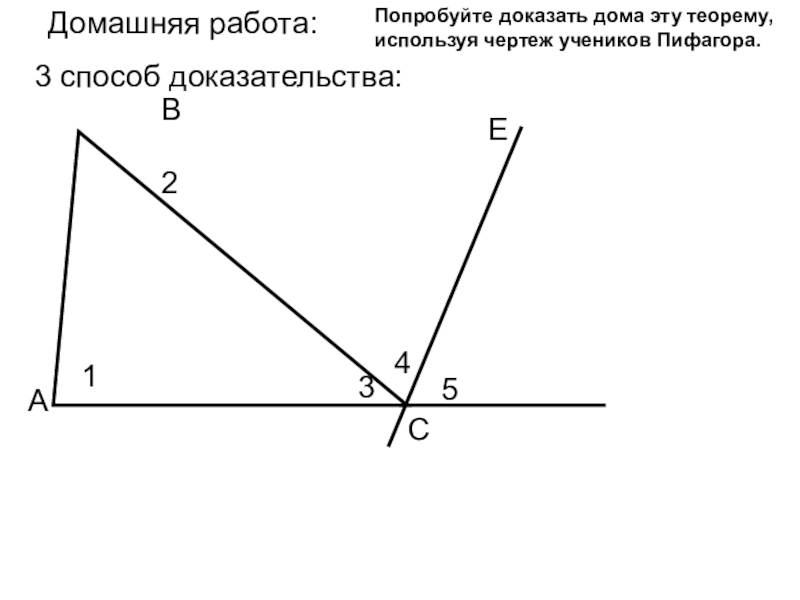
Слайд 16Домашняя работа:
3 способ доказательства:
Попробуйте доказать дома эту теорему, используя чертеж учеников
Пифагора.