- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи на четность (5-7 классы)
Содержание
- 1. Презентация по математике на тему Задачи на четность (5-7 классы)
- 2. К задачам на четность относятся: задачи на чередованиезадачи на разбиение на парызадачи на четность и нечетность
- 3. Задачи на чередование Свойства: Если в некоторой
- 4. Задача 116 корзин расположили по кругу. Можно
- 5. Решение: Пусть в 1-й корзине четное количество
- 6. Задача 2 Может ли конь пройти с
- 7. Решение: Всего 64 поля. А1 уже занято.
- 8. Задачи на разбиение на пары Свойство: Если предметы можно разбить на пары, то их количество четно.
- 9. Задача 1Соединили 4 города между собой дорогами,
- 10. Решение (1-й способ) Пусть даны города А, В,
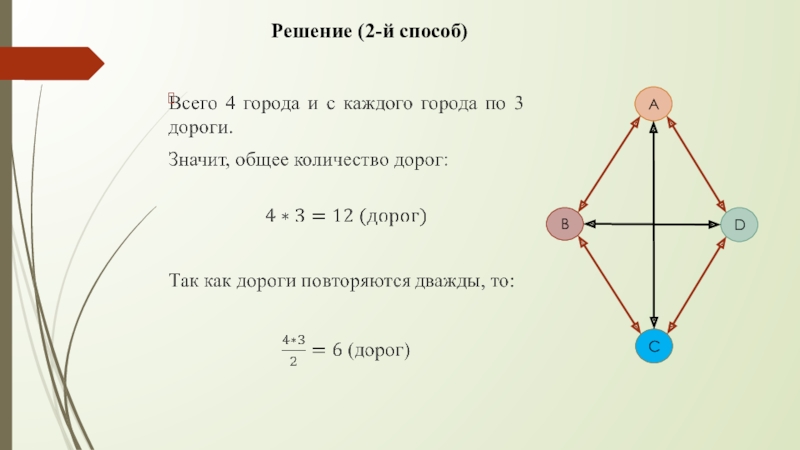
- 11. Решение (2-й способ)
- 12. !!! Задача решается только тогда, когда общее число дорог можно разбить на пары.
- 13. Задача 2Можно ли соединить 15 городов дорогами, так чтобы из каждого города выходило ровно 7 дорог?
- 14. Решение
- 15. Задачи на четность и нечетность Ч
- 16. Задача 1В магазин «Малыш» привезли новые игрушки.
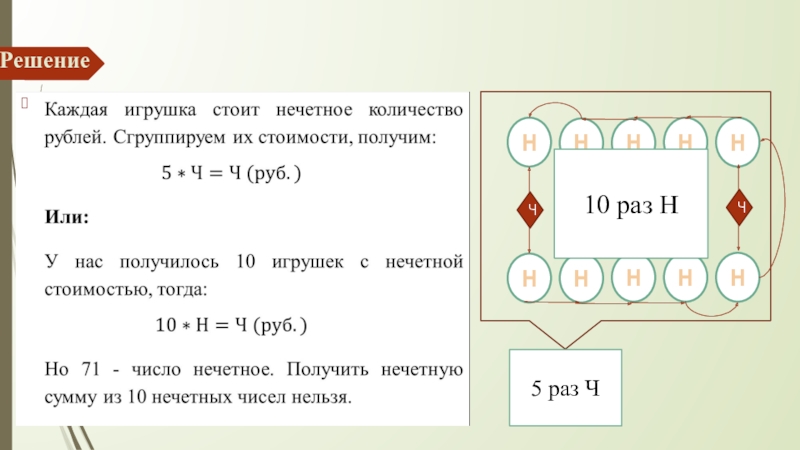
- 17. РешениеННННННННННЧЧЧЧЧ10 раз Н5 раз Ч
- 18. Задача 2Филя перемножил 17 целых чисел и
- 19. Пусть среди 17 чисел все числа четные, тогда:Доказательство (1-й случай):
- 20. Пусть среди 17 чисел найдется хотя бы одно нечетное число, тогда:Доказательство (2-й случай):
- 21. Пусть среди 17 чисел все числа нечетные, тогда: Доказательство (3-й случай):
- 22. Задачи на четность повышенной сложности* На
- 23. Доказательство: Среди чисел 1, 2, ..., 99
- 24. Слайд 24
- 25. Задача 2На волшебной яблоне выросли 15 бананов
- 26. а) В каком порядке надо срывать плоды, чтобы на яблоне остался ровно один плод?
- 27. б) Можно ли срывать плоды так, чтобы
- 28. Задача 3На доске написаны числа 1, 2,
- 29. РешениеМодуль разности двух целых чисел имеет ту
- 30. Задача 4За круглым столом сидят 25 мальчиков
- 31. РешениеДМ
- 32. Задача 5Лиса и два медвежонка делят 100
- 33. РешениеЛиса раскладывает конфеты так: 5, 5 и
- 34. б) Может ли Лиса сделать так, чтобы в итоге съесть ровно 65 конфет??конфет65 конфет100 конфет? конфет
- 35. Задача 6На столе лежит 10 кучек с
- 36. Решение Значит, что общее число орехов нечётно
- 37. Задача 7Придя в школу, Коля и Алиса
- 38. РешениеСгруппируем одинаковые буквы и назовём кратностью то количество
- 39. Задача 8На доске выписаны числа от 1
- 40. Решение1 2 3 4 5 … 50 У нас 25 нечетных чисел и 25 четных.
- 41. Задача 9Среди n рыцарей каждые двое – либо друзья,
- 42. РешениеИз условия следует, что рыцарей – не
- 43. Значит, у каждого рыцаря не более двух
- 44. Задача 10Переаттестация Совета Мудрецов происходит так: король
- 45. РешениеЯсно, что мудрец, стоящий в колонне последним,
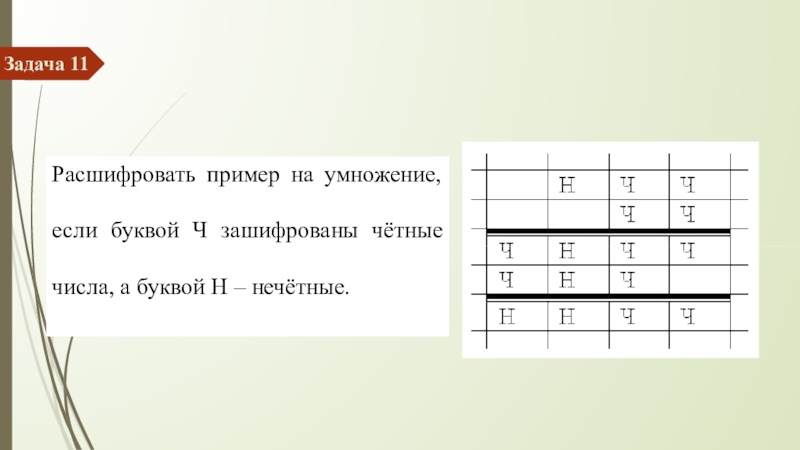
- 46. Задача 11Расшифровать пример на умножение, если буквой
- 47. РешениеЗапишем пример в видеЧ - строчные буквыН - прописные (заглавные) буквы
- 48. Задача 12Существует ли число, которое делится ровно
- 49. Решение
- 50. Задача 13Двое играют в такую игру. Из
- 51. Решениеа) Кто выигрывает при правильной игре –
- 52. Решениеб) Как изменится ответ, если считать, что
- 53. Задача 14На доске записано число 123456789. У
- 54. РешениеЗаметим, что при выполнении каждой операции не
- 55. Задача 15На клетчатой бумаге нарисован замкнутый путь
- 56. РешениеЗаметим, что у нас линия замкнутая. Посчитаем
- 57. Задача 16В плоскости расположено 11 шестерёнок таким
- 58. РешениеПусть первая шестеренка вращается по часовой стрелке,
- 59. Используемая литература Образовательный журнал для старшеклассников и
Слайд 2К задачам на четность относятся:
задачи на чередование
задачи на разбиение на пары
задачи
Слайд 3Задачи на чередование
Свойства:
Если в некоторой замкнутой цепочке чередуются объекты двух
Если в некоторой замкнутой цепочке чередуются объекты двух видов:
начало и конец цепочки разных видов, то в ней четное число объектов;
начало и конец одного вида, то нечетное число.
Обратно:
По четности длины чередующейся цепочки можно узнать, одного или разных видов её начало и конец.
Слайд 4Задача 1
16 корзин расположили по кругу. Можно ли в них разложить
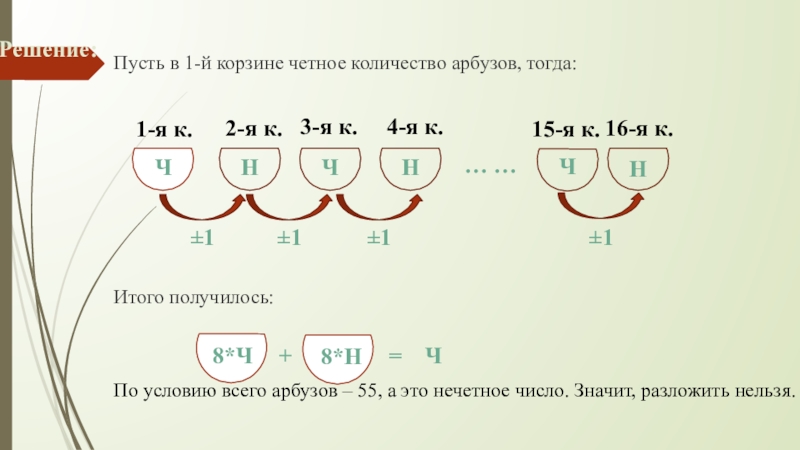
Слайд 5Решение:
Пусть в 1-й корзине четное количество арбузов, тогда:
Итого получилось:
По
Н
Ч
Ч
Н
±1
… …
Н
1-я к.
2-я к.
3-я к.
4-я к.
16-я к.
15-я к.
Ч
±1
±1
±1
Слайд 6Задача 2
Может ли конь пройти с поля a1 на поле
Слайд 7Решение:
Всего 64 поля. А1 уже занято.
Значит, конь должен сделать
1-й ход: белое поле
2-й ход: черное поле
3-й ход: белое поле
4-й ход: черное поле
… … … … … … … …
63-й ход: белое поле
Так как конь должен сделать 63 хода, то последним (нечетным) ходом он встанет на белое поле, а поле h8 черное.
Ответ: нет, не может.
Слайд 8Задачи на разбиение на пары
Свойство:
Если предметы можно разбить на
Слайд 9Задача 1
Соединили 4 города между собой дорогами, так чтобы из каждого
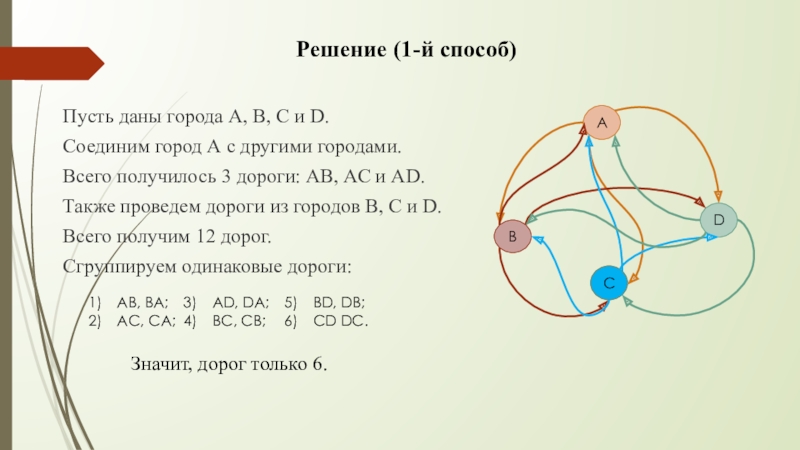
Слайд 10Решение (1-й способ)
Пусть даны города А, В, С и D.
Соединим
Всего получилось 3 дороги: АВ, АС и AD.
Также проведем дороги из городов В, С и D.
Всего получим 12 дорог.
Сгруппируем одинаковые дороги:
А
D
С
В
Значит, дорог только 6.
Слайд 13Задача 2
Можно ли соединить 15 городов дорогами, так чтобы из каждого
Слайд 15Задачи на четность и нечетность
Ч Ч = Ч
Ч
Н Н = Ч
Ч * Ч = Ч
Ч * Н = Ч
Н * Н = Н
Свойства:
Слайд 16Задача 1
В магазин «Малыш» привезли новые игрушки. Могут ли десять игрушек
Слайд 18Задача 2
Филя перемножил 17 целых чисел и получил 1025, а Степашка
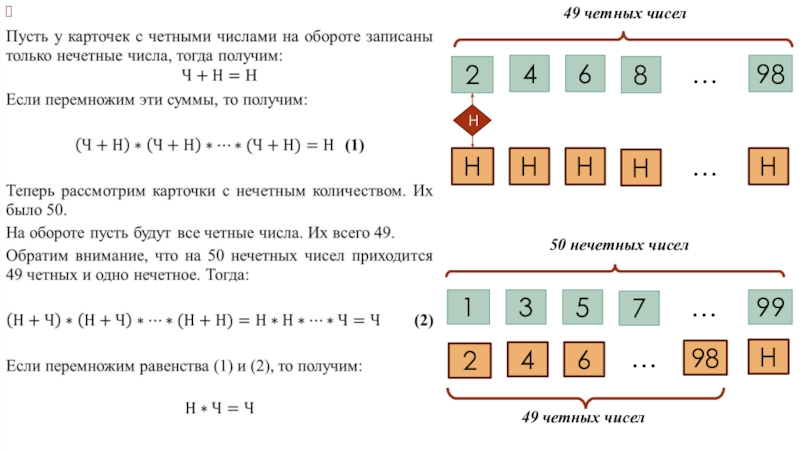
Слайд 20Пусть среди 17 чисел найдется хотя бы одно нечетное число, тогда:
Доказательство
Слайд 22Задачи на четность
повышенной сложности*
На 99 карточках пишутся числа 1,
Задача 1
Слайд 23Доказательство:
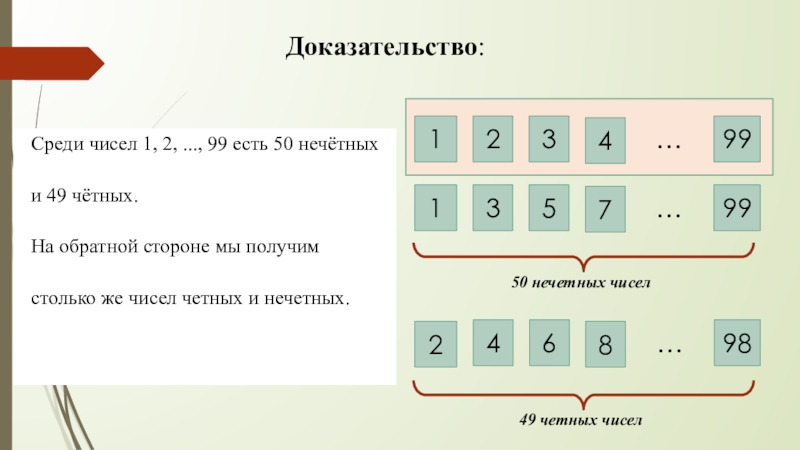
Среди чисел 1, 2, ..., 99 есть 50 нечётных
и 49
На обратной стороне мы получим
столько же чисел четных и нечетных.
1
99
…
3
5
7
1
99
…
2
3
4
2
98
…
4
6
8
Слайд 25Задача 2
На волшебной яблоне выросли 15 бананов и 20 апельсинов. Одновременно
а) В каком порядке надо срывать плоды, чтобы на яблоне остался ровно один плод?
б) Можете ли вы определить, какой это будет плод?
в) Можно ли срывать плоды так, чтобы на яблоне ничего не осталось?
Слайд 27б) Можно ли срывать плоды так, чтобы на яблоне ничего не
Решение:
Всего 15 бананов.
Сорвем 2 банана, останется 13. Еще 2 банана сорвем, останется 11 бананов. Каждый раз число бананов будет нечетным.
В итоге останется 1 банан.
Или:
Всего 15 бананов.
Сорвем 1 банан и 1 апельсин, вырастет 1 банан, т. е. число бананов не изменится.
Слайд 28Задача 3
На доске написаны числа 1, 2, 3, ..., 1984, 1985.
Слайд 29Решение
Модуль разности двух целых чисел имеет ту же чётность, что и
Поэтому, при указанной замене чётность суммы всех чисел не меняется. Сумма целых чисел от 1 до 1985 нечётна (среди них нечётное количество нечётных чисел). Поэтому она не может стать равной нулю.
Ответ:
Не может.
Слайд 30Задача 4
За круглым столом сидят 25 мальчиков и 25 девочек. Докажите,
Слайд 32Задача 5
Лиса и два медвежонка делят 100 конфет. Лиса раскладывает конфеты
а) Придумайте, как Лисе разложить конфеты по кучкам так, чтобы съесть ровно 90 конфет (ни больше, ни меньше).
б) Может ли Лиса сделать так, чтобы в итоге съесть ровно 65 конфет?
Слайд 33Решение
Лиса раскладывает конфеты так: 5, 5 и 90.
Если ей достанется
Если ей достанется кучка из 5 конфет, то, для того чтобы уравнять доли медвежат, ей придётся съесть ещё 85 конфет.
Ответ
а) 5, 5 и 90.
а) Придумайте, как Лисе разложить конфеты по кучкам так, чтобы съесть ровно 90 конфет (ни больше, ни меньше).
5 конфет
90 конфет
100 конфет
5 конфет
Слайд 34б) Может ли Лиса сделать так, чтобы в итоге съесть ровно
?
конфет
65 конфет
100 конфет
? конфет
Слайд 35Задача 6
На столе лежит 10 кучек с 1, 2, 3, 4,
Слайд 36Решение
Значит, что общее число орехов нечётно и перед любым ходом
Ответ
Первый.
Слайд 37Задача 7
Придя в школу, Коля и Алиса обнаружили на доске надпись:
Слайд 38Решение
Сгруппируем одинаковые буквы и назовём кратностью то количество раз, в котором эта
буквы "А" и "О" имеют кратность 3,
буквы "Д", "И", "С" и "Я" – кратность 2, а
буквы "Г", "К", "Л", "М", "Н", "П", "Р", "Т" и "У" – кратность 1.
Чтобы выиграть Алисе, надо:
стереть любую букву кратности 1;
играть так, чтобы после каждого её хода количество букв каждой кратности было чётным.
Например, если Коля сотрёт одну букву "Д", то Алиса может стереть также одну букву "И". Тогда на каждый ход Коли у Алисы будет ответный ход, поэтому именно она сделает последний ход и выиграет.
ААА СС ДД К Р Г У Т Н Л М П ЯЯ ИИ ООО
ГОРОДСКАЯ УСТНАЯ ОЛИМПИАДА
1-й ход Коли
Выигрыш, если стереть последнюю букву
Слайд 39Задача 8
На доске выписаны числа от 1 до 50. Разрешено стереть
Слайд 41Задача 9
Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого
Слайд 42Решение
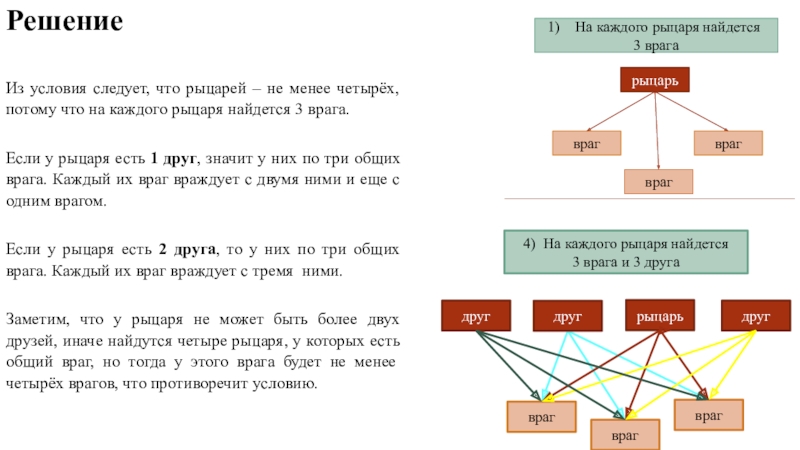
Из условия следует, что рыцарей – не менее четырёх, потому что
Если у рыцаря есть 1 друг, значит у них по три общих врага. Каждый их враг враждует с двумя ними и еще с одним врагом.
Если у рыцаря есть 2 друга, то у них по три общих врага. Каждый их враг враждует с тремя ними.
Заметим, что у рыцаря не может быть более двух друзей, иначе найдутся четыре рыцаря, у которых есть общий враг, но тогда у этого врага будет не менее четырёх врагов, что противоречит условию.
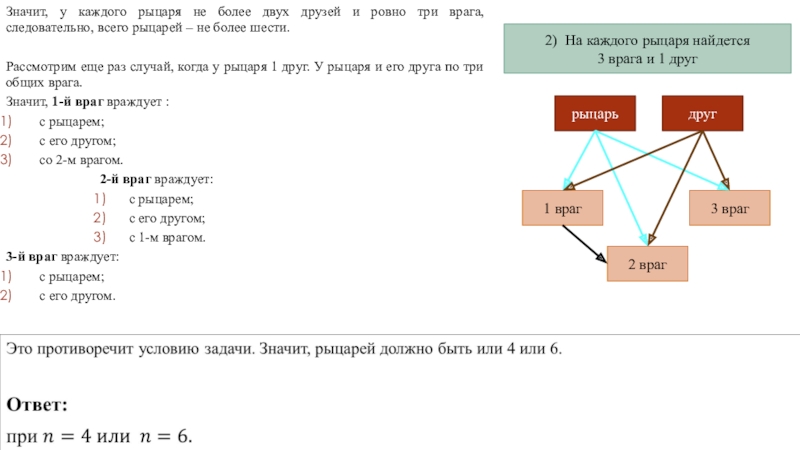
Слайд 43Значит, у каждого рыцаря не более двух друзей и ровно три
Рассмотрим еще раз случай, когда у рыцаря 1 друг. У рыцаря и его друга по три общих врага.
Значит, 1-й враг враждует :
с рыцарем;
с его другом;
со 2-м врагом.
2-й враг враждует:
с рыцарем;
с его другом;
с 1-м врагом.
3-й враг враждует:
с рыцарем;
с его другом.
Слайд 44Задача 10
Переаттестация Совета Мудрецов происходит так:
король выстраивает их в колонну
надевает каждому колпак белого или чёрного цветов.
Все мудрецы видят цвета всех колпаков впереди стоящих мудрецов, а цвет своего и всех стоящих сзади не видят.
Раз в минуту один из мудрецов должен выкрикнуть один из двух цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувшего цвет, отличный от цвета его колпака. Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казнённых.
Скольким из них гарантированно удастся избежать казни?
Слайд 45Решение
Ясно, что мудрец, стоящий в колонне последним, может спастись только случайно,
Но он может спасти всех остальных, сообщив им чётность числа белых колпаков, надетых на них (по договоренности он скажет "белый", если это число нечётно, и "чёрный" в противном случае).
Теперь мудрецы должны вычислять и называть цвета своих колпаков по порядку от предпоследнего к первому:
сначала предпоследний, видя колпаки впереди стоящих и зная чётность числа белых колпаков (среди колпаков впереди стоящих и своего), легко определит цвет своего колпака и назовёт его;
затем мудрец, стоящий перед ним, зная цвета всех тех же колпаков, кроме своего (передние он видит, а про задний только что услышал), по чётности может определить цвет своего колпака и назвать его.
Остается продолжать описанную процедуру до тех пор, пока первый мудрец не определит цвет своего колпака.
Ответ
Всем, кроме одного.
Слайд 46Задача 11
Расшифровать пример на умножение, если буквой Ч зашифрованы чётные числа,
Слайд 48Задача 12
Существует ли число, которое делится ровно на 50 чисел из
Слайд 50Задача 13
Двое играют в такую игру. Из кучки, где имеется 25
а) Кто выигрывает при правильной игре – начинающий или его партнёр? Как он должен играть, чтобы выиграть?
б) Как изменится ответ, если считать, что выигрывает забравший нечётное число спичек?
Слайд 51Решение
а) Кто выигрывает при правильной игре – начинающий или его партнёр?
а) Всегда будет выигрывать второй игрок.
Выигрышная стратегия для второго игрока.
1) всегда брать нечётное число спичек (одну или три);
2) оставлять начинающему число спичек, которое будет делиться без остатка на 4.
Нетрудно проверить, что это возможно. При этом после шести ходов второго игрока у него окажется чётное число спичек, а в кучке останется 0 или
1 спичка.
Слайд 52Решение
б) Как изменится ответ, если считать, что выигрывает забравший нечётное число
б) Всегда будет выигрывать первый игрок.
Выигрышная стратегия для первого игрока.
1) первым ходом взять одну спичку;
2) после этого всегда брать нечётное число спичек (одну или три);
3) оставлять начинающему число спичек, которое будет делиться без остатка на 4.
При этом он сделает ровно 7 ходов, и у него окажется нечётное число спичек.
Слайд 53Задача 14
На доске записано число 123456789. У написанного числа выбираются две
Слайд 54Решение
Заметим, что при выполнении каждой операции не меняется чётность цифры, стоящей
В самом деле, вначале у нас было число 123456789, то есть число вида НЧНЧНЧНЧН (Н означает нечётную цифру, а Ч – чётную).
Если мы возьмём пару соседних цифр, скажем НЧ, то при уменьшении этих цифр на 1 получится пара ЧН, а при смене местами снова получится пара НЧ.
Итак, в процессе выполнения операций число все время будет иметь вид НЧНЧНЧНЧН.
Минимальным числом такого вида является число 101010101.
Осталось показать, что число 101010101 получить можно.
Для этого достаточно в исходном числе 123456789 применить два раза нашу операцию к паре соседних цифр 2 и 3, четыре раза – к паре 4 и 5, шесть раз – операцию к паре 6 и 7 и наконец восемь раз – к паре 8 и 9.
Слайд 55Задача 15
На клетчатой бумаге нарисован замкнутый путь (по линиям сетки). Доказать,
Слайд 56Решение
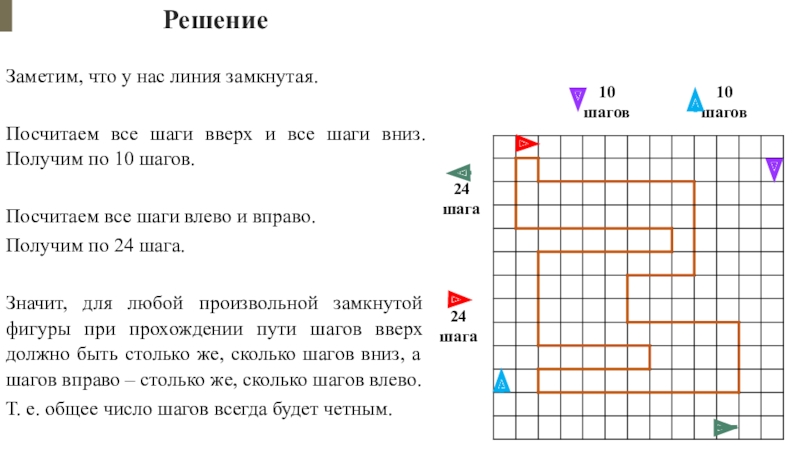
Заметим, что у нас линия замкнутая.
Посчитаем все шаги вверх и
Посчитаем все шаги влево и вправо.
Получим по 24 шага.
Значит, для любой произвольной замкнутой фигуры при прохождении пути шагов вверх должно быть столько же, сколько шагов вниз, а шагов вправо – столько же, сколько шагов влево.
Т. е. общее число шагов всегда будет четным.
10
шагов
10
шагов
24
шага
24
шага
Слайд 57Задача 16
В плоскости расположено 11 шестерёнок таким образом, что первая сцеплена
Могут ли они вращаться?
Слайд 58Решение
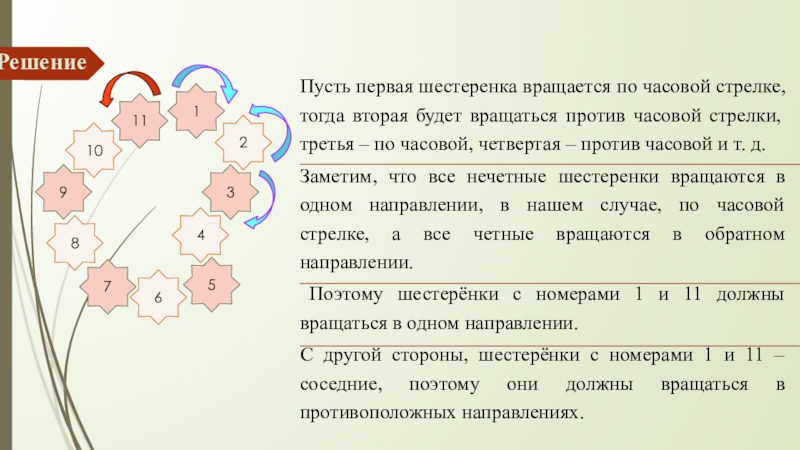
Пусть первая шестеренка вращается по часовой стрелке, тогда вторая будет вращаться
Заметим, что все нечетные шестеренки вращаются в одном направлении, в нашем случае, по часовой стрелке, а все четные вращаются в обратном направлении.
Поэтому шестерёнки с номерами 1 и 11 должны вращаться в одном направлении.
С другой стороны, шестерёнки с номерами 1 и 11 – соседние, поэтому они должны вращаться в противоположных направлениях.
11
1
2
3
4
5
6
7
8
10
9
Слайд 59Используемая литература
Образовательный журнал для старшеклассников и учителей «Потенциал», №1, 2008;
Дориченко
Спивак А.В. "Математический праздник", Москва, МЦНМО, 1995.
http://www.problems.ru