- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему задачи на переливание
Содержание
- 1. Презентация по математике на тему задачи на переливание
- 2. Актуальность: Очень многие факты в математике
- 3. Цель исследования: Знакомство с новым методом решения
- 4. Задачи исследования:- Изучить историю происхождения задач
- 5. Задачи на переливание - это
- 6. Задача Пуассона
- 7. Некто имеет двенадцать пинт вина (ПИНТА- старинная
- 8. задача №1Условие: У нас имеется два сосуда-
- 9. Задача №2Условие: У нас имеется два сосуда-
- 10. Ответ к задаче пуассонаВыполняя лишь операции «наполним
- 11. Задача №3Условие: Как, пользуясь двумя сосудами- семи-
- 12. В рассмотренных о задачах на переливания было
- 13. В первый сосуд входит 8 л и
- 14. В первый сосуд входит 12 л и
- 15. Попробуй прокомментировать действия самостоятельно.Бидон, ёмкость которого 10л,
- 16. Составь таблицу самостоятельно.В таблице надо отразить сколько
- 17. Составь таблицу самостоятельно.В таблице надо отразить сколько
- 18. Вывод: Ценность задач, решаемых с помощью
- 19. Спасибо за внимание!
Слайд 1Задачи на переливания
Выполнила ученица МОУ «СОШ № 56» г. Саратова
6
Макарова Дарья
Руководитель: Прохорова С.А.
Слайд 2
Актуальность: Очень многие факты в математике , часто предлагаются в
Актуальность работы состоит в том, что задачи имеют практический характер. Задачи развивают логическое мышление, заставляют задумываться, подходить к решению какой либо проблемы с разных сторон, выбирать из множества способов решения наиболее простой, легкий путь.
Слайд 3Цель исследования:
Знакомство с новым методом решения задач и изучение материала,
Слайд 4Задачи исследования:
- Изучить историю происхождения задач на переливание;
- Изучить
- Решить задачи вышеназванным методом;
Слайд 5 Задачи на переливание - это задачи, в которых с
Слайд 7Некто имеет двенадцать пинт вина (ПИНТА- старинная мера жидкости, равная примерно
Обсуждение: Эту задачу недаром связывают с именем знаменитого французского математика, механика и физика Симеона Дени Пуассона (1781-1840). Когда Пуассон был ещё очень молод и колебался в выборе жизненного пути, приятель показал ему тексты нескольких задач, с которыми никак не мог справиться сам. Пуассон менее чем за час решил их все до одной. Но особенно ему понравилась задача про два сосуда.
Эта задача определила мою судьбу,- говорил он впоследствии.- Я решил, что непременно буду математиком.
Прежде чем решать задачу Пуассона, Стоит решить несколько более простых задач.
Слайд 8задача №1
Условие: У нас имеется два сосуда- трёхлитровый и пятилитровый. Нужно,
Ответ: Эту задачу можно решить устно. Наполним трёхлитровый сосуд, перельём из него воду в пятилитровый. Вновь наполним трёхлитровый сосуд и будем переливать воду оттуда в пятилитровый сосуд до тех пор, пока он не наполнится до краёв. При этом в трёхлитровом сосуде останется 1 л. воды.
Слайд 9Задача №2
Условие: У нас имеется два сосуда- трёхлитровый и пятилитровый. Нужно,
Ответ: Выполняя лишь операции «наполним меньший сосуд», «перельём из меньшего сосуда в большей» , получим последовательность: 0-0; 3-0; 0-3; 3-3; 6.
Слайд 10Ответ к задаче пуассона
Выполняя лишь операции «наполним больший сосуд», «перельём из
0-0; 8-0; 3-5; 3-0; 0-3; 8-3; 6-5.
Слайд 11Задача №3
Условие: Как, пользуясь двумя сосудами- семи- и двенадцатилитровым, получить 1л
Ответ: Выполняя лишь операции «наполним меньший сосуд», «перельём из меньшего сосуда в большей» и «опорожним больший сосуд» , получим последовательность: 7-0, 0-7, 7-7, 2-12, 2-0, 0-2, 7-2, 0-9, 7-9, 4-12, 4-0, 0-4, 7-4, 0-11, 7-11, 6-12, 6-0, 0-6,7-6, 1-12.
Слайд 12В рассмотренных о задачах на переливания было дано два сосуда и
В новых заданиях не два сосуда, а три или больше. Воду берут НЕ из водопроводного крана. В таких задачах вода уже есть в каком-то сосуде, например, в самом большом. А маленькими ёмкостями мы будем переливать воду. Выливать воду нельзя. Если необходимо освободить сосуд, то лишнюю воду выливают в другой сосуд. Обычно больший сосуд – это хранилище откуда берут воду и в него сливают лишнюю.
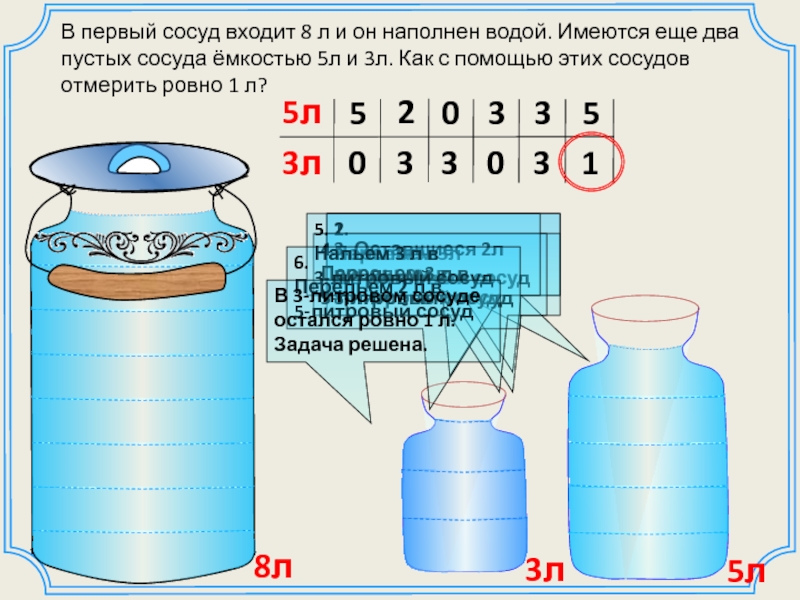
Слайд 13В первый сосуд входит 8 л и он наполнен водой. Имеются
3л
5л
8л
1.
Нальем 5л
в 5-литровый сосуд
2.
Перельем 3л
в 3-литровый сосуд
3. Оставшиеся 2л перельем в
8-литровый сосуд
4.
Перельем 3 л в
5-литровый сосуд
5.
Нальем 3 л в
3-литровый сосуд
6.
Перельем 2 л в
5-литровый сосуд
В 3-литровом сосуде остался ровно 1 л. Задача решена.
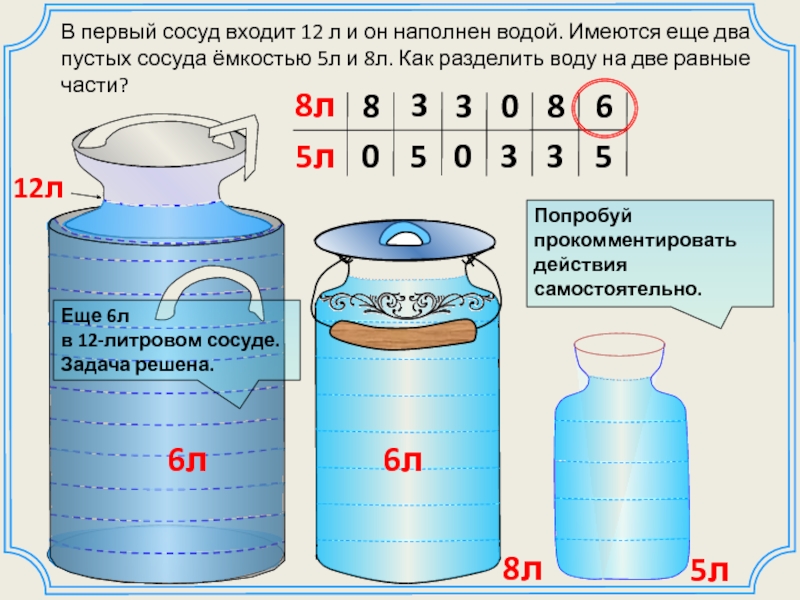
Слайд 14В первый сосуд входит 12 л и он наполнен водой. Имеются
12л
8л
Попробуй прокомментировать действия самостоятельно.
5л
6л
6л
Еще 6л
в 12-литровом сосуде. Задача решена.
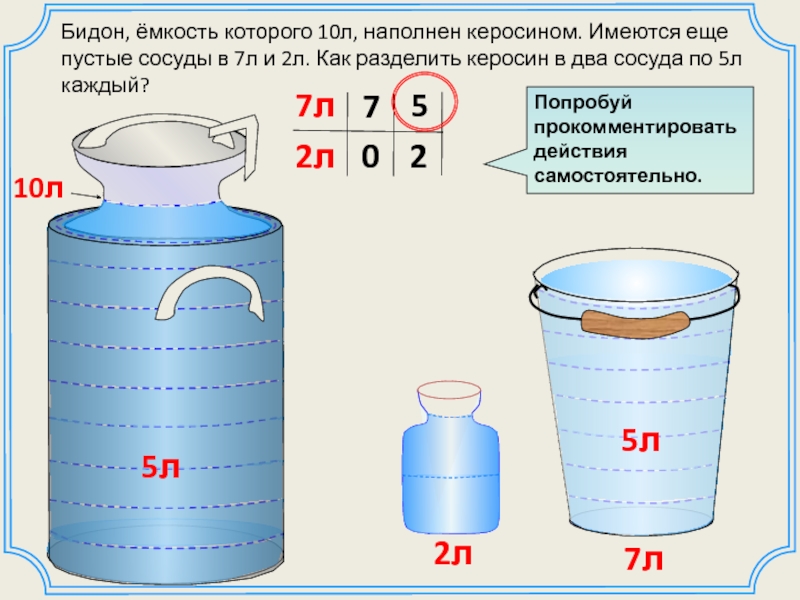
Слайд 15Попробуй прокомментировать действия самостоятельно.
Бидон, ёмкость которого 10л, наполнен керосином. Имеются еще
7л
2л
10л
5л
5л
Слайд 16Составь таблицу самостоятельно.
В таблице надо отразить сколько
литров воды в каждом
после каждого действия.
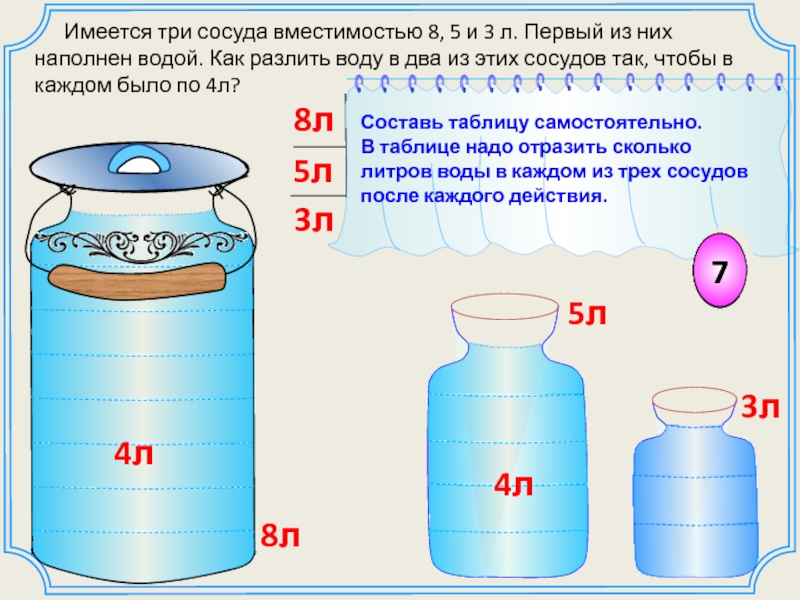
Имеется три сосуда вместимостью 8, 5 и 3 л. Первый из них наполнен водой. Как разлить воду в два из этих сосудов так, чтобы в каждом было по 4л?
3л
5л
8л
1
2
3
4
5
6
4л
4л
7
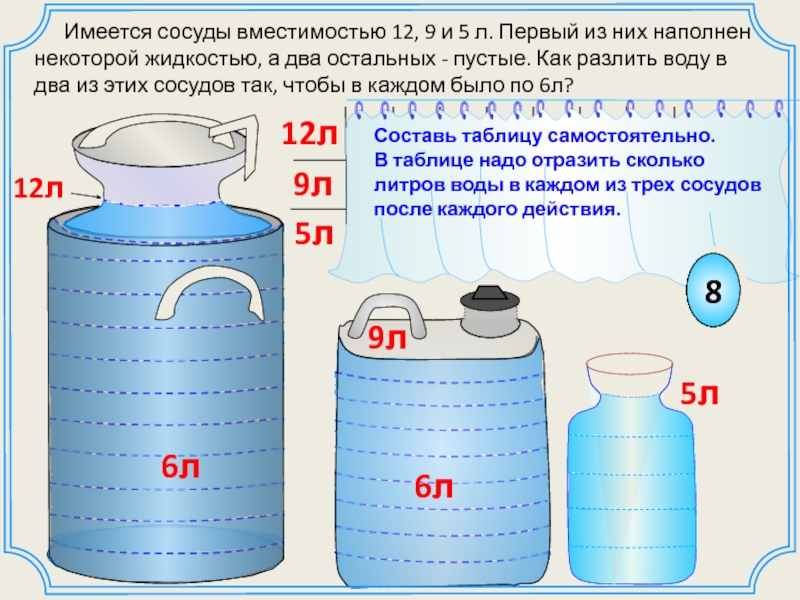
Слайд 17Составь таблицу самостоятельно.
В таблице надо отразить сколько
литров воды в каждом
после каждого действия.
Имеется сосуды вместимостью 12, 9 и 5 л. Первый из них наполнен некоторой жидкостью, а два остальных - пустые. Как разлить воду в два из этих сосудов так, чтобы в каждом было по 6л?
12л
9л
5л
6л
6л
1
2
3
4
5
6
7
8
Слайд 18Вывод:
Ценность задач, решаемых с помощью кругов Эйлера, состоит в
Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Данная тема, безусловно расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных задач. Материал, используемый в работе, пригодится для решения задач занимательного характера, позволит применять методы и правила для решения нетрадиционных задач.