№ 1
.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Векторы
Содержание
- 1. Презентация по математике на тему Векторы
- 2. Понятие вектораОтрезок, для которого указано, какой из
- 3. Понятие вектораЛюбая точка плоскости также является вектором,
- 4. Понятие вектораДлиной или модулем ненулевого вектора АВ
- 5. Сложение векторовПравило треугольника. Пусть а и b
- 6. Сложение векторовПравило параллелограмма. Пусть а и b
- 7. Сложение векторовПравило многоугольника:
- 8. Вычитание векторовРазностью векторов a и b называется
- 9. Вычитание векторовВторой способ. Вычитаемый вектор заменить противоположным
- 10. Умножение вектора на число Для любых чисел
- 11. Вектора в пространствеДва вектора называются равными, если они сонаправлены и их длины равны.
- 12. Вектора в пространствеТеорема: от любой точки можно
- 13. Векторы в физикеВекторы — мощный инструмент физики.
- 14. Векторы в физикеВекторная запись используется при работе
- 15. Векторы в физикеВ физике можно складывать только
- 16. Применение векторов в жизниВекторы интенсивно применяются при
- 17. Применение векторов в жизни
- 18. Применение векторов в жизни
- 19. Применение векторов в жизни
- 20. Применение векторов в жизни
- 21. Применение векторов в жизни
Понятие вектораОтрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.На рисунках вектор изображается отрезком со стрелкой. А обозначают так:
Слайд 1Векторы.
Презентацию подготовила: Седых Светлана Вениаминовна
Учительница математики МКОУ Бобровская средняя
общеобразовательная школа
Слайд 2Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом,
а какой - концом, называется направленным отрезком или вектором.
На рисунках вектор изображается отрезком со стрелкой. А обозначают так: Вектор АВ, А – начало вектора, В – конец. Также векторы можно изображать так:
На рисунках вектор изображается отрезком со стрелкой. А обозначают так: Вектор АВ, А – начало вектора, В – конец. Также векторы можно изображать так:
АВ
А
В
a
b
c
Слайд 3Понятие вектора
Любая точка плоскости также является вектором, который называется НУЛЕВЫМ. Начало
нулевого вектора совпадает с его концом: ММ = 0.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть сонаправленными или противоположно направленными.
Нулевой вектор считается коллинеарным любому вектору.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть сонаправленными или противоположно направленными.
Нулевой вектор считается коллинеарным любому вектору.
М
Слайд 4Понятие вектора
Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ:
АВ = а = АВ.
Длина нулевого вектора считается равной нулю: ММ = 0.
Длина нулевого вектора считается равной нулю: ММ = 0.
a
А
В
М
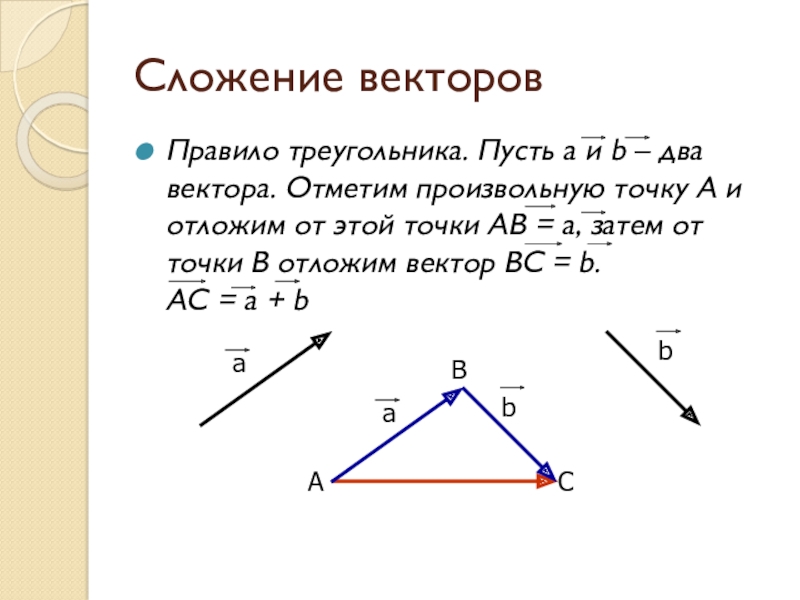
Слайд 5Сложение векторов
Правило треугольника. Пусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b. АС = а + b
a
b
a
b
A
B
C
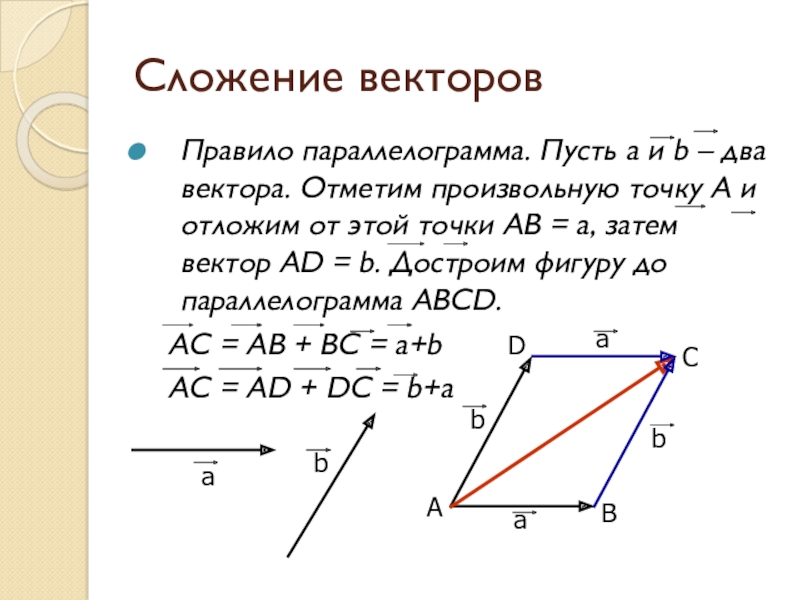
Слайд 6Сложение векторов
Правило параллелограмма. Пусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой точки АВ = а, затем вектор АD = b. Достроим фигуру до параллелограмма АВСD.
АС = АВ + BС = a+b
АС = АD + DС = b+a
АС = АВ + BС = a+b
АС = АD + DС = b+a
a
a
a
b
b
b
A
B
C
D
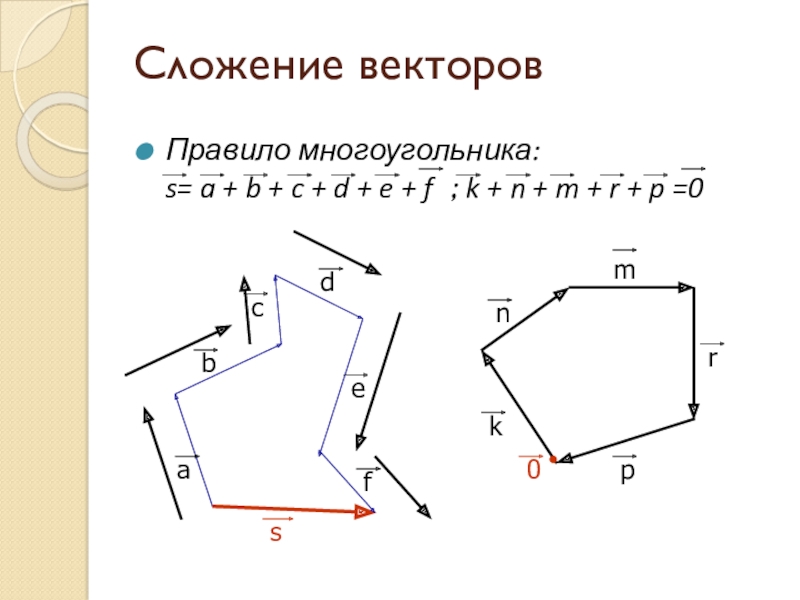
Слайд 7Сложение векторов
Правило многоугольника:
s= a + b + c + d + e + f ; k + n + m + r + p =0
s
0
a
b
c
d
e
f
k
n
m
r
p
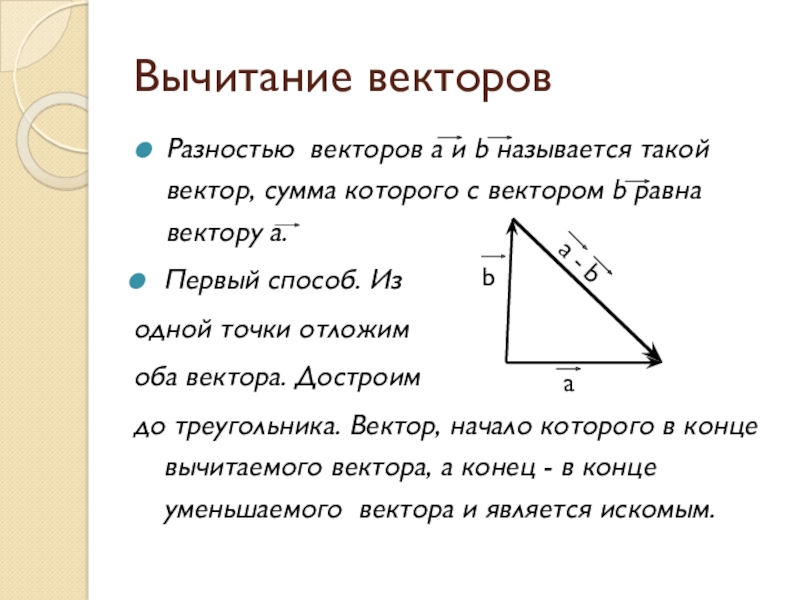
Слайд 8Вычитание векторов
Разностью векторов a и b называется такой вектор, сумма которого
с вектором b равна вектору a.
Первый способ. Из
одной точки отложим
оба вектора. Достроим
до треугольника. Вектор, начало которого в конце вычитаемого вектора, а конец - в конце уменьшаемого вектора и является искомым.
Первый способ. Из
одной точки отложим
оба вектора. Достроим
до треугольника. Вектор, начало которого в конце вычитаемого вектора, а конец - в конце уменьшаемого вектора и является искомым.
a - b
b
a
Слайд 9Вычитание векторов
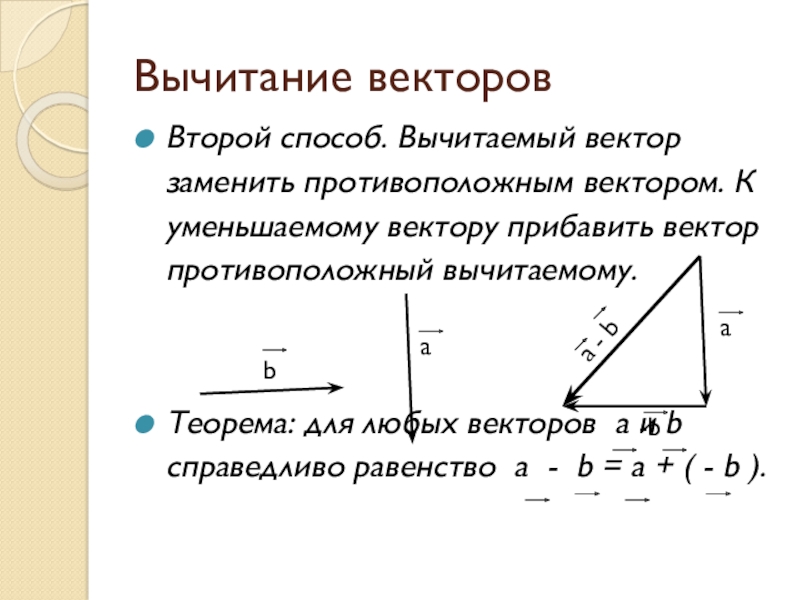
Второй способ. Вычитаемый вектор заменить противоположным вектором. К уменьшаемому вектору
прибавить вектор противоположный вычитаемому.
Теорема: для любых векторов a и b справедливо равенство а - b = а + ( - b ).
Теорема: для любых векторов a и b справедливо равенство а - b = а + ( - b ).
a - b
a
a
b
-b
Слайд 10Умножение вектора на число
Для любых чисел k, n и любых
векторов а, b справедливы равенства:
(kn) а = k (na) (сочетательный закон)
(k+n) а = kа + na (первый распределительный закон)
k ( а+ b ) = kа + kb (второй распределительный закон)
(kn) а = k (na) (сочетательный закон)
(k+n) а = kа + na (первый распределительный закон)
k ( а+ b ) = kа + kb (второй распределительный закон)
Слайд 11Вектора в пространстве
Два вектора называются равными, если они сонаправлены и их
длины равны.
Слайд 12Вектора в пространстве
Теорема: от любой точки можно отложить вектор, равный данному,
и притом только один.
Дано: а - данный вектор, M – данная точка.
Доказать: MN = a, M – начало вектора MN.
Доказательство:
Проведем через начало и конец вектора а и точку М плоскость α.
В плоскости α построим вектор МN = а.
MN – единственный вектор с началом M, равный вектору а.
MN – искомый вектор.
Теорема доказана.
Дано: а - данный вектор, M – данная точка.
Доказать: MN = a, M – начало вектора MN.
Доказательство:
Проведем через начало и конец вектора а и точку М плоскость α.
В плоскости α построим вектор МN = а.
MN – единственный вектор с началом M, равный вектору а.
MN – искомый вектор.
Теорема доказана.
Слайд 13Векторы в физике
Векторы — мощный инструмент физики. На языке векторов формулируются
основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами.
В физике и математике вектор - это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.
В физике и математике вектор - это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.
Слайд 14Векторы в физике
Векторная запись используется при работе с величинами, которые невозможно
задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки. Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
Слайд 15Векторы в физике
В физике можно складывать только векторы, обладающие одинаковой размерностью.
Мы можем складывать скорость со скоростью, силу с силой, но не имеем права сложить вектор скорости с вектором силы. Правила сложения векторов можно объяснить на двух характерных примерах: сложении перемещений и сложении сил.
Перемещением называется вектор, соединяющий начальное и конечное положения тела.
Перемещением называется вектор, соединяющий начальное и конечное положения тела.
Слайд 16Применение векторов в жизни
Векторы интенсивно применяются при разработке компьютерных игр. Применяются
они не только традиционно - для описания таких величин как сила или скорость, но и в областях, которые казалось бы никак не связаны с векторами: хранение цвета, создание теней.
В биологии, вектор агент, который осуществляет заболевания, такие как комар проведение инфицированной крови от одного пациента к другому.
По определению векторы направляют рекомбинантную ДНК в интактные клетки. Тем не менее для больших генов необходимы другие векторы.
Вирусные векторы также применяют в экспериментальной генной терапии при лечении людей. Человеческие вирусы внедряют новую ДНК в человеческие хромосомы.
В биологии, вектор агент, который осуществляет заболевания, такие как комар проведение инфицированной крови от одного пациента к другому.
По определению векторы направляют рекомбинантную ДНК в интактные клетки. Тем не менее для больших генов необходимы другие векторы.
Вирусные векторы также применяют в экспериментальной генной терапии при лечении людей. Человеческие вирусы внедряют новую ДНК в человеческие хромосомы.