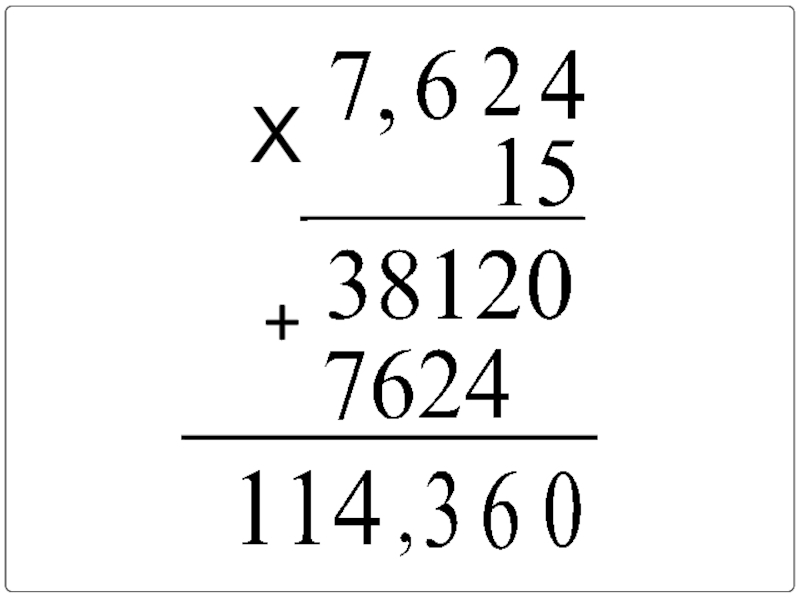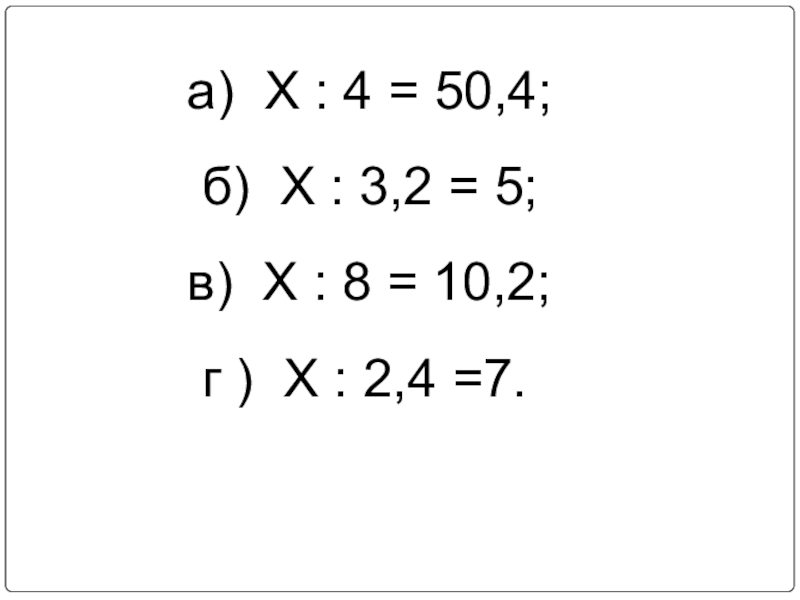классе
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Умножение 5 класс
Содержание
- 1. Презентация по математике на тему Умножение 5 класс
- 2. Цель урока: В увлекательной форме ввести учащимся правило
- 3. Слайд 3
- 4. Слайд 4
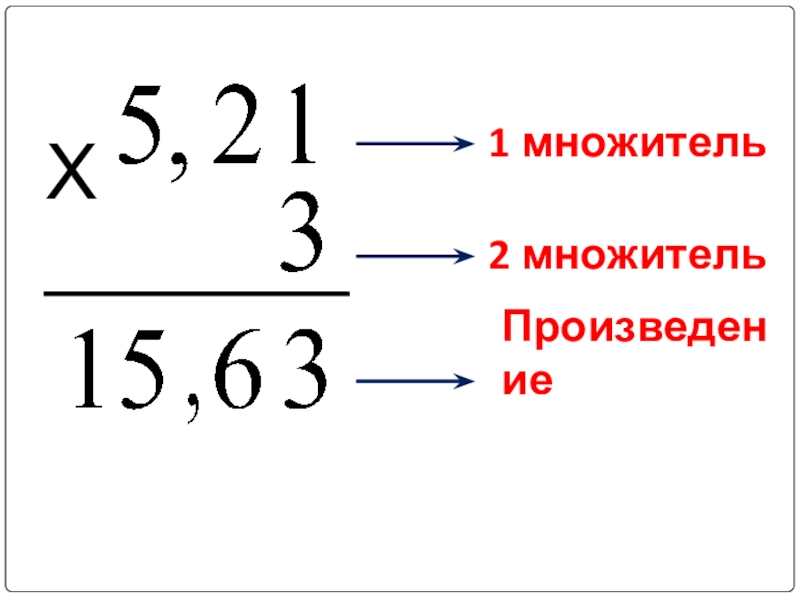
- 5. Х1 множитель2 множительПроизведение
- 6. Х,Чтобы умножить десятичную дробь на натуральное число,
- 7. Х+
- 8. Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч
- 9. а) Х : 4 = 50,4;
- 10. 1. Подумайте, по какому правилу составлен ряд
- 11. 2.В карманах денег поровну. Если
- 12. 3. Какой цифрой заканчивается
- 13. 6. Число, увеличив себя вдвое, посмотрело на
- 14. Расстановка часовыхВдоль стен квадратного бастиона требовалось поставить
- 15. Слайд 15
- 16. Слайд 16
- 17. Молодцы ребята!Большое спасибо!Удачи вам!До свидания!
Цель урока: В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число. Выработать умение применения полученных знаний при решении примеров и задач. Развивать
Слайд 2Цель урока:
В увлекательной форме ввести учащимся правило умножения десятичной дроби на
натуральное число. Выработать умение применения полученных знаний при решении примеров и задач.
Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
Воспитывать интерес к математике, активность, мобильность, умение общаться.
Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
Воспитывать интерес к математике, активность, мобильность, умение общаться.
Слайд 3 Устная работа 1). 7,4 + 3,2= 2,65 + 0,25 = 7,5 – 0,6
=
18,6 + 4,2 =
7,19 – 7,08 =
2). 9 + 9 + 9 + 9 + 9 + 9 +9 =
3.а)х + 2,4 = 5; б) 7,6 – у = 4,2; в) х:8 =9.
Слайд 4 Потерялась запятая 32 + 18 =5; 57 – 4 = 1,7; 3 + 108
= 4,08;
63 – 27 = 60,3.
Помогите вспомнить:
S=ab; Р=2(аb); Р=4а; S=vt.
а) а = 6см., в=9 см., б) а = 8 см.,
в) а=5 см., в = 3 дм., S = 15 ?
Слайд 6Х
,
Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая
внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.
Слайд 101. Подумайте, по какому правилу составлен ряд чисел, и запишите ещё
два числа этого ряда:
А) 1,2; 1,8; 2,4; 3;…
Б) 0,9; 1,8; 3,6; 7,2;…
А) 1,2; 1,8; 2,4; 3;…
Б) 0,9; 1,8; 3,6; 7,2;…
Слайд 11 2.В карманах денег поровну. Если из одного переложить в
другой 3,5 руб., на сколько рублей во втором станет больше?
Слайд 12 3. Какой цифрой заканчивается произведение всех чисел от
7 до 81?
4. Измените запись чисел 2 и 3 так, чтобы получилось число больше 2 и меньше 3.
5. Можно ли пустое ведро наполнить 3 раза подряд, ни разу не опоражнивая.
4. Измените запись чисел 2 и 3 так, чтобы получилось число больше 2 и меньше 3.
5. Можно ли пустое ведро наполнить 3 раза подряд, ни разу не опоражнивая.
Слайд 13
6. Число, увеличив себя вдвое, посмотрело на себя в зеркало и
увидело там 811 . Какое это число?
7.Разделить 10 на 2 части, разность которых 5.
( 9 и 1, 9-1 =8)
7.Разделить 10 на 2 части, разность которых 5.
( 9 и 1, 9-1 =8)
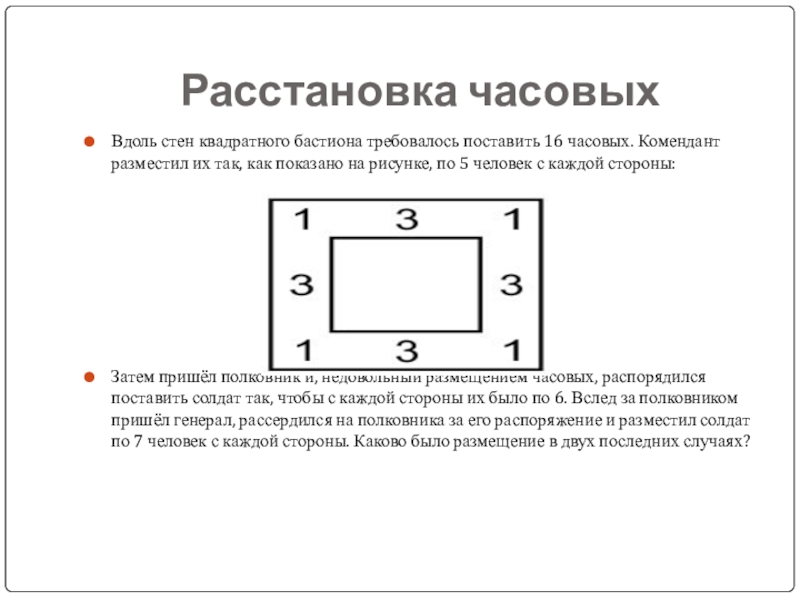
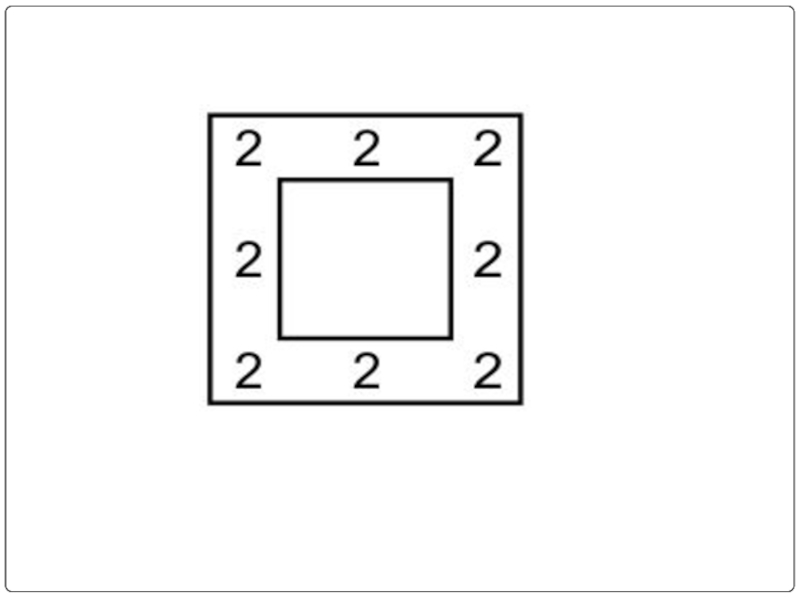
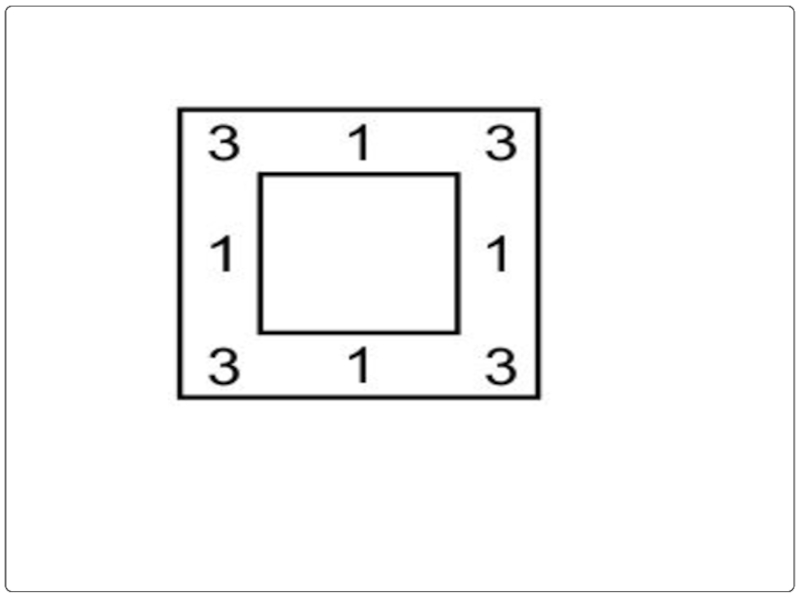
Слайд 14Расстановка часовых
Вдоль стен квадратного бастиона требовалось поставить 16 часовых. Комендант разместил
их так, как показано на рисунке, по 5 человек с каждой стороны:
Затем пришёл полковник и, недовольный размещением часовых, распорядился поставить солдат так, чтобы с каждой стороны их было по 6. Вслед за полковником пришёл генерал, рассердился на полковника за его распоряжение и разместил солдат по 7 человек с каждой стороны. Каково было размещение в двух последних случаях?
Затем пришёл полковник и, недовольный размещением часовых, распорядился поставить солдат так, чтобы с каждой стороны их было по 6. Вслед за полковником пришёл генерал, рассердился на полковника за его распоряжение и разместил солдат по 7 человек с каждой стороны. Каково было размещение в двух последних случаях?