общеобразовательных дисциплин Фирсова Ангелина Александровна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Случайные величины и функции их распределения
Содержание
- 1. Презентация по математике на тему Случайные величины и функции их распределения
- 2. СодержаниеСлучайные величины Дискретная случайная величина (ДСВ)Закон распределения
- 3. Случайные величиныСлучайной величиной (СВ) называется величина, которая
- 4. Дискретная случайная величина (ДСВ)ДСВ – такая величина
- 5. Законом распределения СВ называется соотношение, устанавливающее связь
- 6. 2. Многоугольник распределенияЗакон распределения ДСВPiXix1x2x3x4p1p2p3p4Многоугольник распределенияСумма ординат
- 7. Числовые хар-ки ДСВМатематическое ожидание – сумма произведений
- 8. Числовые хар-ки ДСВСвойства математического ожидания:
- 9. Числовые хар-ки ДСВ2. Дисперсией ДСВХ называется математическое
- 10. Числовые хар-ки ДСВСвойства дисперсии:
- 11. Теоретические моменты ДСВНачальным моментом порядка k СВХ
- 12. Система двух ДСВСистему двух СВ (ХY) можно
- 13. Система двух ДСВТаблица, задающая закон распределения системы двух ДСВ
- 14. Числовые хар-ки системы двух ДСВМатематическое ожидание и
- 15. Непрерывная СВНСВ называется такая величина, возможные значения
- 16. Функция распределения НСВФункцией распределения называют F(x), определяющую
- 17. Функция распределения НСВСвойства функции распределения:если, тоследствие:Если все
- 18. Функция плотности распределения НСВФункцией плотности распределения вероятностей
- 19. Числовые хар-ки НСВМатематическое ожидание НСВХ, все возможные
- 20. Числовые хар-ки НСВСреднеквадратичное отклонение определяется так же,
- 21. Числовые хар-ки НСВЦентральный момент k-ого порядка НСВХ, все возможные значения которой принадлежат интервалу (a:b), определяется равенством:
- 22. Числовые хар-ки НСВЕсли все возможные значения НСВХ
- 23. Кривая распределения СВХГрафик функции f(x) называется кривой
- 24. МодаМодой ДСВХ называется ее наиболее вероятное значение.
- 25. МедианаМедианой НСВХ называется такое ее значение Ме,
- 26. Равномерное распределение плотностиРавномерным называется распределение таких СВ,
- 27. Нормальный закон распределения. Функция ЛапласаНормальный закон распределения
СодержаниеСлучайные величины Дискретная случайная величина (ДСВ)Закон распределения СВЧисловые характеристики ДСВТеоретические моменты ДСВСистема двух ДСВЧисловые характеристики системы двух ДСВНепрерывная СВФункция распределения НСВФункция плотности распределения НСВЧисловые характеристики НСВКривая распределения СВХМодаМедианаРавномерное распределение плотностиНормальный закон распределения. Функция Лапласа
Слайд 1ГБПОУ ВО «Владимирский аграрный колледж»
«Случайные величины и функции их распределения»
Автор: преподаватель
Слайд 2Содержание
Случайные величины
Дискретная случайная величина (ДСВ)
Закон распределения СВ
Числовые характеристики ДСВ
Теоретические моменты
ДСВ
Система двух ДСВ
Числовые характеристики системы двух ДСВ
Непрерывная СВ
Функция распределения НСВ
Функция плотности распределения НСВ
Числовые характеристики НСВ
Кривая распределения СВХ
Мода
Медиана
Равномерное распределение плотности
Нормальный закон распределения. Функция Лапласа
Система двух ДСВ
Числовые характеристики системы двух ДСВ
Непрерывная СВ
Функция распределения НСВ
Функция плотности распределения НСВ
Числовые характеристики НСВ
Кривая распределения СВХ
Мода
Медиана
Равномерное распределение плотности
Нормальный закон распределения. Функция Лапласа
Слайд 3Случайные величины
Случайной величиной (СВ) называется величина, которая в результате опыта может
принять то или иное значение, причем заранее до опыта неизвестно, какое именно.
Делятся на два типа: дискретные СВ (ДСВ) и непрерывные СВ (НСВ)
Делятся на два типа: дискретные СВ (ДСВ) и непрерывные СВ (НСВ)
Слайд 4Дискретная случайная величина (ДСВ)
ДСВ – такая величина ,число возможных испытаний которой
либо конечно, либо бесконечное множество, но обязательно счетное.
Например, частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
ДСВ будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий.
Например, частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
ДСВ будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий.
Слайд 5Законом распределения СВ называется соотношение, устанавливающее связь между возможным значением СВ
и соответствующими вероятностями.
Формы задания закона распределения:
Таблица
Формы задания закона распределения:
Таблица
Закон распределения СВ
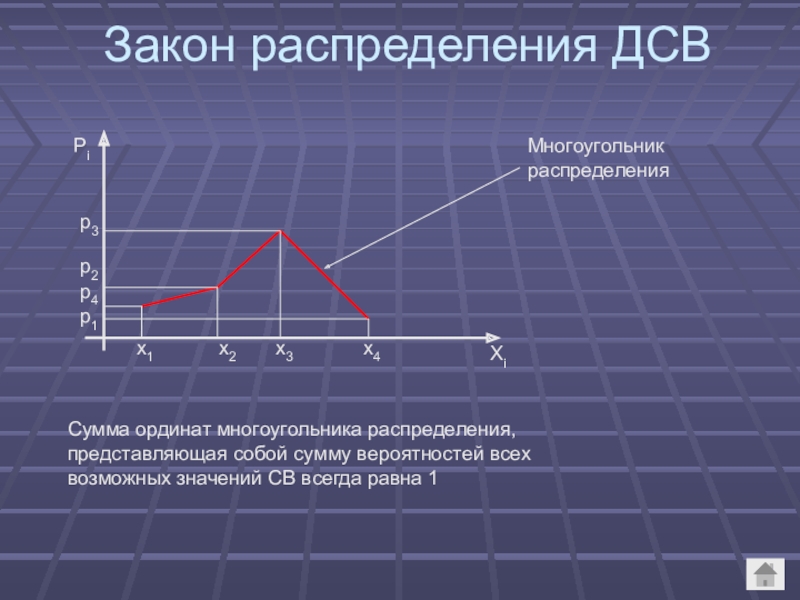
Слайд 62. Многоугольник распределения
Закон распределения ДСВ
Pi
Xi
x1
x2
x3
x4
p1
p2
p3
p4
Многоугольник распределения
Сумма ординат многоугольника распределения, представляющая собой
сумму вероятностей всех возможных значений СВ всегда равна 1
Слайд 7Числовые хар-ки ДСВ
Математическое ожидание – сумма произведений значений СВ на их
вероятности.
Математическое ожидание является хар-кой среднего значения случайной величины
Математическое ожидание является хар-кой среднего значения случайной величины
Слайд 9Числовые хар-ки ДСВ
2. Дисперсией ДСВХ называется математическое ожидание квадрата отклонения случайной
величины от математического ожидания.
Дисперсия характеризует меру рассеяния значений СВ от математического ожидания
При решении задач дисперсию удобно вычислять по формуле:
Дисперсия характеризует меру рассеяния значений СВ от математического ожидания
При решении задач дисперсию удобно вычислять по формуле:
- Среднеквадратичное отклонение
Слайд 11Теоретические моменты ДСВ
Начальным моментом порядка k СВХ называют математическое отношение Хk
Центральным
моментом порядка k СВХ называют математическое ожидание величины
Слайд 12Система двух ДСВ
Систему двух СВ (ХY) можно изображать случайной точкой на
плоскости. Событие, состоящее в попадании случайной точки (ХY) в область D обозначают (X,Y)∩D
Закон распределения системы двух ДСВ можно задать таблицей
Закон распределения системы двух ДСВ можно задать таблицей
Слайд 14Числовые хар-ки системы двух ДСВ
Математическое ожидание и дисперсия системы двух ДСВ
по определению
При решении задач удобно применять формулу
Слайд 15Непрерывная СВ
НСВ называется такая величина, возможные значения которой непрерывно заполняют некоторый
интервал (конечный или бесконечный).
Число всех возможных значений НСВ бесконечно.
Пример: Случайное отклонение по дальности точки падения снаряда от цели.
Число всех возможных значений НСВ бесконечно.
Пример: Случайное отклонение по дальности точки падения снаряда от цели.
Слайд 16Функция распределения НСВ
Функцией распределения называют F(x), определяющую для каждого значения x
вероятность того, что СВХ примет значение, меньшее х, т.е. согласно определению
F(x)=P(XF(x) определяет и ДСВ и НСВ. F(x) также называют интегральной функцией распределения.
F(x)=P(X
Слайд 17Функция распределения НСВ
Свойства функции распределения:
если
, то
следствие:
Если все возможные значения x СВХ
принадлежат интервалу (a;b), то при a<=a F(x)=0, а при x>=b F(x)=0
Следствие:
Следствие:
1.
2.
3.
Функция распределения непрерывна слева
Слайд 18Функция плотности распределения НСВ
Функцией плотности распределения вероятностей называют первую производную от
функции F(x) f(x)=F`(x). f(x) называют дифференциальной функцией. Вероятность того, что НСВХ примет значения, принадлежащие интервалу (a;b) вычисляемые по формуле
Зная плотность распределения, можно найти функцию распределения
Свойства:
, в частности, если все возможные значения СВ принадлежат (a;b), то
1.
2.
Слайд 19Числовые хар-ки НСВ
Математическое ожидание НСВХ, все возможные значения которой принадлежат интервалу
(a;b), определяется равенством:
Дисперсия НСВХ, все возможные значения которой принадлежат интервалу (a;b), определяется равенством:
При решении задач применима формула:
Слайд 20Числовые хар-ки НСВ
Среднеквадратичное отклонение определяется так же, как и для ДСВ:
Начальный
момент k-ого порядка НСВ определяется равенством:
Слайд 21Числовые хар-ки НСВ
Центральный момент k-ого порядка НСВХ, все возможные значения которой
принадлежат интервалу (a:b), определяется равенством:
Слайд 22Числовые хар-ки НСВ
Если все возможные значения НСВХ принадлежат всей числовой оси
ОХ, то во всех вышеуказанных формулах определенный интеграл заменяется несобственным интегралом с бесконечными нижним и верхним пределами
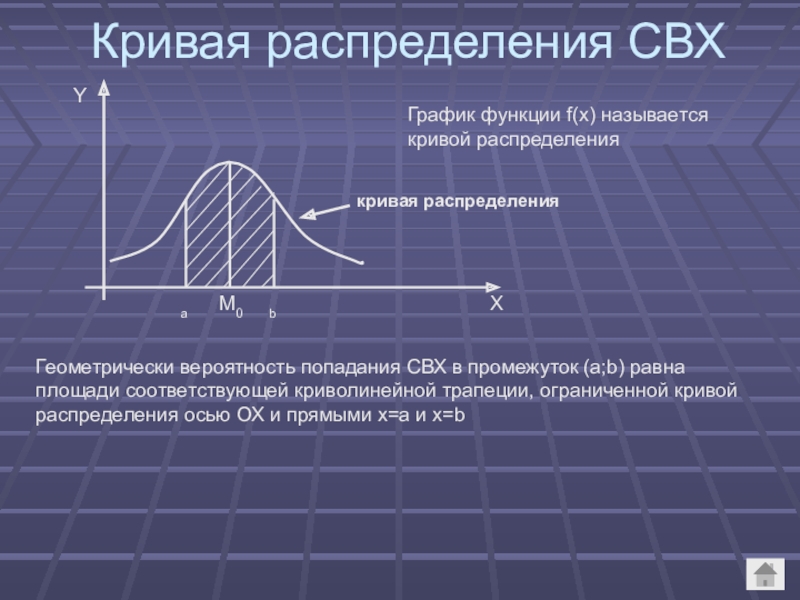
Слайд 23Кривая распределения СВХ
График функции f(x) называется кривой распределения
кривая распределения
Геометрически вероятность попадания
СВХ в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения осью ОХ и прямыми x=a и x=b
Слайд 24Мода
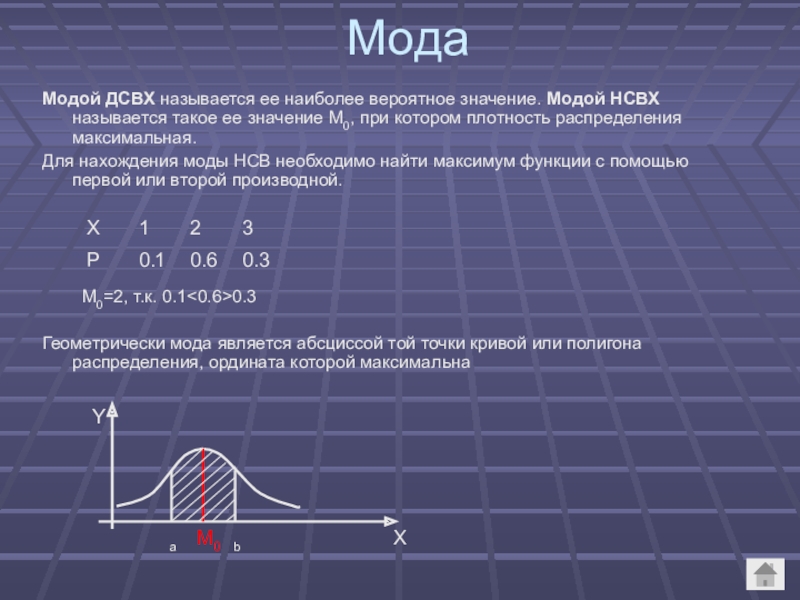
Модой ДСВХ называется ее наиболее вероятное значение. Модой НСВХ называется такое
ее значение M0, при котором плотность распределения максимальная.
Для нахождения моды НСВ необходимо найти максимум функции с помощью первой или второй производной.
M0=2, т.к. 0.1<0.6>0.3
Геометрически мода является абсциссой той точки кривой или полигона распределения, ордината которой максимальна
Для нахождения моды НСВ необходимо найти максимум функции с помощью первой или второй производной.
M0=2, т.к. 0.1<0.6>0.3
Геометрически мода является абсциссой той точки кривой или полигона распределения, ордината которой максимальна
Слайд 25Медиана
Медианой НСВХ называется такое ее значение Ме, для которого одинаково вероятно,
окажется ли случайная величина больше или меньше Ме, т.е. P(x< Ме)=P(x> Ме)=0.5
Ордината, проведенная к точке с абсциссой, равной Ме, делит пополам площадь, ограниченную кривой или полигоном распределения. Если прямая x=a является осью симметрии кривой распределения y=f(x), то М0=Ме=М(Х)=a
Ордината, проведенная к точке с абсциссой, равной Ме, делит пополам площадь, ограниченную кривой или полигоном распределения. Если прямая x=a является осью симметрии кривой распределения y=f(x), то М0=Ме=М(Х)=a
Слайд 26Равномерное распределение плотности
Равномерным называется распределение таких СВ, все значения которых лежат
на некотором отрезке (a;b) и имеют постоянную плотность вероятности на этом отрезке
Математическое ожидание, дисперсия, среднеквадратичное отклонение равномерно распределенной СВ:
Слайд 27
Нормальный закон распределения. Функция Лапласа
Нормальный закон распределения характеризуется плотностью
Кривая распределения симметрична
относительно прямой x=a. Максимальная ордината при x=a равна
Y
X
x=a
Кривая Гаусса, нормальная кривая
Ось абсцисс является асимптотой кривой y=f(x)
Ф(x) - Функция Лапласа
