- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Сетевое планирование и управление для обучающихся колледжа
Содержание
- 1. Презентация по математике на тему Сетевое планирование и управление для обучающихся колледжа
- 2. Тема 6. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ
- 3. Сетевое планирование и управление (СПУ) – это
- 4. Задача сетевого планирования состоит в том, чтобы
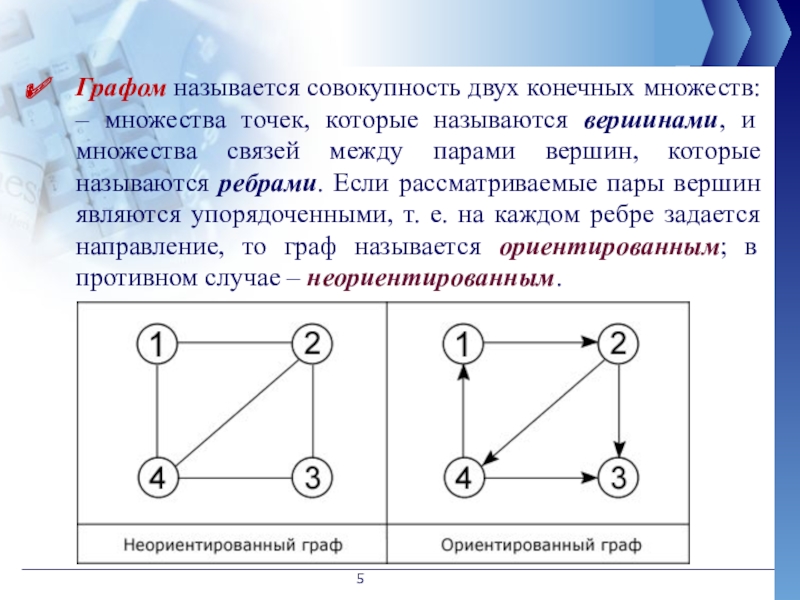
- 5. Графом называется совокупность двух конечных множеств: –
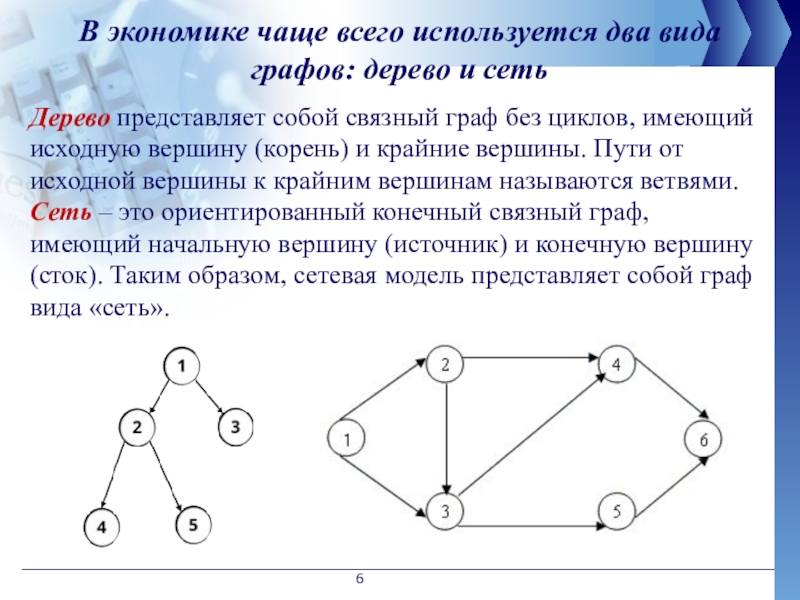
- 6. В экономике чаще всего используется два вида
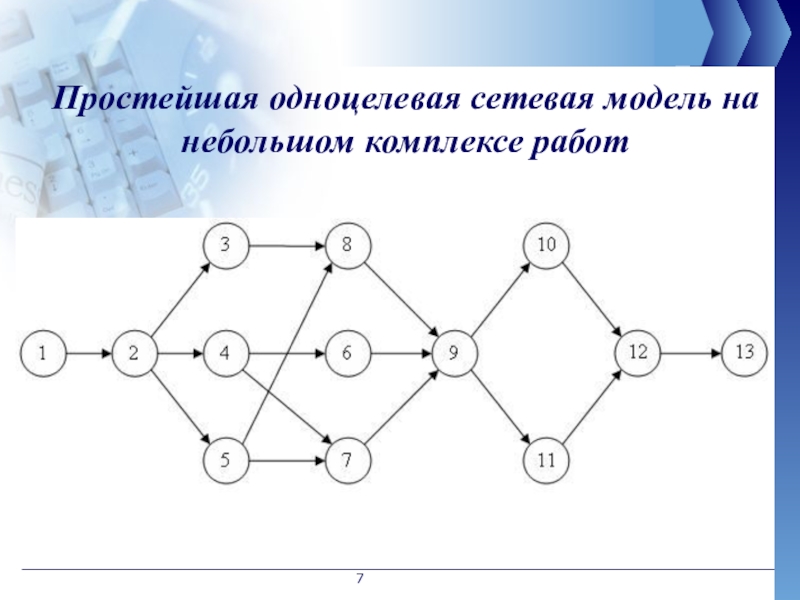
- 7. Простейшая одноцелевая сетевая модель на небольшом комплексе работ
- 8. РАБОТА— это любые процессы (действия), приводящие
- 9. СОБЫТИЯ (кроме исходного) являются результатами выполненных работ.
- 10. Событие в сетевой модели может иметь следующие
- 11. ПУТЬ— это любая последовательность работ в сети,
- 12. СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ
- 13. СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ
- 14. СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО
- 15. СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ
- 16. СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ
- 17. Слайд 17
- 18. TEXTTEXTTEXTTEXTПараметры сетевых графиковб) резервы времени событийРаннее начало
- 19. Параметры сетевых графиков (продолжение)в) резервы времени путей
- 20. по ресурсам (по движению рабочей силы) по
- 21. Интенсив-ности выполнения критических работПерераспределе-ния трудовых ресурсов между
- 22. Add Your TextЗадание Построить сетевой график. Определить
- 23. Сетевой график. Кружком на сетевом графике изображается событие, стрелкой отражается работа. Сверху показываем длительность работ.
- 24. По критическому пути следуют работы 1-2 (длительность
- 25. Для работы 9.10.Раннее начало (ранний срок начала)
- 26. ЗаключениеСетевые модели обладают свойством адаптивности и предвидения,
- 27. Список основной литературы по теме лекции:Агарков, А.П.
- 28. Задание для подготовки к практическому занятию:
Слайд 3Сетевое планирование и управление (СПУ) – это комплекс графических и расчетных
Основная цель сетевого планирования - сокращение до минимума продолжительности проекта.
Слайд 4Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно
Сетевая модель – это план выполнения некоторого комплекса взаимосвязанных работ, заданного в форме сети, графическое изображение которой называется сетевым графиком.
Слайд 5Графом называется совокупность двух конечных множеств: – множества точек, которые называются
Слайд 6В экономике чаще всего используется два вида графов: дерево и сеть
Дерево
Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида «сеть».
Слайд 8 РАБОТА— это любые процессы (действия), приводящие к достижению определенных результатов (событий).
а) действительная работа — работа,
требующая затрат времени и ресурсов;
б) ожидание — процесс, требующий затрат только
времени (сушка, старение, релаксация и т.п.);
в) фиктивная работа, или зависимость, — изображение
логической связи между работами (изображается
пунктирной стрелкой, над которой не проставляется
время или проставляется нуль).
Слайд 9СОБЫТИЯ (кроме исходного) являются результатами выполненных работ.
Событие не является процессом
Наступление события соответствует моменту начала или окончания работ (моменту формирования определенного состояния системы).
Событие для работ может иметь следующие значения:
начальное событие, за которым непосредственно следует данная работа;
2) конечное событие, которому непосредственно предшествует данная работа.
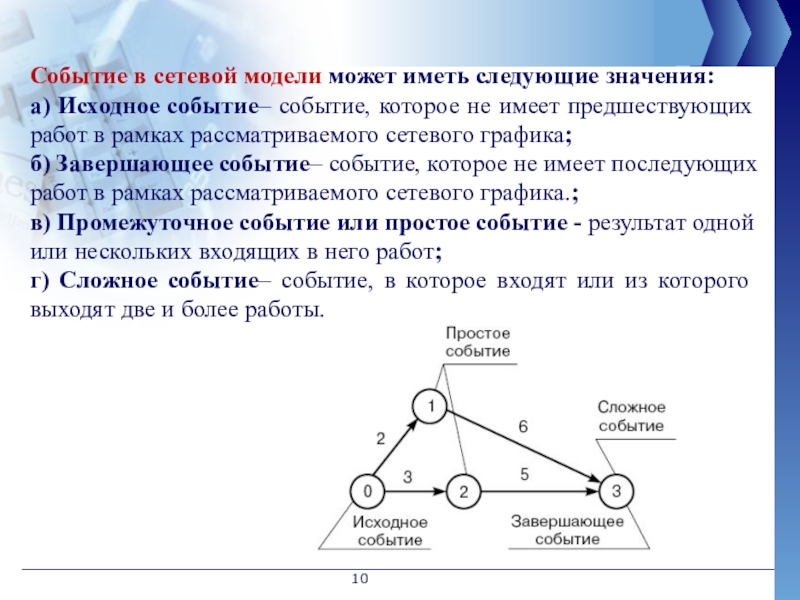
Слайд 10Событие в сетевой модели может иметь следующие значения:
а) Исходное событие– событие,
б) Завершающее событие– событие, которое не имеет последующих работ в рамках рассматриваемого сетевого графика.;
в) Промежуточное событие или простое событие - результат одной или нескольких входящих в него работ;
г) Сложное событие– событие, в которое входят или из которого выходят две и более работы.
Слайд 11ПУТЬ— это любая последовательность работ в сети, в
которой конечное событие
последовательности совпадает с начальным событием
следующей за ней работы.
Полным путем– называют путь от исходного до завершающего
события сетевого графика.
Предшествующий путь– это участок полного пути от исходного
события графика до данного.
Последующий путь– это участок полного пути от данного
события до любого последующего.
Путь описывается последовательностью работ или событий.
Критическим путем– называют полный путь, имеющий
наибольшую длину (продолжительность) из всех полных путей.
Слайд 12
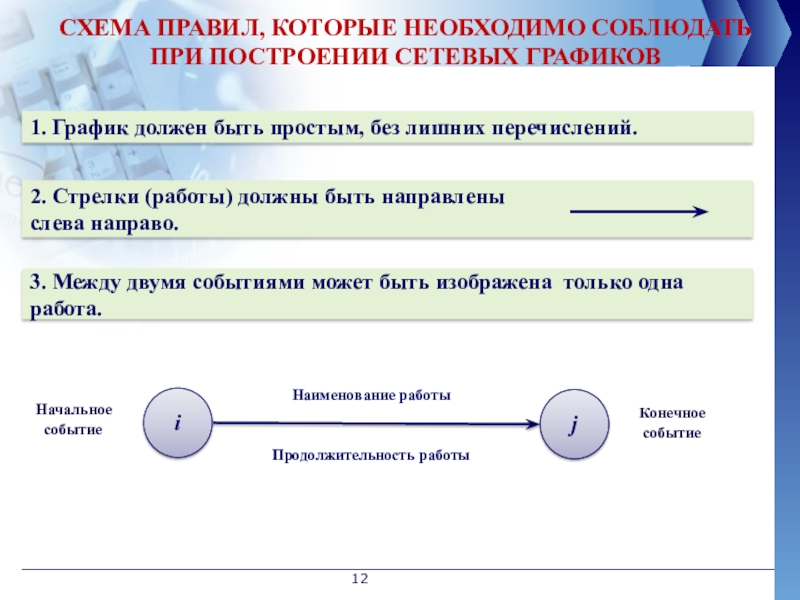
СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ ПОСТРОЕНИИ СЕТЕВЫХ ГРАФИКОВ
1. График должен
2. Стрелки (работы) должны быть направлены
слева направо.
3. Между двумя событиями может быть изображена только одна работа.
i
Слайд 13
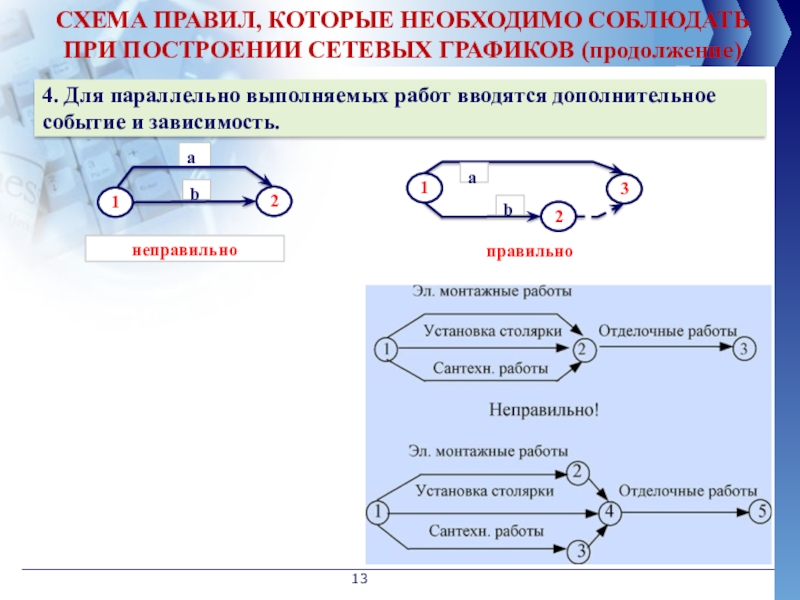
СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ ПОСТРОЕНИИ СЕТЕВЫХ ГРАФИКОВ (продолжение)
4.
Слайд 14
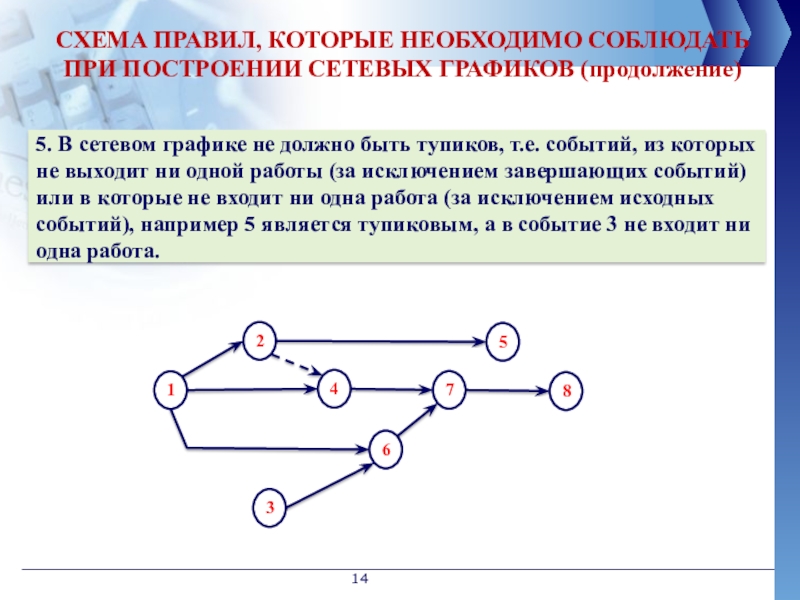
СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ ПОСТРОЕНИИ СЕТЕВЫХ ГРАФИКОВ (продолжение)
5. В
Слайд 15
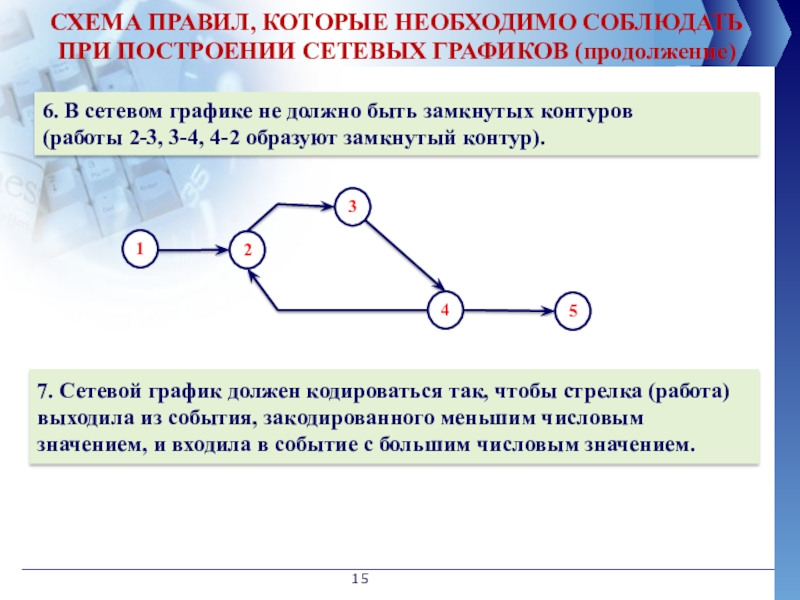
СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ ПОСТРОЕНИИ СЕТЕВЫХ ГРАФИКОВ (продолжение)
6. В
7. Сетевой график должен кодироваться так, чтобы стрелка (работа) выходила из события, закодированного меньшим числовым значением, и входила в событие с большим числовым значением.
Слайд 16
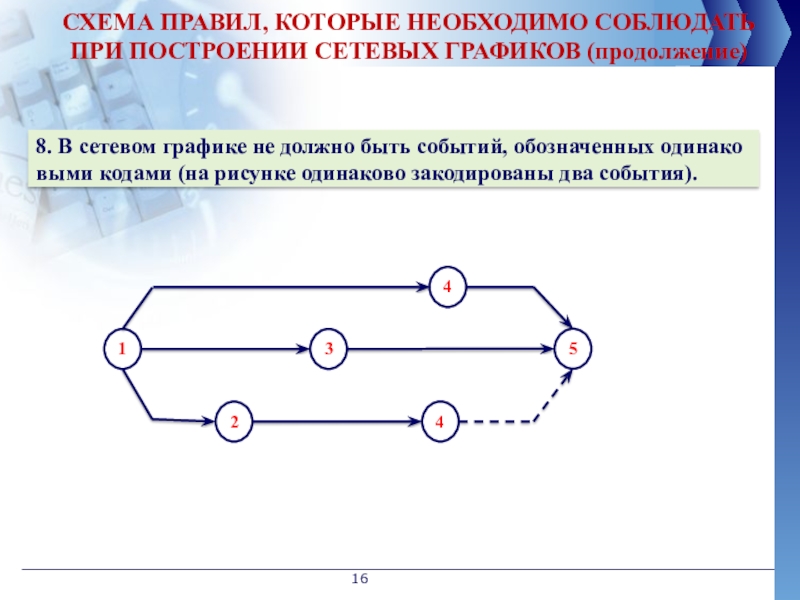
СХЕМА ПРАВИЛ, КОТОРЫЕ НЕОБХОДИМО СОБЛЮДАТЬ ПРИ ПОСТРОЕНИИ СЕТЕВЫХ ГРАФИКОВ (продолжение)
8. В
Слайд 18TEXT
TEXT
TEXT
TEXT
Параметры сетевых графиков
б) резервы времени событий
Раннее начало (ранний срок начала) =
Раннее окончание (ранний срок окончания) = ранее начало + продолжительность работы.
Позднее начало (поздний срок начала) = позднее окончание – продолжительность работы.
Позднее окончание = критический путь – максимальная продолжительность пути от завершающего события всей модели до конечного события рассматриваемой работы.
а) критический путь
Слайд 19Параметры сетевых графиков (продолжение)
в) резервы времени путей и работ
Общий (полный) резерв
Частный (свободный) резерв времени–r – это время, на которое можно увеличить продолжительность работы или позднее ее начать, не меняя при этом ранее начало последующей работы. Частный резерв времени равен или меньше общего резерва времени. Для работ, которые лежат на критическом пути, частный и общий резервы времени равны нулю. Если ранние и поздние характеристики совпадают, то работы лежат на критическом пути.
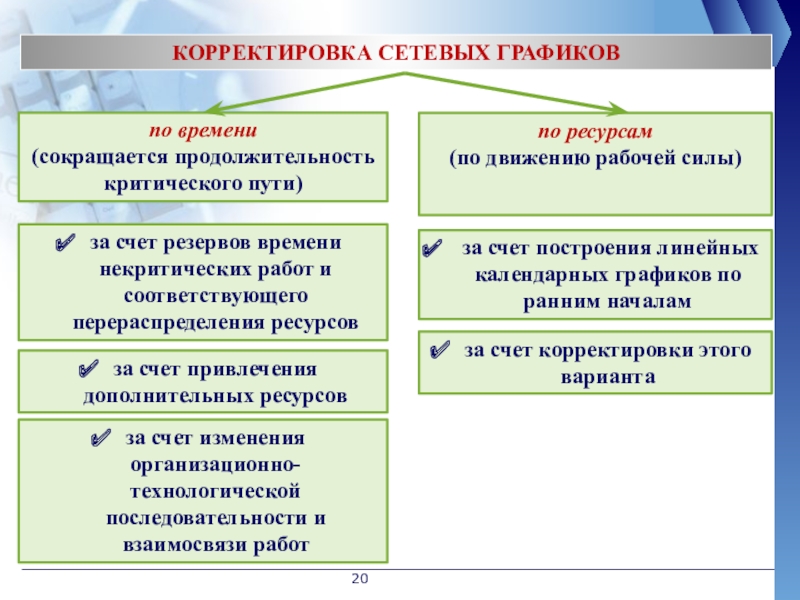
Слайд 20по ресурсам
(по движению рабочей силы)
по времени
(сокращается продолжительность критического
за счет привлечения дополнительных ресурсов
за счет резервов времени некритических работ и соответствующего перераспределения ресурсов
за счет изменения организационно-технологической последовательности и взаимосвязи работ
за счет корректировки этого варианта
за счет построения линейных календарных графиков по ранним началам
КОРРЕКТИРОВКА СЕТЕВЫХ ГРАФИКОВ
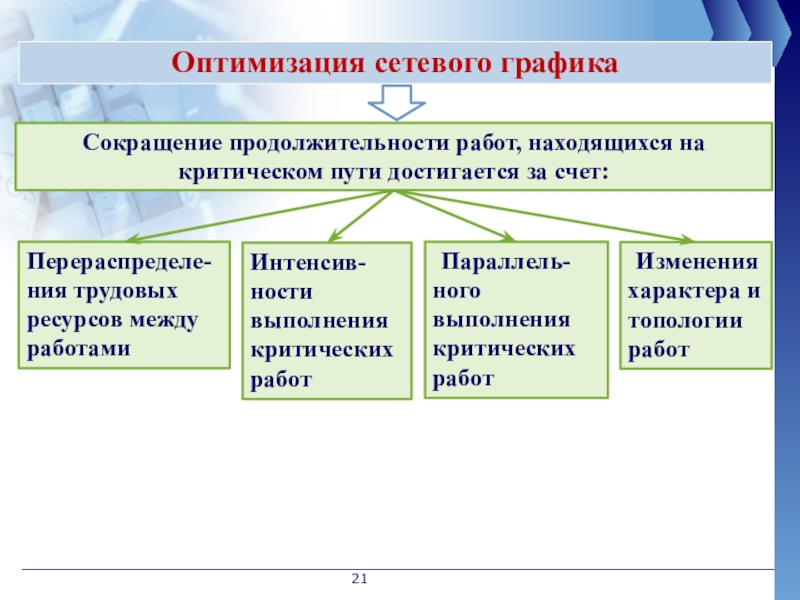
Слайд 21Интенсив-ности выполнения критических работ
Перераспределе-ния трудовых ресурсов между работами
Параллель-ного выполнения критических работ
Оптимизация
Сокращение продолжительности работ, находящихся на критическом пути достигается за счет:
Изменения характера и топологии работ
Слайд 22Add Your Text
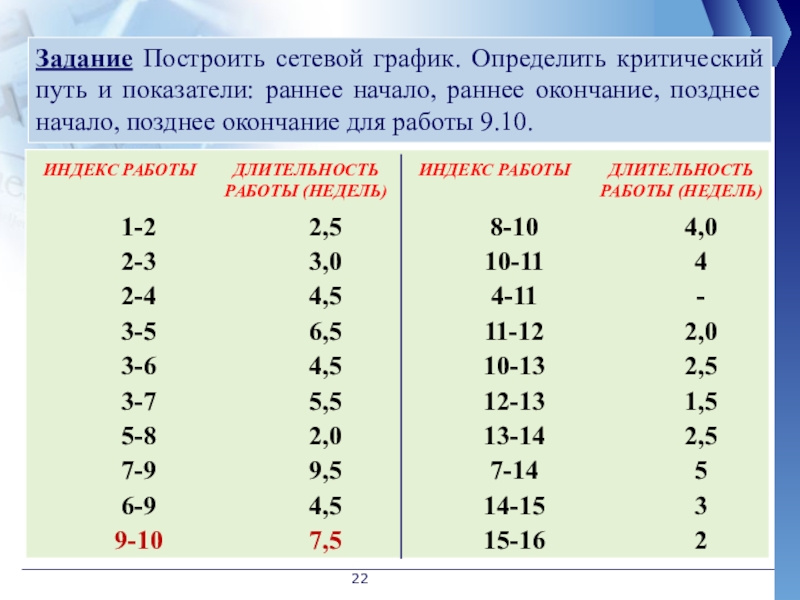
Задание Построить сетевой график. Определить критический путь и показатели:
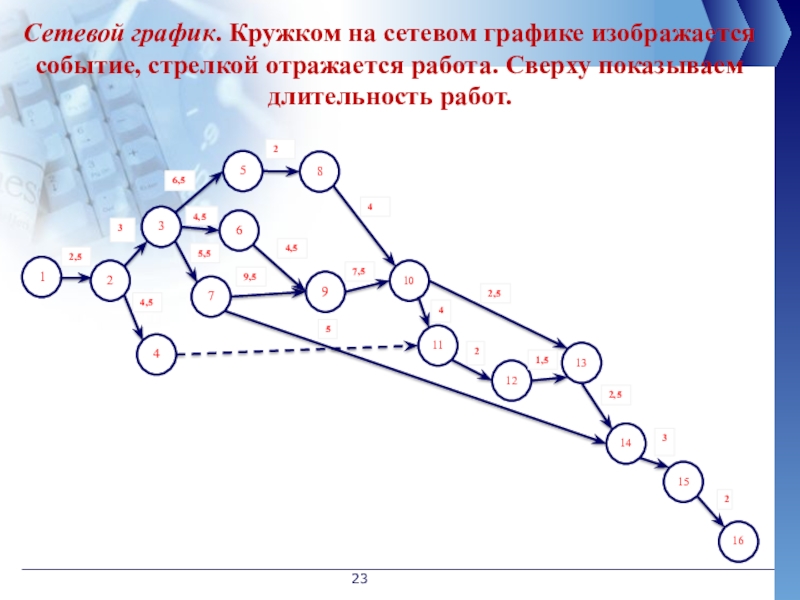
Слайд 23Сетевой график. Кружком на сетевом графике изображается событие, стрелкой отражается работа.
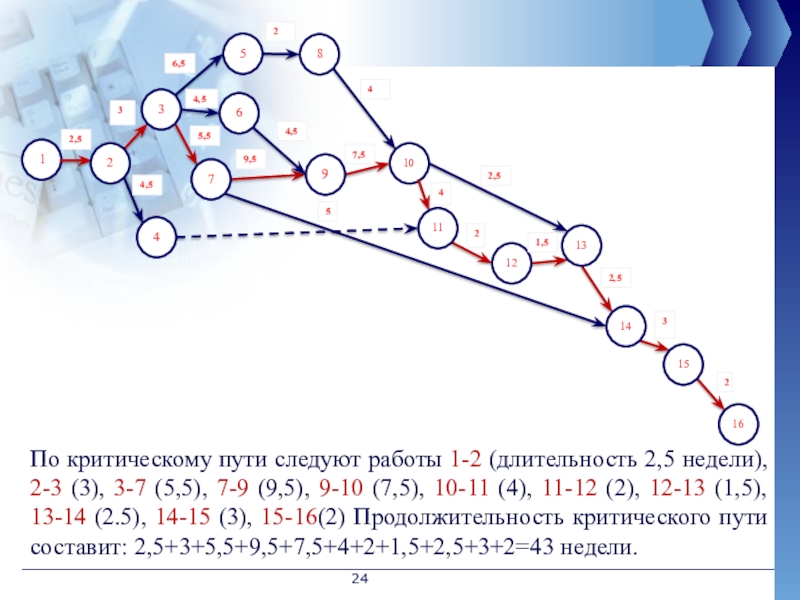
Слайд 24По критическому пути следуют работы 1-2 (длительность 2,5 недели), 2-3 (3),
Слайд 25Для работы 9.10.
Раннее начало (ранний срок начала) = характеризуется выполнением всех
2,5+3+5,5+9,5=20,5 недель
Раннее окончание (ранний срок окончания) = ранее начало + продолжительность рассматриваемой работы
20,5+7,5=28 недель
Позднее начало (поздний срок начала) = позднее окончание – продолжительность рассматриваемой работы
28-7,5=20,5 недель
Позднее окончание = Критический путь – максимальная продолжительность пути от завершающего события всей модели до конечного события рассматриваемой работы
43-15=28 недель
Слайд 26Заключение
Сетевые модели обладают свойством адаптивности и предвидения, поскольку, с одной стороны,
Эффективное применение системы СПУ отражается на экономике и организации труда предприятия. Начинать внедрение СПУ следует с решения относительно простых задач. Степень детализации и структура сетевой модели должны соответствовать производственному процессу и быть удобными для понимания и использования всеми работниками. Используемая информация должна отвечать существующим требованиям и быть нетрудоемкой для ее подготовки.
Слайд 27Список основной литературы по теме лекции:
Агарков, А.П. Теория организации. Организация производства.
Даева, Т.В. Организация и управление производством: практикум. [Электронный ресурс] — Электрон. дан. — Волгоград: Волгоградский ГАУ, 2016. — 88 с. — Режим доступа: http://e.lanbook.com/book/76669
Шамилева Э.Э. Организация производства: учебное пособие для студентов профиля подготовки «Экономика предприятий и организаций» образовательного уровня «бакалавр». - Симферополь, 2017. – 169 с.
Слайд 28
Задание для подготовки к практическому занятию:
Составить перечень работ по выполнению технической
Данные занести в таблицу.











![Презентация по математике на тему Сетевое планирование и управление для обучающихся колледжа Список основной литературы по теме лекции:Агарков, А.П. Теория организации. Организация производства. Список основной литературы по теме лекции:Агарков, А.П. Теория организации. Организация производства. [Электронный ресурс] / А.П. Агарков, Р.С.](/img/thumbs/99f7f434c6d8c8e949aeeb4a094b26e8-800x.jpg)






