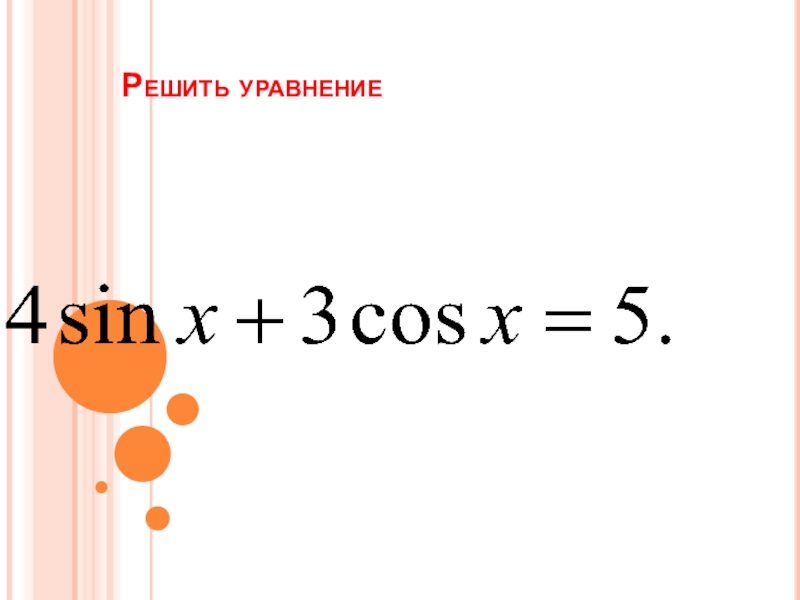Троицкое, 2014 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение тригонометрических уравнений. Повторение.
Содержание
- 1. Презентация по математике на тему Решение тригонометрических уравнений. Повторение.
- 2. Цели урока:-Создания условий для осознанного усвоения решения
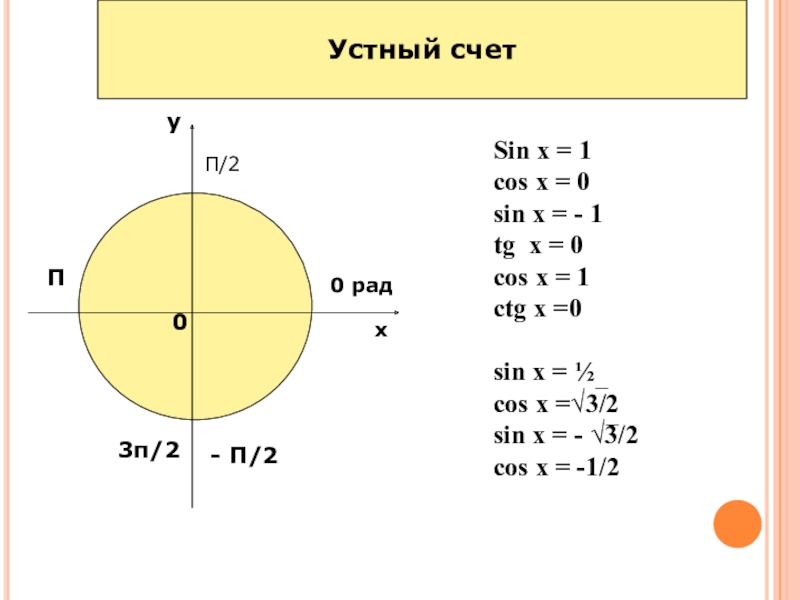
- 3. Устный счетху00 радП/2П- П/23п/2
- 4. Способы решения тригонометрических уравненийУравнения , приводимые к квадратным уравнениямОднородные уравненияРазложение на множителиЗамена переменнойМетод вспомогательного углаПонижение степеней
- 5. Определите вид уравнения и укажите способ его
- 6. Однородные тригонометрические уравнения
- 7. a sin x + b cos x
- 8. Однородные уравнения3sin²x+sinx cos x=2cos²xДелим на sin²x обе
- 9. Решить уравнение sin²x - cos²x = cos4x
- 10. Решение.sin²x-cos²x =cos4x , - (cos² - sin²x
- 11. Решение простейших уравненийРешим уравнение Уравнение однородное, так как степени слагаемых, содержащих переменные одинаковые
- 12. Решение тригонометрических уравнений вида
- 13. Решить уравнение
- 14. Проверьте себя: Здесь
- 15. Замена переменной2(1+tgx) - 3
- 16. Разложение на множители4sin²x-sin2x=04sin²x-2sinx cosx=02sinx(2sinx-cosx)=0Sinx=0 или 2sinx-cosx=0x1=Пn
- 17. Метод вспомогательного углаCos3x+sin3x=1
- 18. Понижение степеней 4
- 19. Спасибо за работу!!!
Цели урока:-Создания условий для осознанного усвоения решения тригонометрических уравнений.-Формирование навыков самоконтроля и взаимоконтроля.-Развитие устной математической речи. Обеспечение условий для развития умения решать тригонометрические уравнения, совершенствовать мыслительные умения старшеклассников: сравнивать, обобщать и анализировать
Слайд 1«Повторение. Решение тригонометрических уравнений».
Проект урока алгебры в 11 классе
Учитель Богдашкина В.А.
С.
Слайд 2Цели урока:
-Создания условий для осознанного усвоения решения тригонометрических уравнений.
-Формирование навыков самоконтроля
и взаимоконтроля.
-Развитие устной математической речи. Обеспечение условий для развития умения решать тригонометрические уравнения, совершенствовать мыслительные умения старшеклассников: сравнивать, обобщать и анализировать
-Развитие устной математической речи. Обеспечение условий для развития умения решать тригонометрические уравнения, совершенствовать мыслительные умения старшеклассников: сравнивать, обобщать и анализировать
Слайд 3Устный счет
х
у
0
0 рад
П/2
П
- П/2
3п/2
Sin x =
1
cos x = 0
sin x = - 1
tg x = 0
cos x = 1
ctg x =0
sin x = ½
cos x =√3/2
sin x = - √3/2
cos x = -1/2
cos x = 0
sin x = - 1
tg x = 0
cos x = 1
ctg x =0
sin x = ½
cos x =√3/2
sin x = - √3/2
cos x = -1/2
Слайд 4Способы решения тригонометрических уравнений
Уравнения , приводимые к квадратным уравнениям
Однородные уравнения
Разложение на
множители
Замена переменной
Метод вспомогательного угла
Понижение степеней
Замена переменной
Метод вспомогательного угла
Понижение степеней
Слайд 5Определите вид уравнения и укажите способ его решения:
а) sin x = 2 cos x;
б) sin x + cos x = 0;
в) 4 cos 3x + 5 sin 3x = 0;
г) 1 +7 cos²x + 3 sin²x = 0;
д) sin 3x – cos 3x = 0;
е) sin x cos x + cos²x = 0
б) sin x + cos x = 0;
в) 4 cos 3x + 5 sin 3x = 0;
г) 1 +7 cos²x + 3 sin²x = 0;
д) sin 3x – cos 3x = 0;
е) sin x cos x + cos²x = 0
Слайд 7a sin x + b cos x = 0, где a
≠ 0, b≠ 0.
При делении уравнения a sin x + b cos x = 0, где a ≠ 0, b≠ 0 на cos x ≠ 0 корни этого уравнения не теряются.
При делении уравнения a sin x + b cos x = 0, где a ≠ 0, b≠ 0 на cos x ≠ 0 корни этого уравнения не теряются.
аsin²x+ bsinx cosx + ccos²x= 0 где а ≠ 0, b ≠ 0, с ≠0.
если в этом уравнении есть одночлен аsin²x, то делим уравнение на cos²x ≠ 0 (так как sinх и cosх одновременно не могут равняться 0).
b sin x cos x + c cos²x = 0 , где b ≠ 0, с ≠0.
(т.е. в уравнении нет одночлена a sin²x), то уравнение решается путем разложения на множители.
Слайд 8Однородные уравнения
3sin²x+sinx cos x=2cos²x
Делим на sin²x обе части уравнения
3+cosx/ sinx=2cos²x/sin²x
Известно ,что
ctg x= cos x/sin x
Получим 3+ctgx=2ctg²x
Пусть a=ctg x
3+a=2a²
2a²-a-3=0
a1=1,5 a2=-1
Получим ctg x=1,5 ctg x=-1
X=arcctg1,5+Пn x=3П/4+Пm
Получим 3+ctgx=2ctg²x
Пусть a=ctg x
3+a=2a²
2a²-a-3=0
a1=1,5 a2=-1
Получим ctg x=1,5 ctg x=-1
X=arcctg1,5+Пn x=3П/4+Пm
Слайд 10Решение.
sin²x-cos²x =cos4x ,
- (cos² - sin²x )=cos4x ,
-cos2x = cos²2x
- sin²2x,
-cos2x = cos²2x – ( 1 - cos²2x),
-cos2x - cos²2x +1 - cos²2x = 0,
-2cos²2x – cos2x +1 = 0,
2cos²2x + cos2x -1 = 0.
Заменим сos2x на У , где |У|1
Тогда 2 у² +у -1 = 0,
D =1 - 4•2•(-1) =9,
У =1/ 2, у = -1.
Выполним обратную замену
Cos2x =1/ 2 , cos2x = -1,
2x = П+2Пn, n € Z,
2x =±arccos1/2 =2Пn , n € Z, x=П/2+Пn, n € Z.
2x ±П/3 +2Пn. n € Z,
X =±П/6+Пn, n € Z.
Ответ: X =±П/6+Пn, x=П/2+Пn, n € Z.
-cos2x = cos²2x – ( 1 - cos²2x),
-cos2x - cos²2x +1 - cos²2x = 0,
-2cos²2x – cos2x +1 = 0,
2cos²2x + cos2x -1 = 0.
Заменим сos2x на У , где |У|1
Тогда 2 у² +у -1 = 0,
D =1 - 4•2•(-1) =9,
У =1/ 2, у = -1.
Выполним обратную замену
Cos2x =1/ 2 , cos2x = -1,
2x = П+2Пn, n € Z,
2x =±arccos1/2 =2Пn , n € Z, x=П/2+Пn, n € Z.
2x ±П/3 +2Пn. n € Z,
X =±П/6+Пn, n € Z.
Ответ: X =±П/6+Пn, x=П/2+Пn, n € Z.
Слайд 11Решение простейших уравнений
Решим уравнение
Уравнение однородное,
так как степени слагаемых,
содержащих
переменные одинаковые
Слайд 14Проверьте себя:
Здесь
Поделим обе части уравнения на 5:
Введем вспомогательный аргумент , такой, что , . Исходное уравнение можно записать в виде
,
,
откуда
Ответ:
Слайд 15Замена переменной
2(1+tgx) - 3 =5
1+tgx
Пусть y=1+tgx
2y - 3 =5
Y
2y²-3=5y
y≠0
2y²-5y-3=0
y1=3 , y2=-0,5
1+tgx=3 1+tgx=-0,5
tgx=2 tgx=-1,5
X 1=arctg2+Пn x 2=-arctg1,5+Пk
Пусть y=1+tgx
2y - 3 =5
Y
2y²-3=5y
y≠0
2y²-5y-3=0
y1=3 , y2=-0,5
1+tgx=3 1+tgx=-0,5
tgx=2 tgx=-1,5
X 1=arctg2+Пn x 2=-arctg1,5+Пk
Слайд 16Разложение на множители
4sin²x-sin2x=0
4sin²x-2sinx cosx=0
2sinx(2sinx-cosx)=0
Sinx=0 или 2sinx-cosx=0
x1=Пn 2sinx
- cosx=0
sinx sinx
2-ctgx=0
ctgx=2
X2=arcctg2+Пk
sinx sinx
2-ctgx=0
ctgx=2
X2=arcctg2+Пk
Слайд 17Метод вспомогательного угла
Cos3x+sin3x=1
√A²+B²=√1²+1²=√2
Делим обе части уравнения на √2
1 cos3x+1 sin3x=1
√2 √2 √2
Пусть cosφ=1/√2 , sinφ=1/√2,φ=П/4
cosφ cos3x+sinφ sin3x=1/√2
Cos(3x-φ)=1/√2
3x-φ=±П/4+2Пn
3x=±П/4+φ+2Пn,
X=±П/12+П/12+2Пn/3
Слайд 18Понижение степеней
4
4
Sin x+cos x=1/2
(Sin²x)²+(cos²x)²=1/2
Известно, что sin²(x/2)=1-cosx, cos²(x/2)=
2
=1+cosx
2
1-cos2x ²+ 1+cos 2x ² = 1
2 2 2
1-2cos2x+cos²2x+1+2cos2x+cos²2x=2
2cos²x=0
cosx=0
X=П/2+Пn
Sin x+cos x=1/2
(Sin²x)²+(cos²x)²=1/2
Известно, что sin²(x/2)=1-cosx, cos²(x/2)=
2
=1+cosx
2
1-cos2x ²+ 1+cos 2x ² = 1
2 2 2
1-2cos2x+cos²2x+1+2cos2x+cos²2x=2
2cos²x=0
cosx=0
X=П/2+Пn