5 класс
Иванова Т.В.
МБОУ «Школа №18»
г. Ростов-на-Дону
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Плоскость. Прямая. Луч. (5 класс)
Содержание
- 1. Презентация по математике на тему Плоскость. Прямая. Луч. (5 класс)
- 2. Примеры плоскостей мы встречаем в жизни постоянно. Это
- 3. А В Нарисуем две точки A и B . Проведем через
- 4. Если прямую AB разделить точкой O, то мы получим два
- 5. Если две прямые имеют общую точку, например O ,
- 6. Н На сколько частей разделяет
- 7. Сколько точек пересечения у прямых AB , CD и
- 8. В скольких точках пересекаются прямая n, луч
- 9. 4. Шкалы и координаты. Правила
- 10. Длины измеряют разными измерительными приборами. Один из
- 11. Шкалы могут быть и на других измерительных
- 12. Нарисуем луч ОХ. Отметим на этом луче точку F. Под началом
- 13. Пишут: О(0), F(1), D(2), E(3) и т. д.
- 14. 1000 г = 1 кг (килограмм);
- 15. Выбери рисунок, на котором градусник показывает 19 °C .
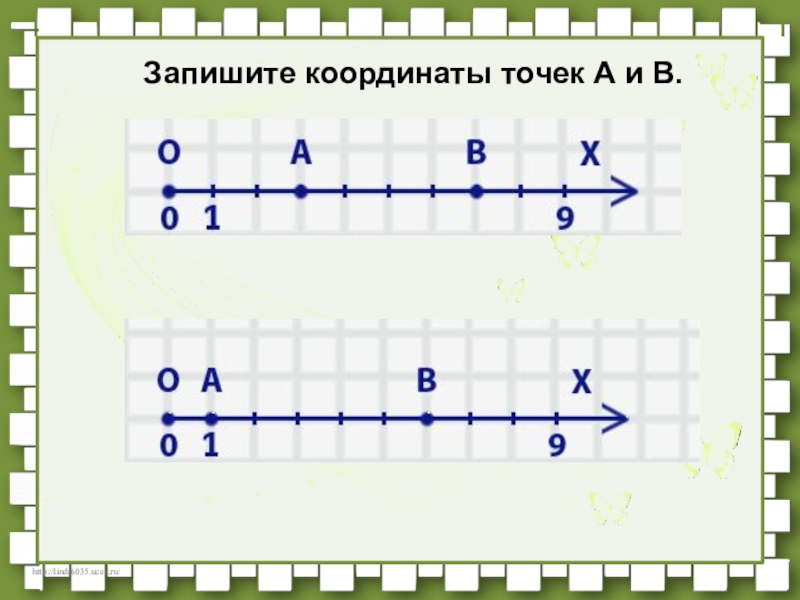
- 16. Запишите координаты точек А и В.
- 17. Какой вес имеют фрукты:
- 18. Выразите в граммах: 1)
- 19. Выразите в килограммах: 1)
- 20. 5. Сравнение чисел. Правила
- 21. При счете натуральные числа называют по порядку: 1,
- 22. Например, точка A(2) лежит левее точки E(6).
- 23. Число 3 меньше, чем 4, и больше, чем 1.
- 24. Многозначные числа сравнивают так. Число 1007 больше, чем 929, потому что
- 25. Меньшее число должно находиться с острого (маленького) конца знака,
- 26. Выберите верное
- 27. Какая из точек А или В лежит правее на координатном луче:
- 28. Какая из точек А или В лежит левее на координатном луче:
- 29. Выберите пять самых маленьких чисел из десяти:
- 30. Выберите пять самых больших чисел из десяти:
Примеры плоскостей мы встречаем в жизни постоянно. Это поверхности окна, парты, школьной доски, но в отличие от этих поверхностей математическая плоскость не ограничена краями. Она простирается бесконечно во все стороны.
Слайд 13. Плоскость. Прямая.
Луч.
5. Сравнение чисел.
4. Шкалы и координаты.
Слайд 2Примеры плоскостей мы встречаем в жизни постоянно.
Это поверхности окна, парты, школьной
доски, но в отличие от этих поверхностей математическая плоскость не ограничена краями.
Она простирается бесконечно во все стороны.
Она простирается бесконечно во все стороны.
Слайд 3
А
В
Нарисуем две точки A и B .
Проведем через них по линейке
линию как
на рисунке.
У нас получилась прямая, которую обозначают прямая AB или прямая BA .
У нас получилась прямая, которую обозначают прямая AB или прямая BA .
Через любые две точки проходит одна единственная прямая.
Прямая не имеет концов.
Она неограниченно продолжается в обе стороны.
Точки A и B лежат на прямой.
Слайд 4 Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA .
Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее.
В отличие от прямой луч бесконечен только в одну сторону.
А
В
О
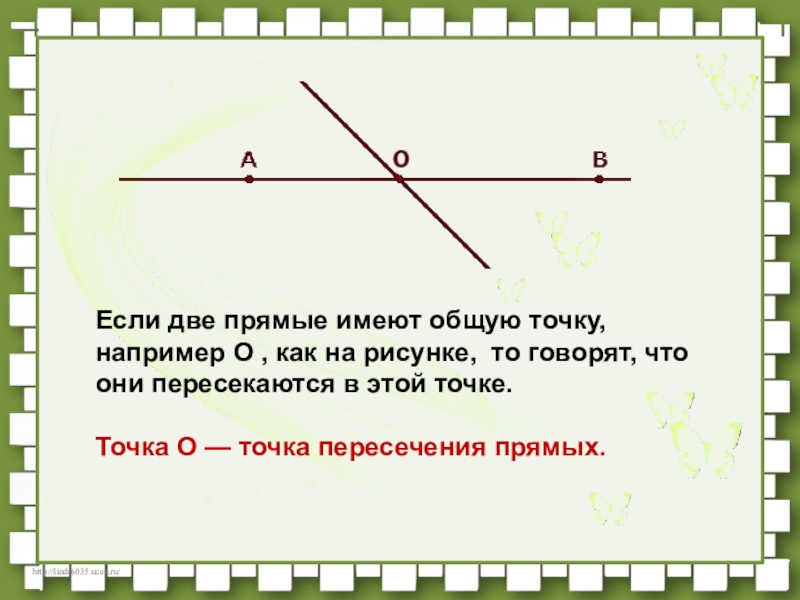
Слайд 5Если две прямые имеют общую точку, например O , как на рисунке, то говорят,
что они пересекаются в этой точке.
Точка O — точка пересечения прямых.
Точка O — точка пересечения прямых.
Слайд 6Н
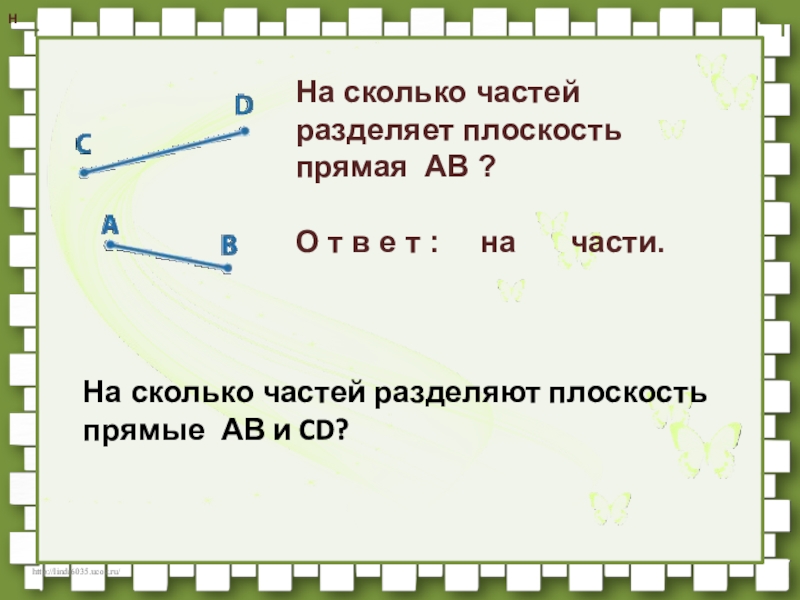
На сколько частей разделяет плоскость прямая AB ?
О
т в е т : на части.
На сколько частей разделяют плоскость
прямые AB и CD?
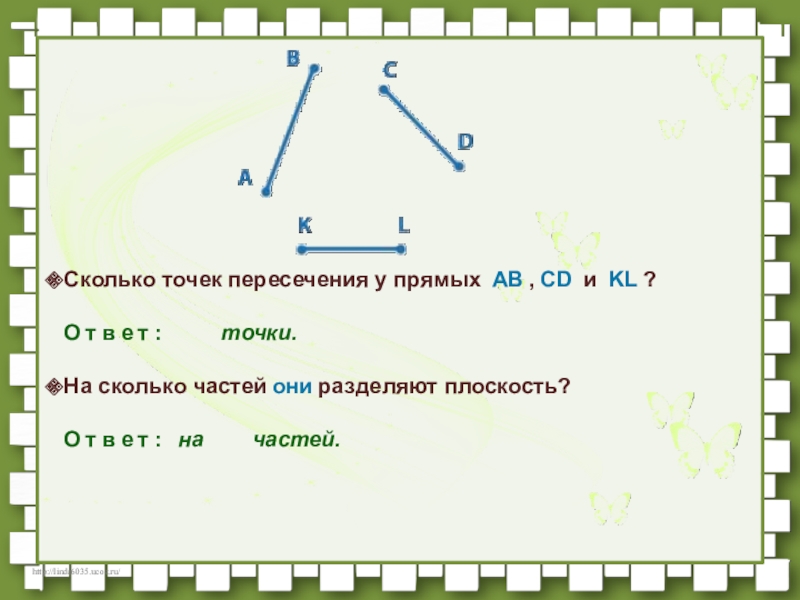
Слайд 7Сколько точек пересечения у прямых AB , CD и KL ? О т в е т :
точки.
На сколько частей они разделяют плоскость? О т в е т : на частей.
На сколько частей они разделяют плоскость? О т в е т : на частей.
Слайд 10Длины измеряют разными измерительными
приборами. Один из них — линейка
Деления, нанесенные на
линейку, разбивают ее на равные части.
Расстояние между мелкими рисками равно 1 миллиметр, а между крупными
1 сантиметр.
Расстояние между мелкими рисками равно 1 миллиметр, а между крупными
1 сантиметр.
Слайд 11Шкалы могут быть и на других измерительных приборах, например термометр. Данный термометр имеет
цену деления равную
1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).
1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).
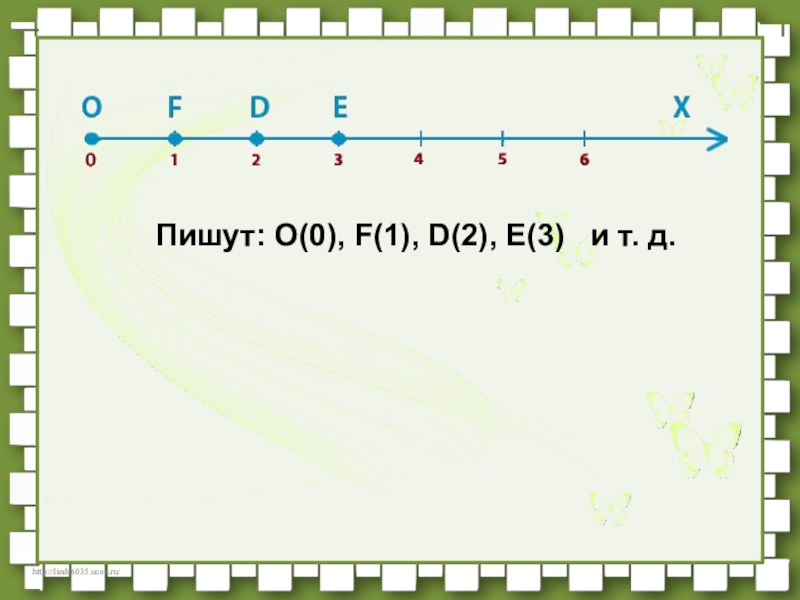
Слайд 12Нарисуем луч ОХ. Отметим на этом луче точку F.
Под началом луча, точка O , напишем число 0 ,
а под точкой F — число 1.
Отрезок OF называется единичным отрезком.
Нанесем на луч точку D , так чтобы расстояние OF было равно расстоянию FD и под точкой D напишем число 2 .
Затем на этом же луче отложим отрезок DE , равный единичному отрезку, и под точкой E напишем число 3 .
Отрезок OF называется единичным отрезком.
Нанесем на луч точку D , так чтобы расстояние OF было равно расстоянию FD и под точкой D напишем число 2 .
Затем на этом же луче отложим отрезок DE , равный единичному отрезку, и под точкой E напишем число 3 .
Повторяя эти действия, мы получим бесконечную шкалу.
Ее называют координатным лучом.
Слайд 141000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100
кг = 1 ц (центнер);
1000 кг = 1 т (тонна).
1000 кг = 1 т (тонна).
Слайд 18
Выразите в граммах:
1) 8 кг 300 г =
грамм ;
2) 4 кг 83 г = грамм ; 3) 3 кг 70 г = грамм ;
4) 11 кг 7 г = грамм .
2) 4 кг 83 г = грамм ; 3) 3 кг 70 г = грамм ;
4) 11 кг 7 г = грамм .
Слайд 19
Выразите в килограммах:
1) 4т 3ц
= килограмм ;
2) 5ц 8 кг = килограмм ; 3) 33т 7ц 3кг = килограмм ;
4) 11 ц 7 кг = килограмм .
2) 5ц 8 кг = килограмм ; 3) 33т 7ц 3кг = килограмм ;
4) 11 ц 7 кг = килограмм .
Слайд 21При счете натуральные числа называют по порядку: 1, 2, 3, 4, ... . Число,
которое при счете называют раньше, меньше того,
которое при счете называют позже.
Число 1 меньше, чем 3, а число 4 больше, чем 3.
Единица — самое маленькое натуральное число.
Точка с меньшей координатой лежит на координатном луче левее
точки с большей координатой.
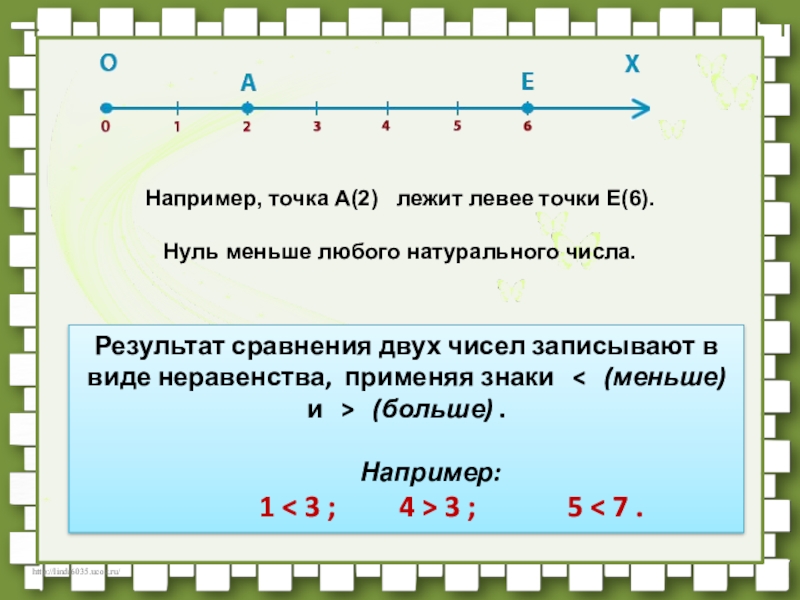
Слайд 22Например, точка A(2) лежит левее точки E(6).
Нуль меньше любого
натурального числа.
Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше) .
Например:
1 < 3 ; 4 > 3 ; 5 < 7 .
Слайд 23Число 3 меньше, чем 4, и больше, чем 1. Это записывают в виде
двойного неравенства:
1 < 3 < 4 .
Так как нуль меньше, чем единица, то записывают: 0 < 1 .
Так как нуль меньше, чем единица, то записывают: 0 < 1 .
Слайд 24 Многозначные числа сравнивают так.
Число 1007 больше, чем 929, потому что
1007 — четырехзначное число, а 929 —
трехзначное.
1007 > 929.
Числа 3221 и 1723 — четырехзначные, но
3221 > 1723, потому что в первом числе больше тысяч, чем во втором.
В четырехзначных числах 7505 и 7287 поровну тысяч, но сотен в первом числе больше, и потому
7505 > 7287 .
Числа 3221 и 1723 — четырехзначные, но
3221 > 1723, потому что в первом числе больше тысяч, чем во втором.
В четырехзначных числах 7505 и 7287 поровну тысяч, но сотен в первом числе больше, и потому
7505 > 7287 .
Слайд 25Меньшее число должно находиться с острого (маленького) конца знака, а большее с широкого (большого) конца знака:
1 < 3 ; 3 > 1.
Слайд 27Какая из точек А или В лежит правее на координатном луче: а) A(1) или В(7) ;
б) A(16) или В(10)
в) A(20) или В(21) ; г) A(9) или В(8)
д) A(11) или В(22)
е) A(29) или В(31) .
Слайд 28Какая из точек А или В лежит левее на координатном луче: а) A(28) или В(46) ;
б) A(57) или В(56) ;
в) A(17) или В(23) ; г) A(0) или В(1) ;
д) A(70) или В(59) ;
е) A(48) или В(38) .
Слайд 29Выберите пять самых маленьких чисел из десяти: 25 ; 63
; 34 ; 58 ; 49 ;
13 ; 38 ; 46 ; 12 ; 47 .
Слайд 30Выберите пять самых больших чисел из десяти: 37 ; 54
; 26 ; 49 ; 19 ;
52 ; 21 ; 31 ; 33 ; 25 .
