- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Пирамиды
Содержание
- 1. Презентация по математике на тему Пирамиды
- 2. Цели урокаПознакомится с историей пирамид, пирамиды вокруг
- 3. Из истории пирамидНачало геометрии пирамиды было положено
- 4. «Пирамида» - от греческого слова «пюрамис», которым
- 5. Слайд 5
- 6. Слайд 6
- 7. ПИРАМИДЫ В АРХИТЕКТУРЕНовый вход в Лувр, ПарижТорговый
- 8. Современные здания
- 9. Пирамида – это многогранник, у которого одна
- 10. Многоугольник A1A2…An называется основанием пирамиды, треугольники A1PA2
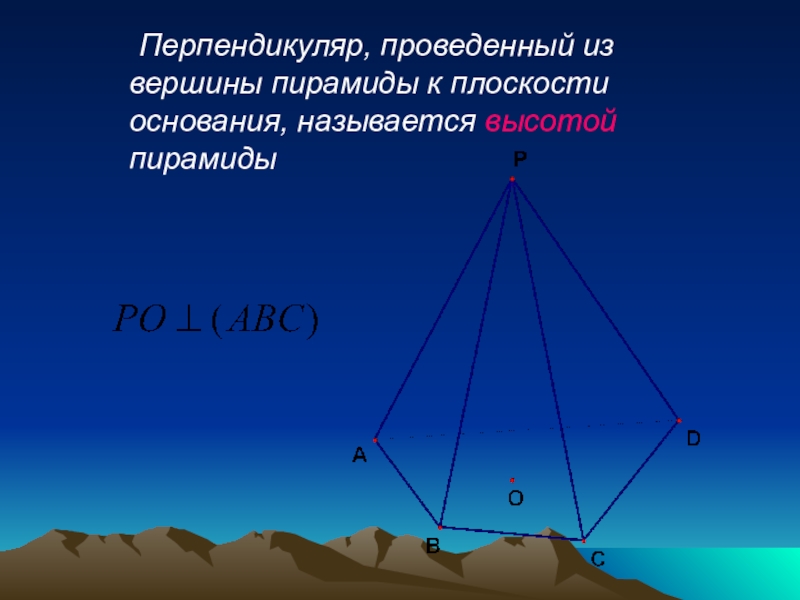
- 11. Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды
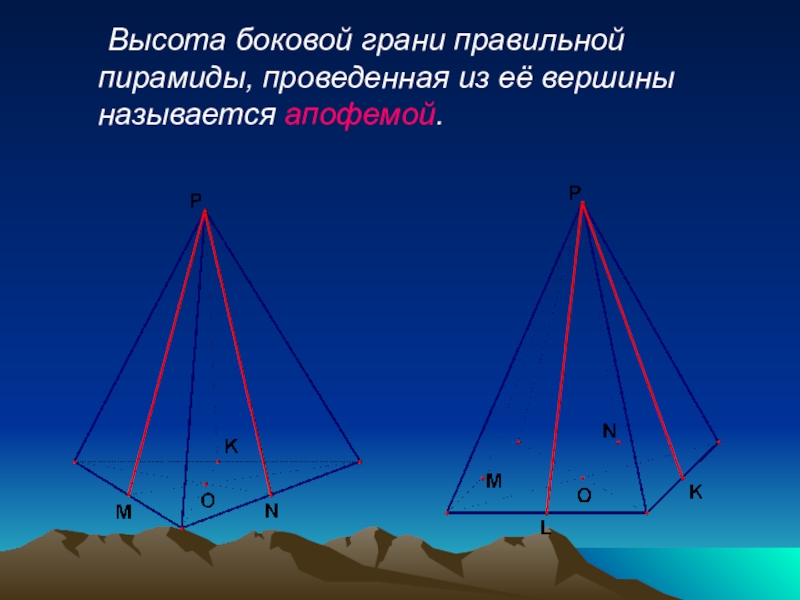
- 12. Высота боковой грани правильной пирамиды, проведенная из её вершины называется апофемой.
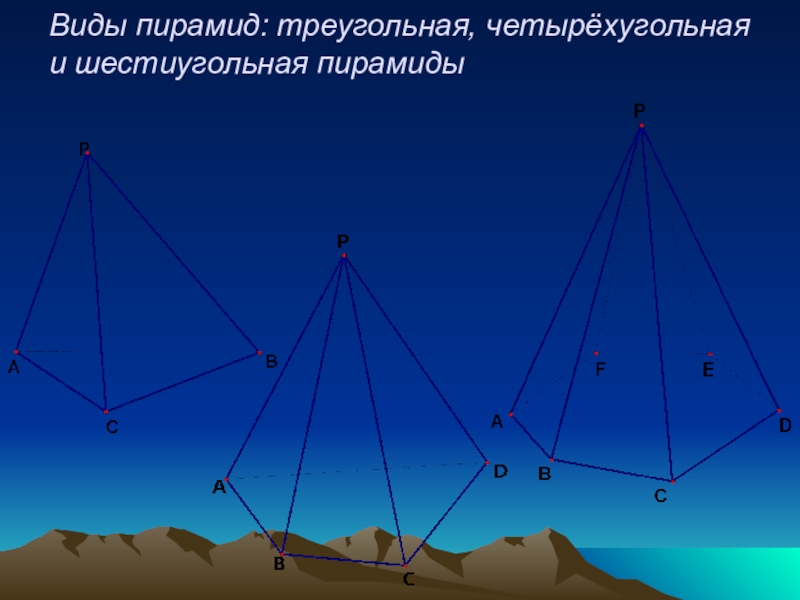
- 13. Виды пирамид: треугольная, четырёхугольная и шестиугольная пирамиды
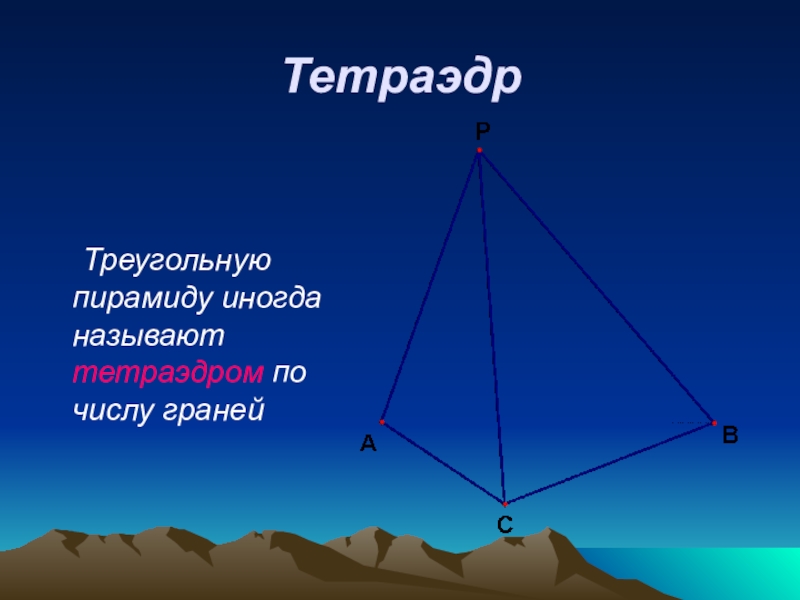
- 14. Тетраэдр Треугольную пирамиду иногда называют тетраэдром по числу граней
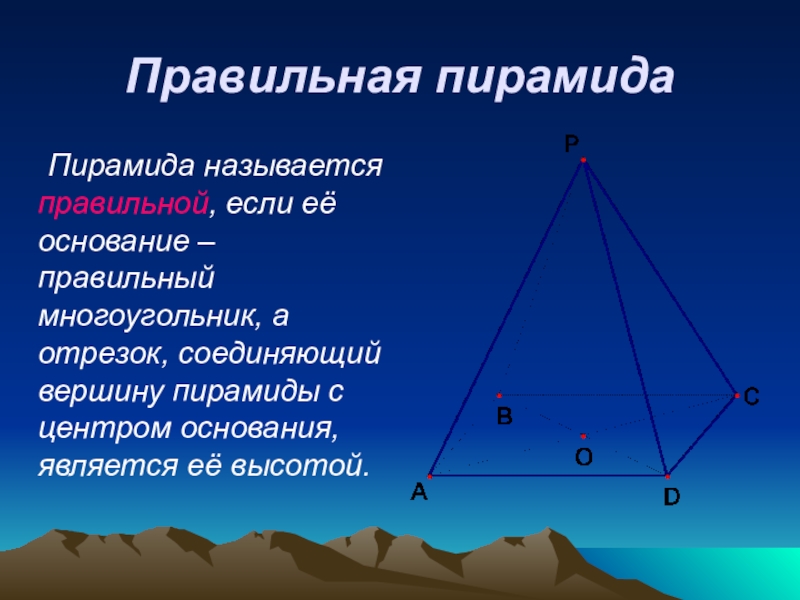
- 15. Правильная пирамида Пирамида называется правильной, если её основание
- 16. Правильные пирамиды
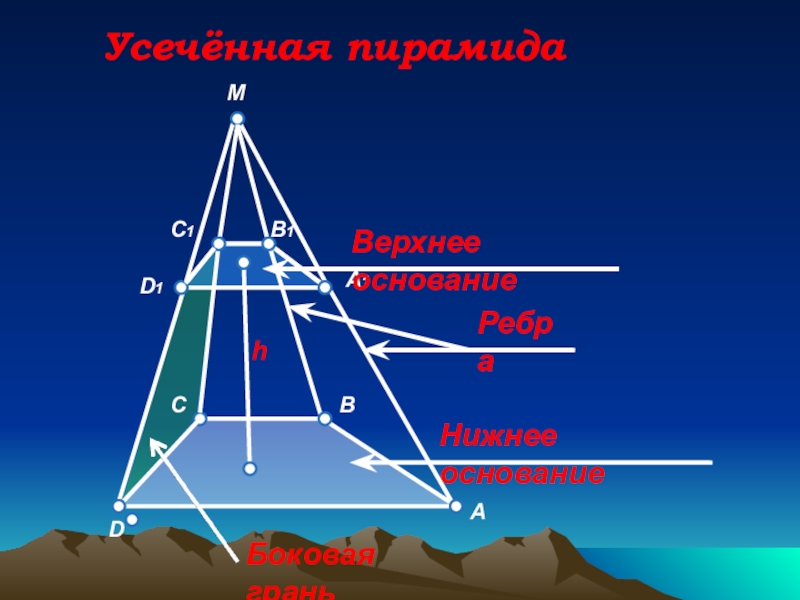
- 17. MCBD1DAC1A1B1Усечённая пирамидаВерхнее основаниеНижнее основаниеРебраБоковая граньh
- 18. Площадь поверхности пирамидыПлощадь полной поверхности пирамиды равна
- 19. Объем пирамидыОбъем пирамиды равен 1/3 произведения площади основания на высоту.Vпир. = 1/3 Sосн ⋅ h
- 20. Спасибо за внимание
Цели урокаПознакомится с историей пирамид, пирамиды вокруг нас.Изучить определение пирамиды, ее элементы.Изучить виды пирамид.Изучить формулы площади боковой и полной поверхности пирамиды, объема пирамиды.
Слайд 2Цели урока
Познакомится с историей пирамид, пирамиды вокруг нас.
Изучить определение пирамиды, ее
элементы.
Изучить виды пирамид.
Изучить формулы площади боковой и полной поверхности пирамиды, объема пирамиды.
Изучить виды пирамид.
Изучить формулы площади боковой и полной поверхности пирамиды, объема пирамиды.
Слайд 3Из истории пирамид
Начало геометрии пирамиды было положено в Древнем Египте и
Вавилоне, однако активное развитие получило в Древней Греции. Объем пирамиды был известен древним египтянам. Первым греческим математиком, кто установил, чему равен объём пирамиды, был Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке
Слайд 4«Пирамида» - от греческого
слова «пюрамис», которым
греки называли египетские
пирамиды.
Мексиканская
пирамида Солнца
Египетские пирамиды
Гора Кайлас на Тибете
Слайд 7ПИРАМИДЫ В АРХИТЕКТУРЕ
Новый вход в Лувр, Париж
Торговый центр в Илинге,
Лондон
Александрийский маяк
Слайд 9Пирамида – это многогранник, у которого одна грань ( основание пирамиды
) – это произвольный многоугольник ABCDE, а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды.
Слайд 10 Многоугольник A1A2…An называется основанием пирамиды,
треугольники A1PA2 , A2PA3 , …
, AnPA1 – боковыми гранями пирамиды.
Точка P называется вершиной пирамиды, а отрезки PA1, PA2, …,PAn - её боковыми ребрами.
Точка P называется вершиной пирамиды, а отрезки PA1, PA2, …,PAn - её боковыми ребрами.
Слайд 11 Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды
Слайд 15Правильная пирамида
Пирамида называется правильной, если её основание – правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
Слайд 18Площадь поверхности пирамиды
Площадь полной поверхности пирамиды равна сумме площадей основания и
боковой поверхности.
Sполн. = Sосн. + Sбок.
l
а
Слайд 19Объем пирамиды
Объем пирамиды равен 1/3 произведения площади основания на высоту.
Vпир. =
1/3 Sосн ⋅ h