- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Делимость натуральных чисел
Содержание
- 1. Презентация по математике на тему Делимость натуральных чисел
- 2. Делители и кратныеНатуральное число а делится нацело
- 3. Что означает: а, b – кратны
- 4. (a + b) кратна с(a + b)
- 5. Чётные и Нечётные числаНазовите все четные цифры
- 6. Чётные и нечётные натуральные числаКакие натуральные числа
- 7. Признак делимости на 2На 2 делятся все
- 8. Признак делимости на 5На 5 делятся все
- 9. Признак делимости на 10На 10 делятся все
- 10. Признак делимости на 3На 3 делятся все
- 11. Признак делимости на 9На 9 делятся все
- 12. Простые и составные числаНатуральное число называется простым,
- 13. НОДНаибольшее натуральное число, на которое делится нацело
- 14. НОКНаименьшее натуральное число, которое делится нацело на
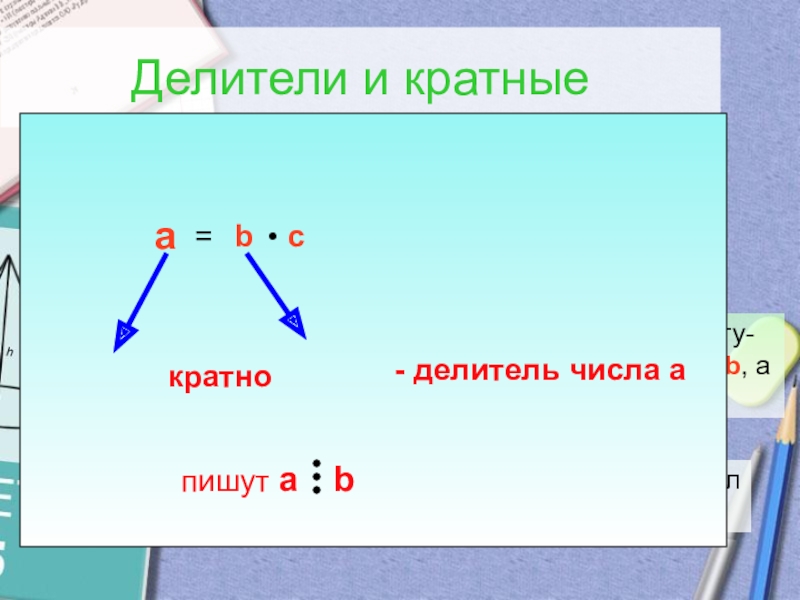
Слайд 2Делители и кратные
Натуральное число а делится нацело на натуральное число b,
а
=
b
•
с
Если натуральное число а делится нацело на нату-ральное число b, то число а называют кратным b, а число b – делителем числа а.
Для любого натурального числа а каждое из чисел
а•1, а•2,а•3, а•4, … является кратным числа а.
=
b
с
a
•
кратно
- делитель числа а
пишут а b
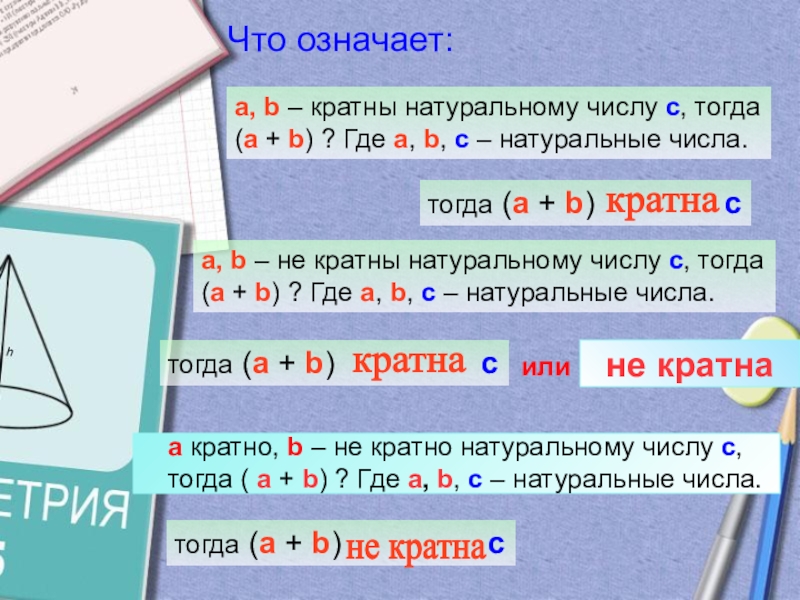
Слайд 3Что означает:
а, b – кратны натуральному числу с, тогда
(a
тогда (а + b) с
кратна
а, b – не кратны натуральному числу с, тогда
(a + b) ? Где а, b, с – натуральные числа.
тогда (а + b) с
кратна
не кратна
или
а кратно, b – не кратно натуральному числу с,
тогда ( а + b) ? Где а, b, с – натуральные числа.
тогда (а + b) с
не кратна
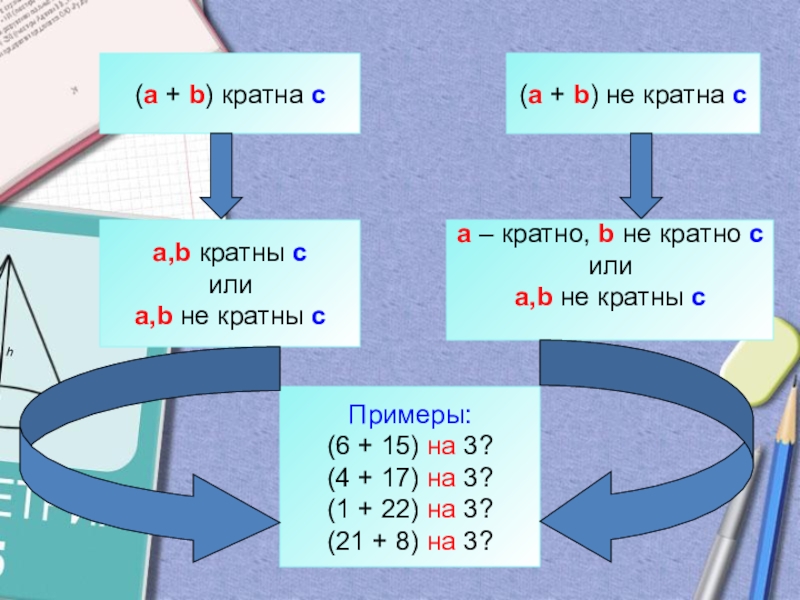
Слайд 4(a + b) кратна с
(a + b) не кратна с
а,b кратны
или
а,b не кратны с
а – кратно, b не кратно с
или
а,b не кратны с
Примеры:
(6 + 15) на 3?
(4 + 17) на 3?
(1 + 22) на 3?
(21 + 8) на 3?
Слайд 5Чётные и Нечётные числа
Назовите все четные цифры которыми записывается натуральное число?
Назовите
0
1
2
3
4
5
6
7
8
9
1
3
5
1
3
7
5
1
3
9
7
5
1
3
1
2
1
3
2
1
4
3
2
1
5
4
3
2
1
6
5
4
3
2
1
7
6
5
4
3
2
1
8
7
6
5
4
3
2
1
9
8
7
6
5
4
3
2
1
0
2
4
0
2
6
4
0
2
8
6
4
0
2
3
1
5
3
1
7
5
3
1
9
7
5
3
1
Слайд 6Чётные и нечётные натуральные числа
Какие натуральные числа называются чётными?
Все
Какие натуральные числа называются нечётными?
Все числа запись которых оканчивается нечётной цифрой (1,3,5,7,9) - нечётные числа.
Слайд 7Признак делимости на 2
На 2 делятся все натуральные числа, последняя цифра
17 358
:
2
8 : 2
17 358 : 2 = 8 679
так как
Слайд 8Признак делимости на 5
На 5 делятся все натуральные числа, последняя цифра
31 785 : 5
563 420 : 5
так как
5 : 5
0 : 5
31 785 : 5 = 6 357
563 420 : 5 = 112 684
Слайд 9Признак делимости на 10
На 10 делятся все натуральные числа, последняя цифра
на 100 последняя цифра которых оканчивается 00
на 1000 последняя цифра которых оканчивается 000 и т.д.
5 627 320 : 10
так как
0 : 10
5 627 320 : 10 = 562 732
Что можно сказать о числе 5 627 320?
5 627 320 ещё делится на ...
5
2
Если натуральное число делится на 10,
то одновременно это число делится и на 5 и на 2.
5 627 320 : 10 = 562 732
5 627 320 : 5 = 1 125 464
5 627 320 : 2 = 2 813 660
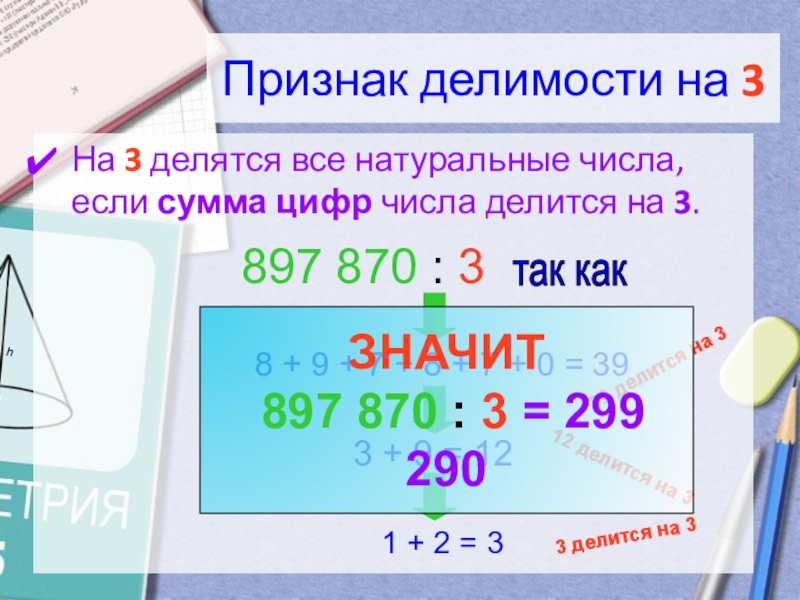
Слайд 10Признак делимости на 3
На 3 делятся все натуральные числа, если сумма
897 870 : 3
так как
8 + 9 + 7 + 8 + 7 + 0 = 39
3 + 9 = 12
1 + 2 = 3
39 делится на 3
12 делится на 3
3 делится на 3
ЗНАЧИТ
897 870 : 3 = 299 290
Слайд 11Признак делимости на 9
На 9 делятся все натуральные числа, если сумма
5 472 081 : 9
5 + 4 + 7 + 2 + 0 + 8 + 1 = 27
2 + 7 = 9
27 делится на 9
9 делится на 9
ЗНАЧИТ
5 472 081 : 9 = 608 009
так как
Слайд 12Простые и составные числа
Натуральное число называется простым, если оно имеет только
Натуральное число называется составным, если оно имеет более двух натуральных делителей.
а = 1 • а, где а – простое натуральное число
a = b • c • … • a, где а – составное натуральное число
Слайд 13НОД
Наибольшее натуральное число, на которое делится нацело каждое из двух данных
Если натуральное число а – делитель числа b, то НОД (а;b) = а
НОД (а;b) = с, где а, b кратно с
а, b, с – натуральные числа
НОД (а;b) = а, где а - делитель b
а, b – натуральные числа
Если НОД двух натуральных чисел равен 1, то числа
называют взаимно простыми.
НОД (а;b) = 1, где а,b – натуральные числа
Любые два простых числа, являются взаимно простыми.
НОД (13;23) = 1
Слайд 14НОК
Наименьшее натуральное число, которое делится нацело на каждое из двух данных
Если число а –делитель числа b, то наименьшее общее кратное чисел равно b.
НОК (a;b) = с , где с кратно а и b
a, b, c – натуральные числа
НОК (a;b) = b , где b кратно а
a, b – натуральные числа
Наименьшее общее кратное взаимно простых
чисел равно их произведению.
НОК (а;b) = a • b, где НОД (а;b) = 1
а, b – натуральные числа
НОК (а;b) • НОД (а;b) = a • b,
где а, b – натуральные числа