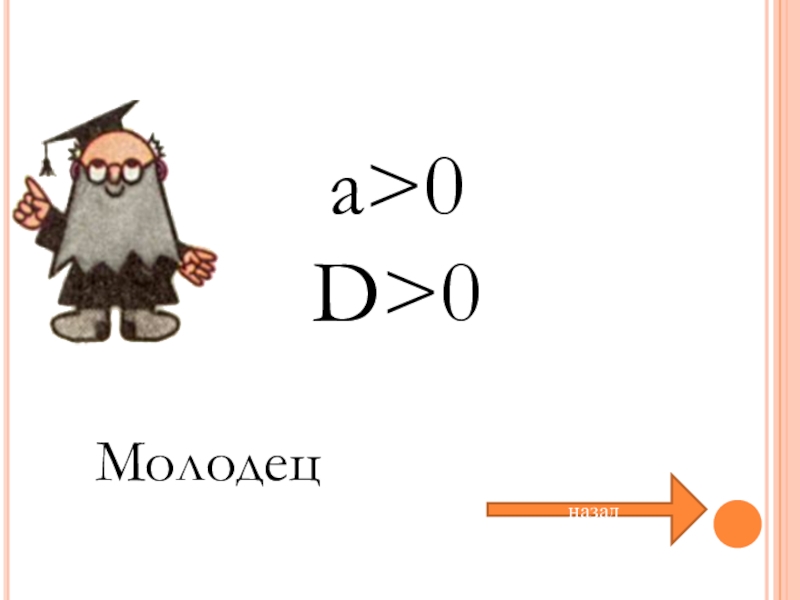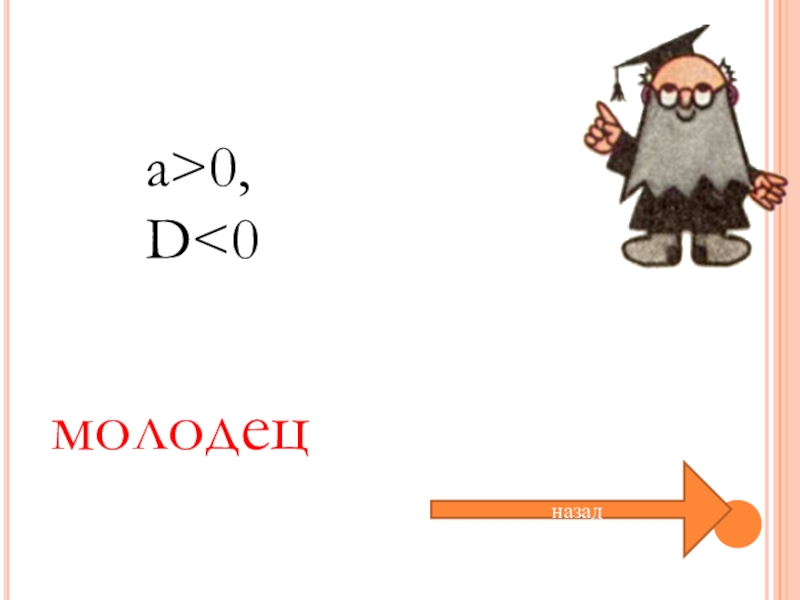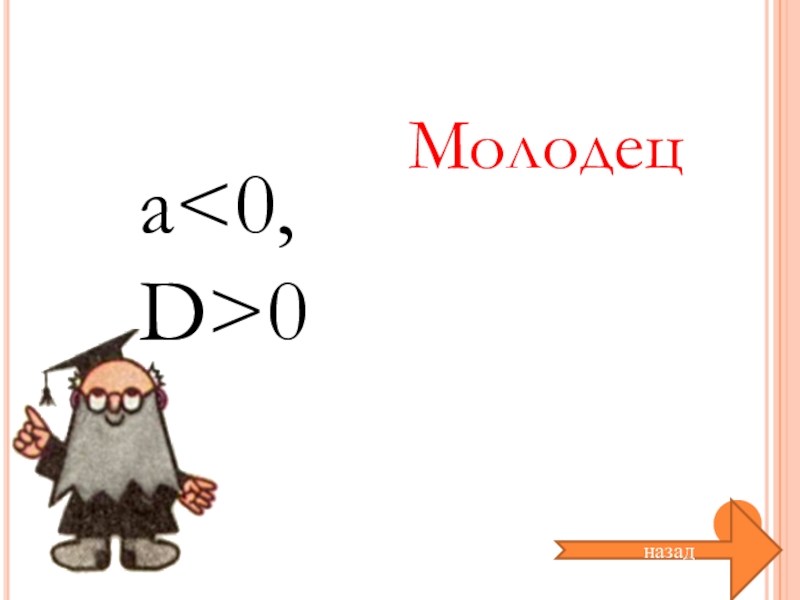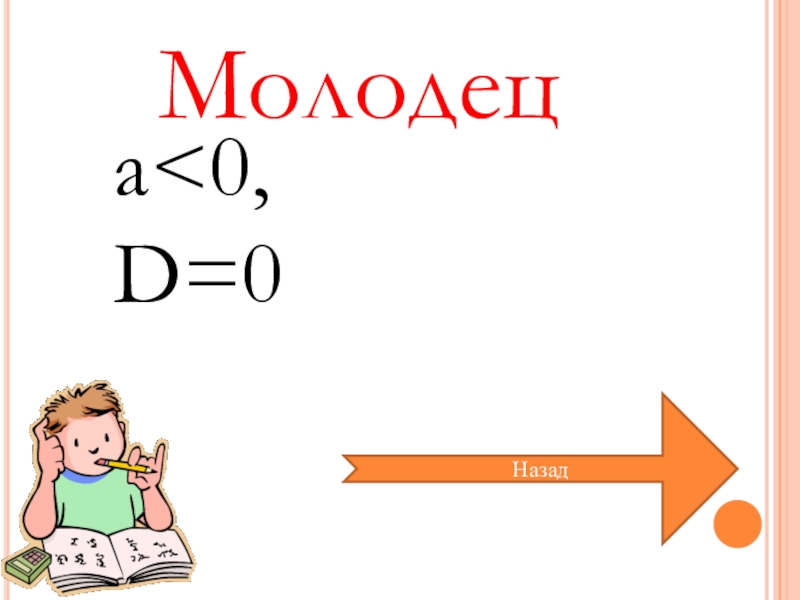- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему
Содержание
- 1. Презентация по математике на тему
- 2. абвгде 1. Используя график функции y=ax
- 3. Понятиеквадратных неравенствРешение квадратных неравенствК содержанию
- 4. Квадратные неравенства Неравенства вида f(x)>0, f(x)0 или ax2+bx+c
- 5. Если D0, при a>0 являются все действительные числа, а
- 6. 1) Рассмотрим квадратичную функцию f(x) = x2
- 7. 4) Изобразим схематично параболу f(x) = x2
- 8. Рассмотрим решение квадратных неравенств на конкретном примере.Решим неравенство x2-5x-50
- 9. Тест Данный тест поможет правильно оценить Ваши
- 10. 1. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .x2–6x–70≥0Да.Нет.
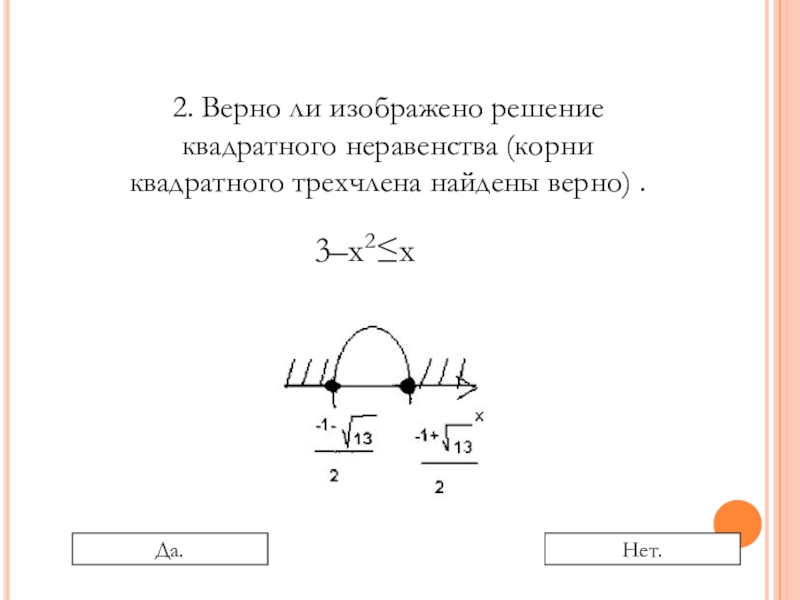
- 11. 2. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3–х2≤х Да.Нет.
- 12. 2. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3–х2≤х Да.Нет.
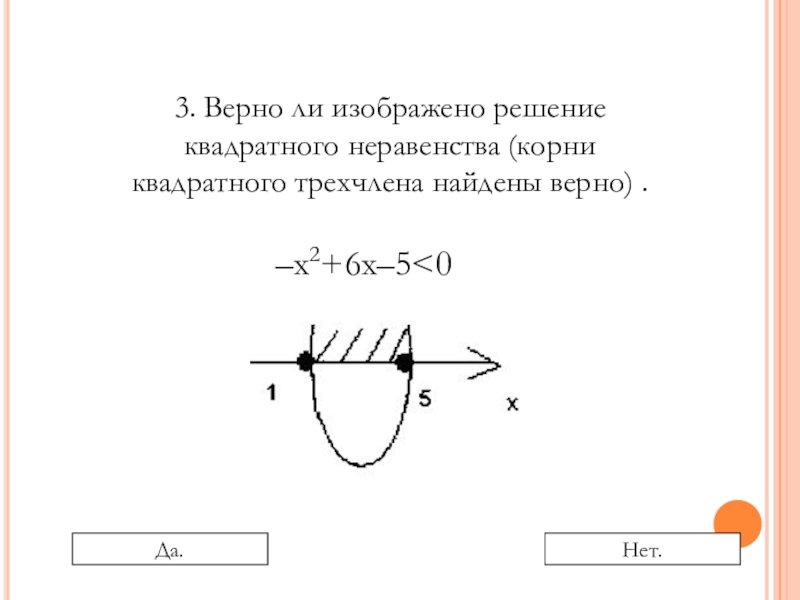
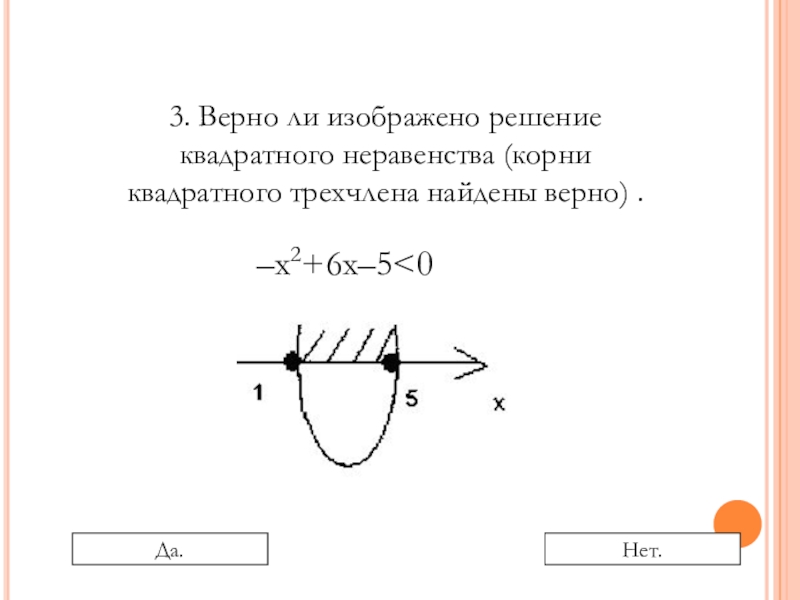
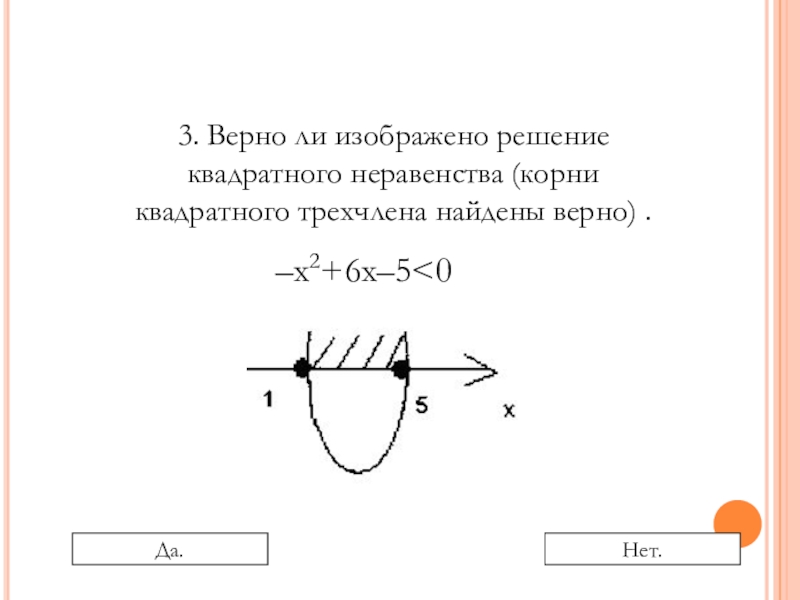
- 13. –х2+6х–5
- 14. –х2+6х–5
- 15. –х2+6х–5
- 16. 4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .х2-3х+2≤0Да.Нет.
- 17. 4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .х2-3х+2≤0Да.Нет.
- 18. 4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .х2-3х+2≤0Да.Нет.
- 19. 4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .х2-3х+2≤0Да.Нет.
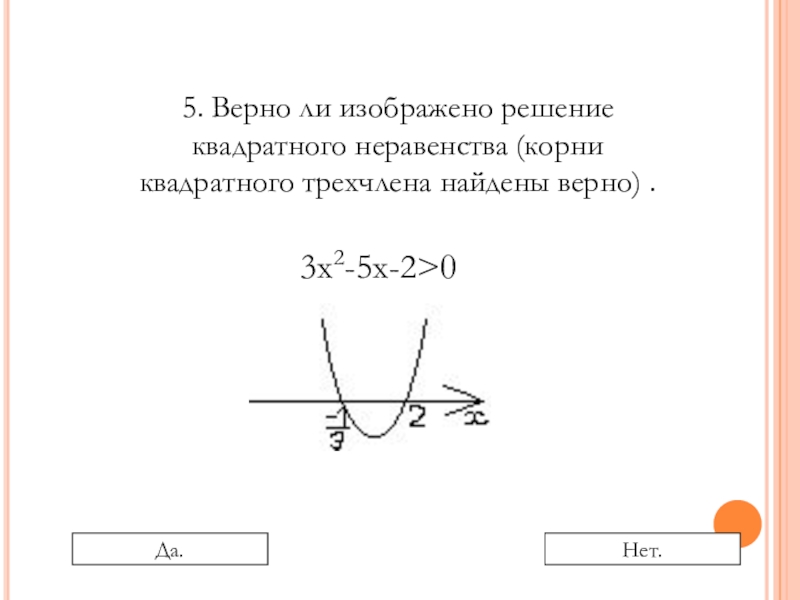
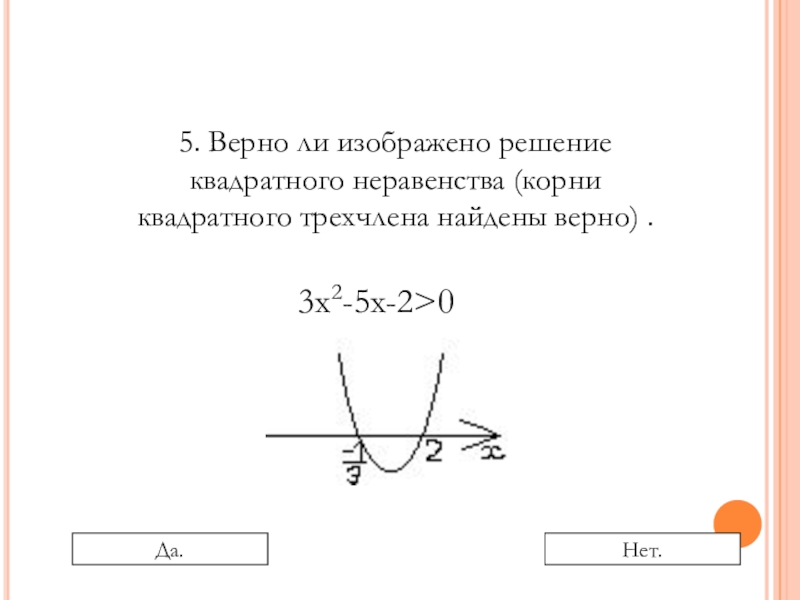
- 20. 5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3х2-5х-2>0Да.Нет.
- 21. 5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3х2-5х-2>0Да.Нет.
- 22. 5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3х2-5х-2>0Да.Нет.
- 23. 5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3х2-5х-2>0Да.Нет.
- 24. 5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) .3х2-5х-2>0Да.Нет.
- 25. 5 К содержанию
- 26. К содержанию4
- 27. К содержанию3
- 28. К содержанию2
- 29. К содержанию1
- 30. К содержанию0
- 31. а>0D>0назадМолодец
- 32. a>0,D
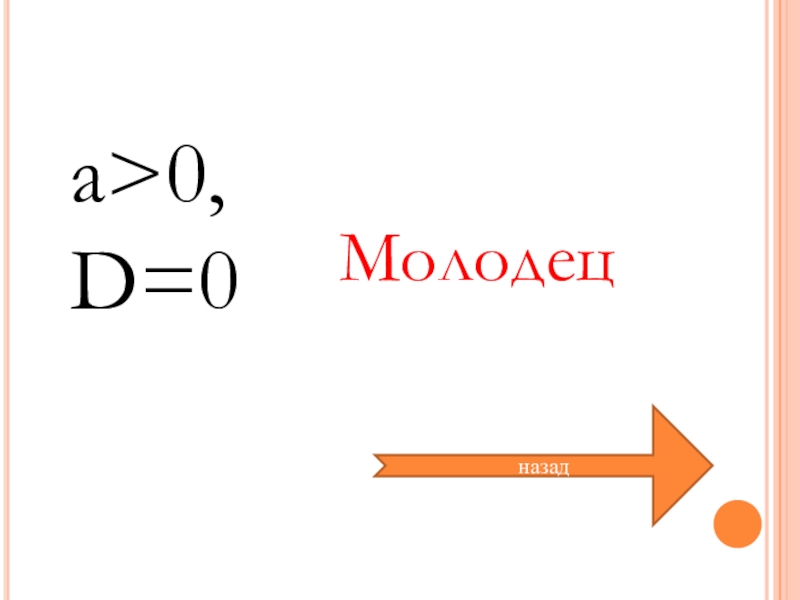
- 33. a>0,D=0Молодецназад
- 34. назадa0Молодец
- 35. a
- 36. a
абвгде 1. Используя график функции y=ax 2+bx+c:а. Охарактеризуйте знак первого коэффициента а и дискриминанта;б. Назовите значения переменной x , при которых функция принимает значения, равные нулю, положительные значения, отрицательные
Слайд 2а
б
в
г
д
е
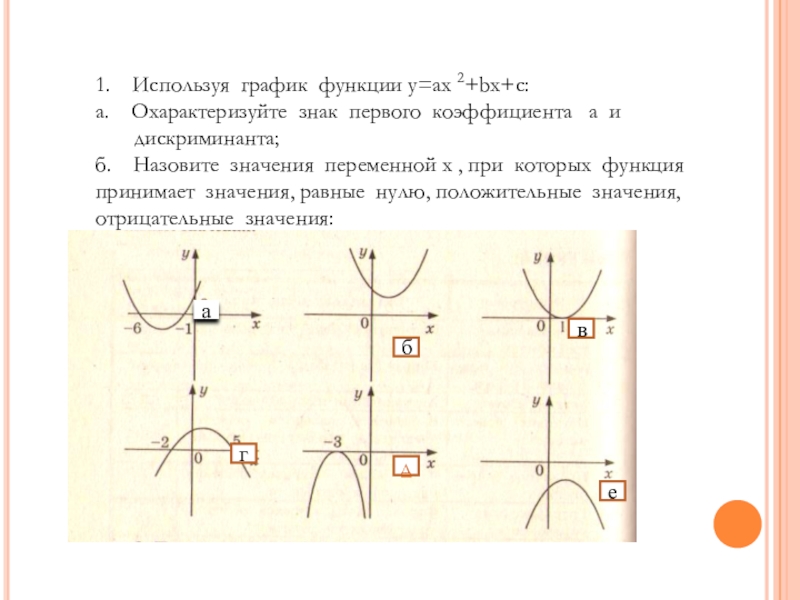
1. Используя график функции y=ax 2+bx+c:
а. Охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б. Назовите значения переменной x , при которых функция принимает значения, равные нулю, положительные значения, отрицательные значения:
дискриминанта;
б. Назовите значения переменной x , при которых функция принимает значения, равные нулю, положительные значения, отрицательные значения:
Слайд 4Квадратные неравенства
Неравенства вида f(x)>0, f(x)
или неравенствами второй степени, причем первые два из этих неравенств называют строгими, другие - нестрогими .
Перейдем к нахождению решений квадратных неравенств следующих видов: ax2+bx+c>0 или ax2+bx+c<0.
Перейдем к нахождению решений квадратных неравенств следующих видов: ax2+bx+c>0 или ax2+bx+c<0.
Далее
Слайд 5Если D0, при a>0 являются все действительные числа, а
неравенство ax2+bx+c<0, при a>0 не имеет решений;
Если D=0, то решениями неравенства ax2+bx+c>0 , являются все
действительные значения x, кроме
Если D=0, то решениями неравенства ax2+bx+c>0 , являются все
действительные значения x, кроме
а неравенство ax2+bx+c<0 не имеет решений;
Если D>0, то решениями неравенства ax2+bx+c>0 при a>0 являются все числа x , лежащие вне отрезка [x1, x2] .
А решениями неравенства ax2+bx+c<0 являются числа x из интервала (x1, x2).
К содержанию
К квадратным неравенствам
Слайд 61) Рассмотрим квадратичную функцию f(x) = x2 – 5 x -
50 и
найдем такие значения x, для которых f(x) < 0.
2) Графиком рассматриваемой функции является парабола,
ветви которой направлены вверх, так как a = 1, 1 > 0.
3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox), для этого решим квадратное уравнение
x2 – 5 x – 50 = 0.
D = 225 = 152, 225 > 0, значит уравнение имеет два действительных корня.
x1 = -5;
x2 = 10.
Нули функции: x = -5 и x = 10.
найдем такие значения x, для которых f(x) < 0.
2) Графиком рассматриваемой функции является парабола,
ветви которой направлены вверх, так как a = 1, 1 > 0.
3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox), для этого решим квадратное уравнение
x2 – 5 x – 50 = 0.
D = 225 = 152, 225 > 0, значит уравнение имеет два действительных корня.
x1 = -5;
x2 = 10.
Нули функции: x = -5 и x = 10.
Далее
Метод рассмотрения квадратичной функции
Слайд 74) Изобразим схематично параболу f(x) = x2 – 5x –50 в
координатной плоскости Oxy.
5) Из рисунка видим, что
f(x) < 0, при –5 < x < 10
(то есть берем в рассмотрение
ту часть параболы, которая
лежит ниже оси Ox).
Замечание: ответ записываем
в виде числового промежутка.
Ответ: (-5; 10).
К содержанию
Слайд 8Рассмотрим решение квадратных
неравенств на конкретном примере.
Решим неравенство x2-5x-50
квадратичной функции
Слайд 9Тест
Данный тест поможет правильно оценить Ваши знания.
При выполнении задания
Вам необходимо выбрать правильный вариант ответа. За каждый верный ответ зачисляется 1 баллов.
Максимальное количество баллов 5.
Для начала выполнения теста нажмите кнопку далее.
Желаю успеха!
Максимальное количество баллов 5.
Для начала выполнения теста нажмите кнопку далее.
Желаю успеха!
Далее
К содержанию
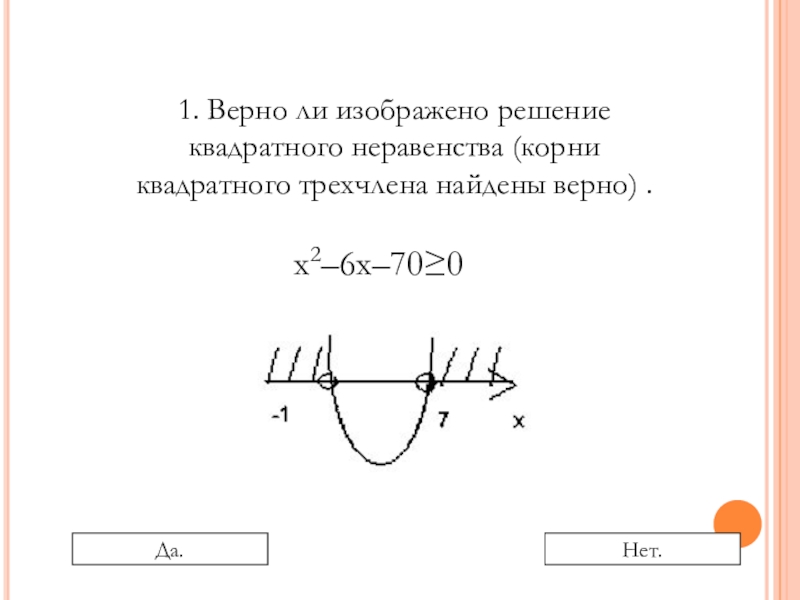
Слайд 101. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
x2–6x–70≥0
Да.
Нет.
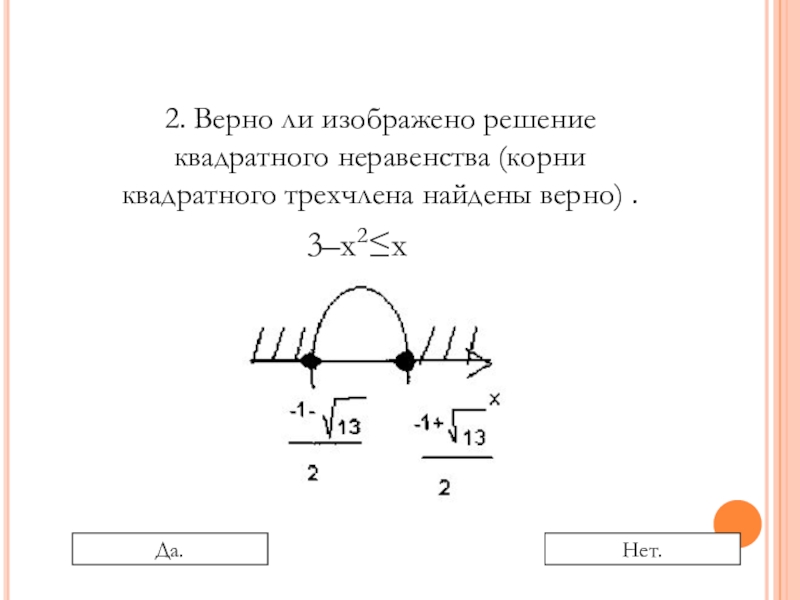
Слайд 112. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3–х2≤х
Да.
Нет.
Слайд 122. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3–х2≤х
Да.
Нет.
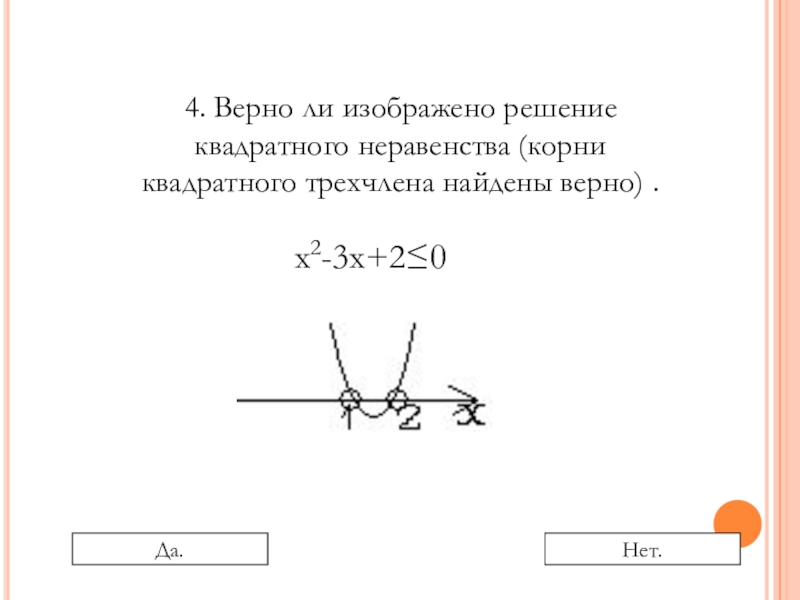
Слайд 164. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
х2-3х+2≤0
Да.
Нет.
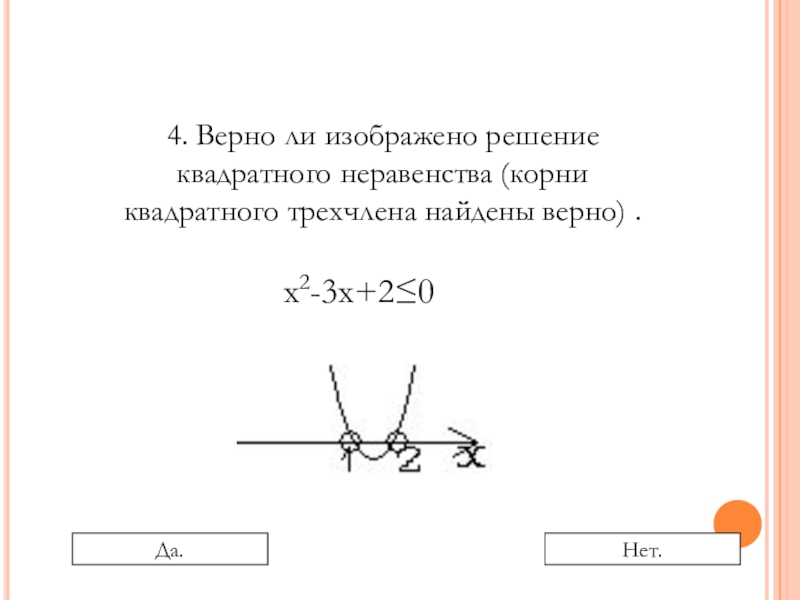
Слайд 174. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
х2-3х+2≤0
Да.
Нет.
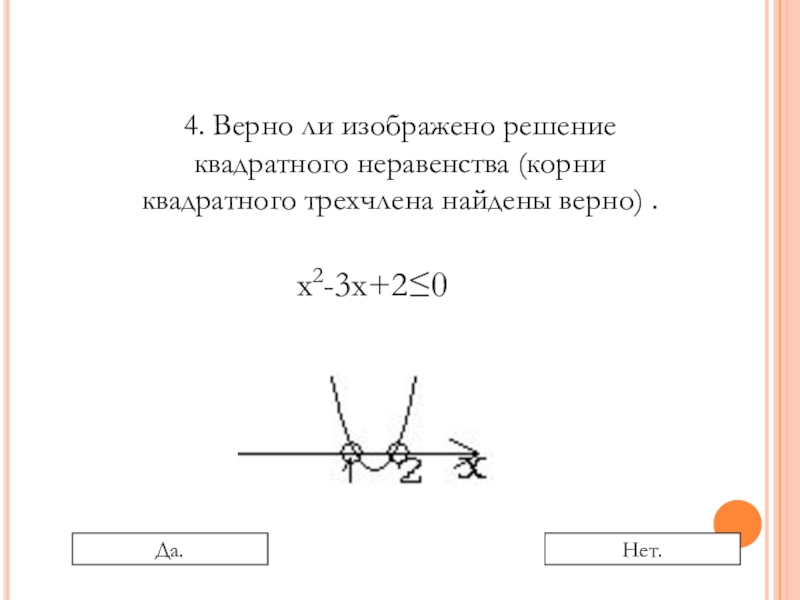
Слайд 184. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
х2-3х+2≤0
Да.
Нет.
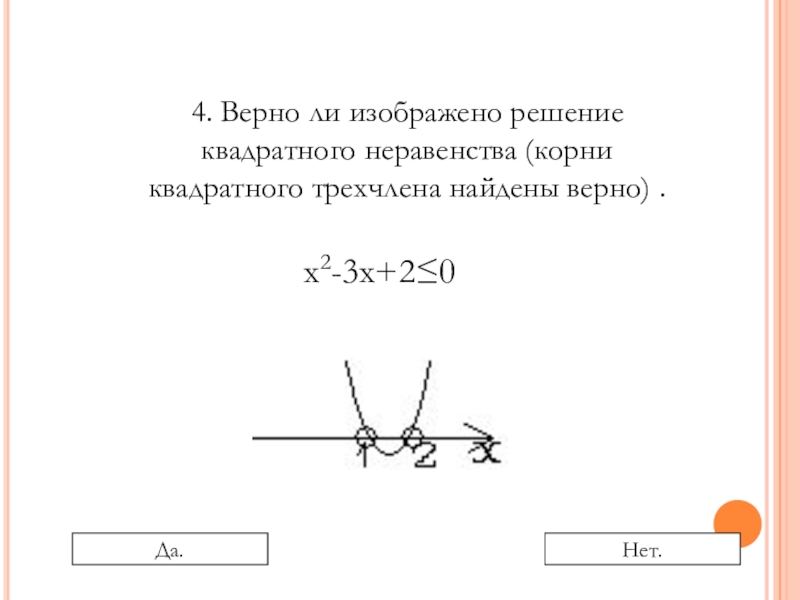
Слайд 194. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
х2-3х+2≤0
Да.
Нет.
Слайд 205. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3х2-5х-2>0
Да.
Нет.
Слайд 215. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3х2-5х-2>0
Да.
Нет.
Слайд 225. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3х2-5х-2>0
Да.
Нет.
Слайд 235. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3х2-5х-2>0
Да.
Нет.
Слайд 245. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены
верно) .
3х2-5х-2>0
Да.
Нет.
