- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему
Содержание
- 1. Презентация по математике на тему
- 2. Цели урока:Формирование представления о числовой последовательности как
- 3. Выполнить действия
- 4. Повторение видов функций. Укажите название , область
- 5. На одном из рисунков
- 6. На одном из рисунков
- 7. На одном из рисунков
- 8. На одном из рисунков изображена гипербола.Укажите номер этого рисунка. Задание 17(№ 193098)1234
- 9. Слайд 9
- 10. «Числа управляют миром»,- говорили древнегреческие ученые. «Все
- 11. Так первым четырем числам – 1, 2,
- 12. Сумма этих чисел – число 10 – изображало весь мир.
- 13. Прочитав высказывания, выдели главную мысль: Тот, кто
- 14. Проверь свою память2,4,6,8,10,12,14,16…….3,9,27,81,243…….1,1/2,1/3,1/4,1/5,1/6…..
- 15. Решите задачу: Некий фермер стал разводить кроликов,
- 16. 1, 1, 2, 3, 5, 8, 13,
- 17. ОпределениеПоследовательность, бесконечный,упорядоченный набор чисел (словарьС.И.Ожегова)Совокупность элементов
- 18. Числовая последовательностьЭто частный случай функции.Функция заданная на
- 19. Термины и символы:Числа образующие последовательность , называются
- 20. Чтобы задать последовательность, нужно указать способ, позволяющий
- 21. Указывается формула n-го члена последовательности.Пример. Последовательность квадратов
- 22. Правило составления последовательности выражается словесным описанием.Примеры.1) Последовательность
- 23. Указывается правило позволяющее вычислить n-й член данной
- 24. Свойства числовой последовательности.Обладает такими же свойствами ,какФункция: убывающая у1> у2> у3……..возрастающая у1< у2 < у3, КонечнаяБесконечнаяОграниченная
- 25. Решение задачВыпишите первые несколько членов последовательности натуральных
- 26. Самостоятельная работа:Последовательность (bn) задана
- 27. Рефлексия деятельности - Что узнали нового?Как можно
- 28. Слайд 28
- 29. http://pedsovet.su/ Для шаблона использованы источники:www.artgalery.ru/?id=300&ir=1&sm=95 mozeltexl.narod2.ru/google-1269.htm
Слайд 2Цели урока:
Формирование представления о числовой последовательности как функции с натуральным аргументом.
Формирование
Развитие умений применять ранее изученный материал.
Развитие умений анализировать, сравнивать, обобщать.
Привитие интереса к математике
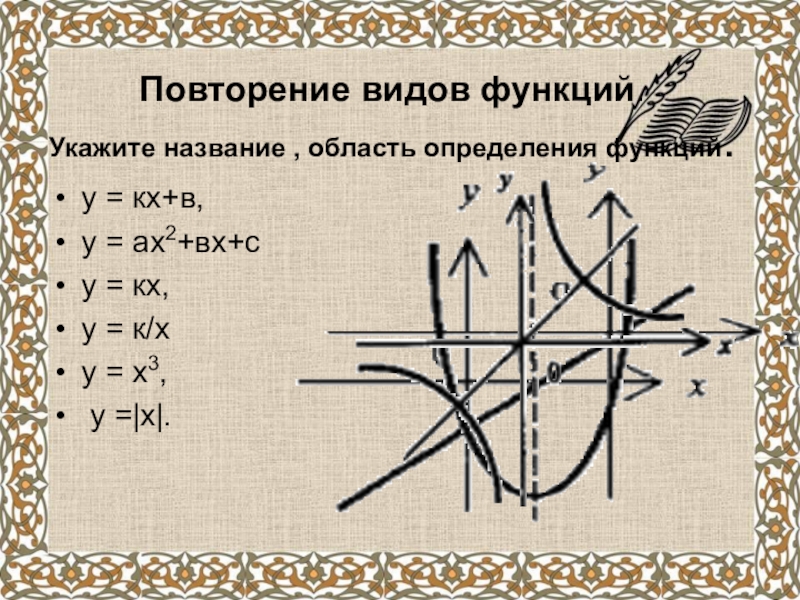
Слайд 4Повторение видов функций.
Укажите название , область определения функций.
у = кх+в,
у =
у = кх,
у = к/х
у = х3,
у =|х|.
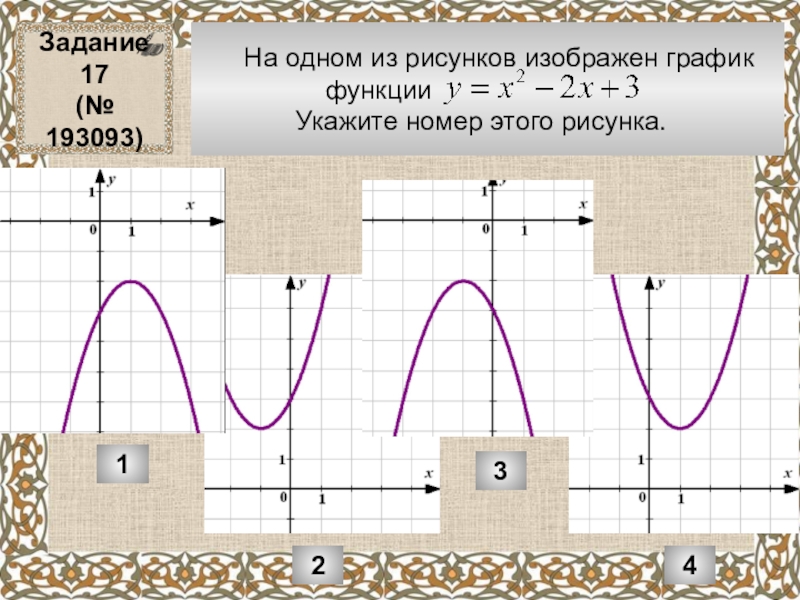
Слайд 5 На одном из рисунков изображен график
Укажите номер этого рисунка.
Задание 17
(№ 193093)
1
2
4
3
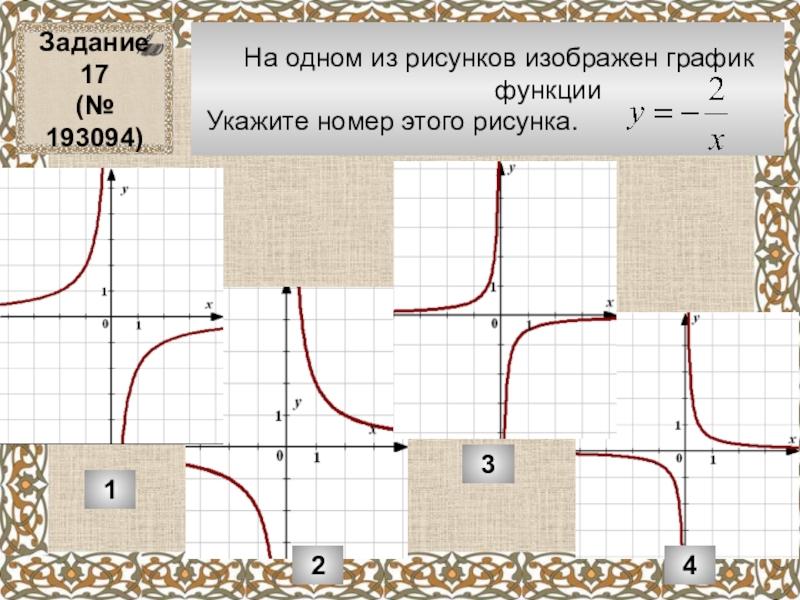
Слайд 6 На одном из рисунков изображен график
Укажите номер этого рисунка.
Задание 17
(№ 193094)
1
2
3
4
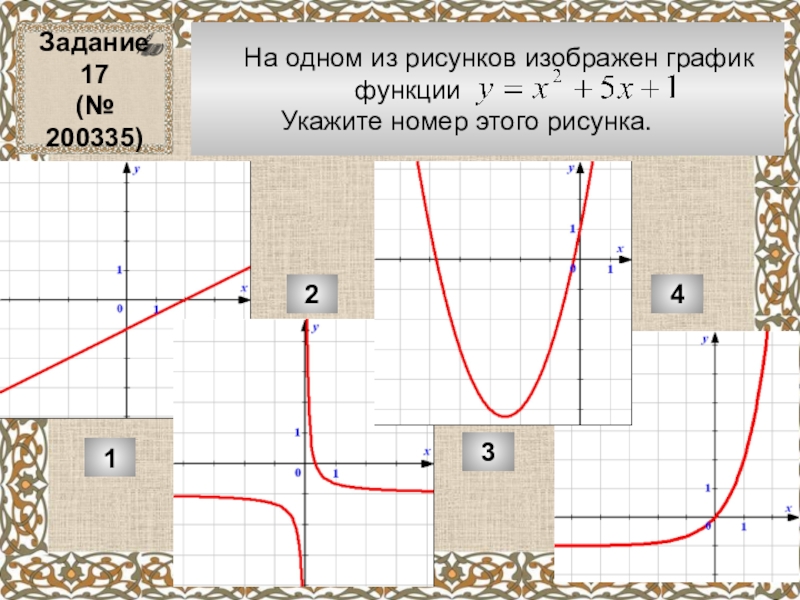
Слайд 7 На одном из рисунков изображен график
Укажите номер этого рисунка.
Задание 17
(№ 200335)
1
2
3
4
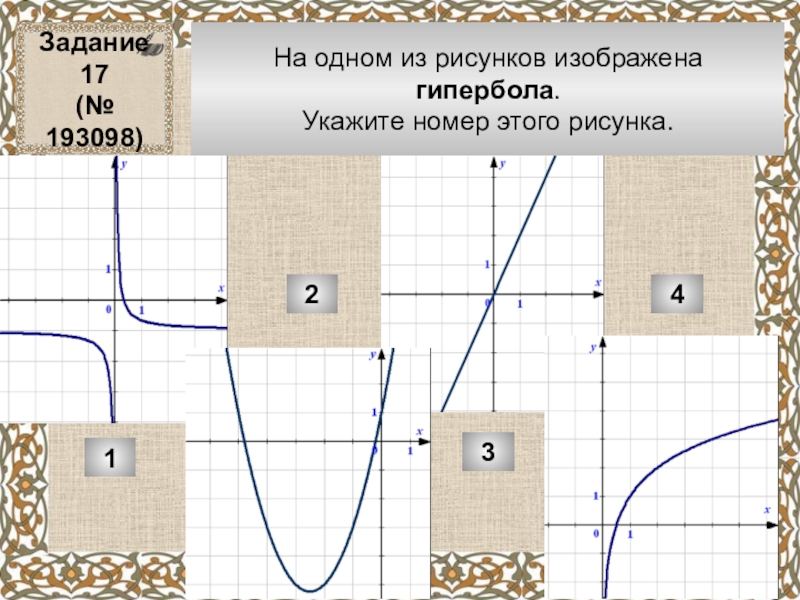
Слайд 8На одном из рисунков изображена
гипербола.
Укажите номер этого рисунка.
Задание 17
(№
1
2
3
4
Слайд 10«Числа управляют миром»,- говорили древнегреческие ученые. «Все есть число». Согласно их
Слайд 11Так первым четырем числам – 1, 2, 3, 4 – приписывалось:
1 – означает огонь
2 – землю
3 – воду
4 – воздух
Слайд 13Прочитав высказывания, выдели главную мысль:
Тот, кто мало знает, малому может и
Кто много говорит, тот мало делает.
Кто много болтает, тот много врет.
Кому многое дано, с того многое и взыщется!
У кого речь слаще, у того и благожелателей больше
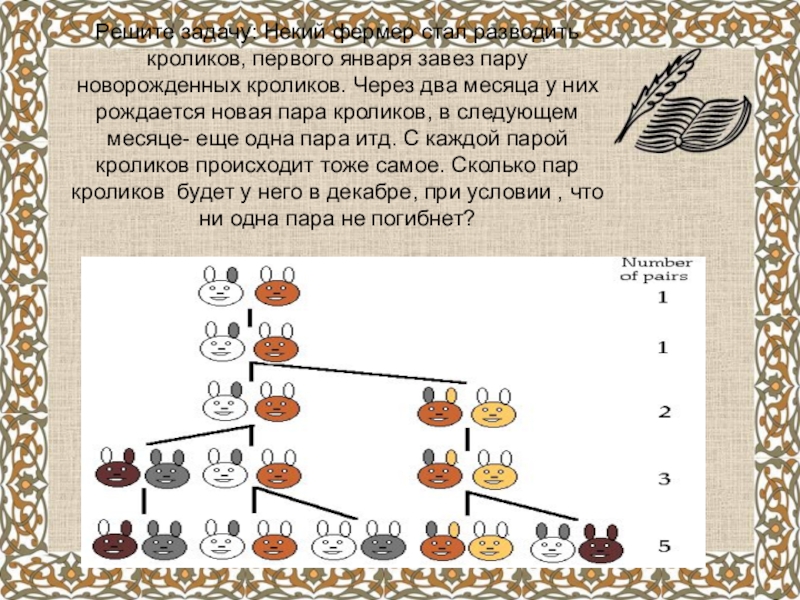
Слайд 15Решите задачу: Некий фермер стал разводить кроликов, первого января завез пару
Слайд 16
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
u1 = 1, u2 = 1, un+1 = un + un-1, n>2
Эту числовую последовательность называют последовательностью Фибоначчи по имени великого итальянского математика Леонардо Пизанского (Фибоначчи), который впервые описал решение задачи о кроликах в своем труде «Книга абака», опубликованном в 1202 г. Числа Фибоначчи нередко встречаются в природе (спирали роста у многих растений).
Слайд 17Определение
Последовательность, бесконечный,
упорядоченный набор чисел (словарьС.И.Ожегова)
Совокупность элементов любой природы, занумерованных натуральными
Числовая последовательность — это последовательность элементов числового пространства.
Слайд 18Числовая последовательность
Это частный случай функции.
Функция заданная на множестве натуральных чисел
Слайд 19Термины и символы:
Числа образующие последовательность , называются членами последовательности
у1, у2,
Число стоящее на первом месте, называется первым членом последовательности- у1 )Число стоящее на втором месте, вторым членом последовательности- у2
Число стоящее на n-Ом ,называется n-ым членом последовательности- уn
Слайд 20Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с
- формулой n-го члена( аналитический)
Словесный способ задания
Формулу, задающую числа Фибоначчи, называют рекуррентной (от латинского слова recurro – возвращаться), а соответствующий способ задания последовательности – рекуррентным способом.
Табличный способ задания
Слайд 21Указывается формула n-го члена последовательности.
Пример. Последовательность квадратов натуральных чисел
1, 4,
Пример. Если то
при n=2 ,
при n=20 и т.д.
Слайд 22Правило составления последовательности выражается словесным описанием.
Примеры.
1) Последовательность простых двузначных чисел, меньших
11, 13, 17, 19, 23, 29. 31, 37. 41, 43, 47;
2) Бесконечная последовательность приближений иррационального числа =
=1, 732050808…: 2, 1,7, 1,73, 1,732, 1, 7321, …
Слайд 23Указывается правило позволяющее вычислить n-й член данной последовательности, если известны все
Пример. У1=1, уn=уn-1∙n, если n≥2. Вычислим несколько первых членов этой последовательности: 1, 2, 6, 24, 120, … . Можно убедиться в том, что n-й член данной последовательности равен произведению первых n натуральных чисел: уn=n!
Слайд 24Свойства числовой
последовательности.
Обладает такими же свойствами ,как
Функция: убывающая у1> у2> у3……..
возрастающая у1
Конечная
Бесконечная
Ограниченная
Слайд 25Решение задач
Выпишите первые несколько членов последовательности натуральных чисел, кратных 3, взятых
Перечислите члены последовательности (хn), которые расположены между: а) х31 и х35, б) хn-2 и xn+2.
Найдите первые шесть членов последовательности, заданной формулой n- го члена: хn = 2n – 1.
Выпишите первые пять членов последовательности (аn), если а1 = 1, аn+1 = аn +1.
Слайд 26Самостоятельная работа:
Последовательность (bn) задана формулой bn =
Вычислите b2 , b3 , b4 , b5 члены последовательности (bn ), если известно, что b1=10 и bn+1 = bn + 3.