- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Математические физкультминутки
Содержание
- 1. Презентация по математике Математические физкультминутки
- 2. В программу проведения различных соревнований по математике
- 3. МатематикболВ игре участвуют две команды. Игрокам
- 4. 2. Кто быстрееВ игре может принимать участие
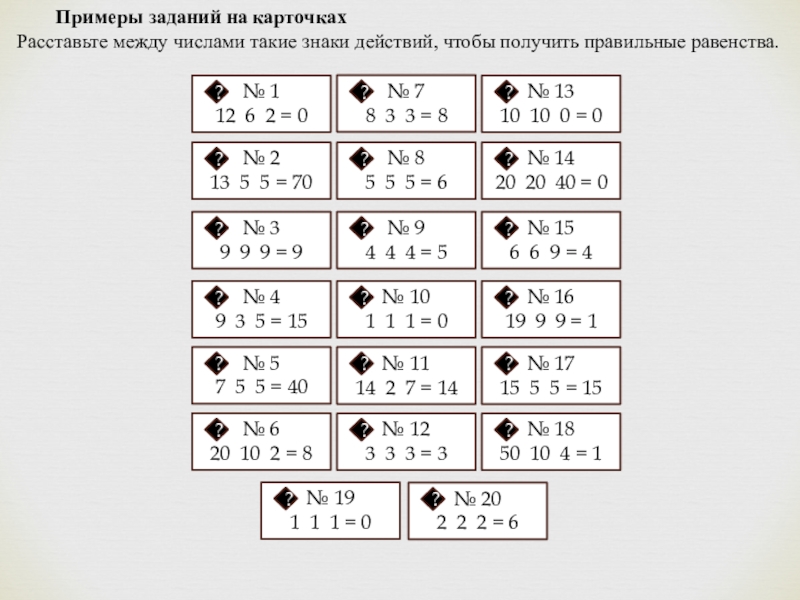
- 5. Примеры заданий на карточкахРасставьте между числами такие знаки действий, чтобы получить правильные равенства.
- 6. Ответы12:6-2=0;13*5-5=70;9-9+9=9;9:3*5=15;7-5+5=40;20-10-2=8;8*3:3=8;5+5:5=6;4:4+4=5;1:1-1=0;14:2+7=14;3+3-3=3;10-10+0=0;20+20-40=0;6*6:9=4;19-9-9=1;15:5*5=15;50:10-4=1;1*1-1=0;2+2*2=6;
- 7. 3. ФизкультминуткаВ игре принимают участие все желающие.
- 8. 5. Вверх по лестницеВ игре может принимать
- 9. 6. Что больше?В игре может принимать участие
- 10. 7. Кто быстрееВ игре может принимать участие
- 11. 8. Округление чиселВ игре может принимать участие
- 12. 9. Попади в цельВ игре может принимать
В программу проведения различных соревнований по математике можно включать игры и конкурсы, в которых решение задач сочетаются с физическими упражнениями – своеобразные физкультминутки. Такие конкурсы помогают снять напряжение, возникающее в ходе соревнований, разрядить обстановку, привлечь внимание,
Слайд 2В программу проведения различных соревнований по математике можно включать игры и
конкурсы, в которых решение задач сочетаются с физическими упражнениями – своеобразные физкультминутки. Такие конкурсы помогают снять напряжение, возникающее в ходе соревнований, разрядить обстановку, привлечь внимание, повысить интерес к игре и, в конечном счете, к математике. Кроме того, такие игры можно проводить и на заседаниях математического кружка, и во время перемен, и даже на прогулках и в походах. Предлогаю примеры игр и конкурсов, в которых физические упражнения сочетаются с решением задач по теме «Натуральные числа».
Слайд 3 Математикбол
В игре участвуют две команды. Игрокам заранее предлагают продумать вопросы
по теме «Натуральные числа». Во время игры команды выстраиваются в линию друг на против друга. Один из игроков первой команды задает вопрос и бросает мяч игроку второй команды. Тот должен поймать мяч, ответить на вопрос, задать свой и бросить мяч игроку первой команды. За пойманный мяч и правильный ответ на вопрос команда получает 2 балла. Если не удалось поймать мяч или ответить на вопрос – 1 балл.
Примеры вопросов по теме «Натуральные числа»
Как называют числа, которые используют для счета предметов?
Назовите наименьшее натуральное число.
Назовите наибольшее натуральное число.
Как называют знаки, которые используют для записи чисел?
Сколько разрядов в классе миллионов?
Назовите наименьший разряд в классе тысяч.
Назовите наименьшее двузначное число.
Какое число в ряду натуральных чисел следует за числом 140 070?
Примеры вопросов по теме «Натуральные числа»
Как называют числа, которые используют для счета предметов?
Назовите наименьшее натуральное число.
Назовите наибольшее натуральное число.
Как называют знаки, которые используют для записи чисел?
Сколько разрядов в классе миллионов?
Назовите наименьший разряд в классе тысяч.
Назовите наименьшее двузначное число.
Какое число в ряду натуральных чисел следует за числом 140 070?
Слайд 42. Кто быстрее
В игре может принимать участие любое количество команд. Все
команды располагаются в определенном месте. На некотором расстоянии (пример 10 м) от этого места на столе раскладываются карточки, на которых написаны задания. По сигналу по одному игроку от каждой команды подбегают к столу, берут по одной карточке и приносят их командам. Пока члены команды выполняют задание, следующий игрок бежит за карточкой и т.д. Побеждает команда, которая правильно выполнила больше заданий.
Слайд 5Примеры заданий на карточках
Расставьте между числами такие знаки действий, чтобы получить
правильные равенства.
Слайд 6Ответы
12:6-2=0;
13*5-5=70;
9-9+9=9;
9:3*5=15;
7-5+5=40;
20-10-2=8;
8*3:3=8;
5+5:5=6;
4:4+4=5;
1:1-1=0;
14:2+7=14;
3+3-3=3;
10-10+0=0;
20+20-40=0;
6*6:9=4;
19-9-9=1;
15:5*5=15;
50:10-4=1;
1*1-1=0;
2+2*2=6;
Слайд 73. Физкультминутка
В игре принимают участие все желающие. Нужно рассказать таблицу умножения
на заданное число, выполняя приседания. Побеждает тот, кто быстрее расскажет таблицу умножения, выполнив при этом как можно больше приседаний.
4. Эстафета
В игре принимают участие две команды. Игроки каждой команды выстраиваются в колонну и по очереди подбегают к столам, на которых лежат листы с написанными на них заданиями на нахождение значения выражения. Первый игрок, выполнив первое действие, возвращает и передает эстафетную палочку (ручку) второму игроку и т.д. Побеждает команда, которая первой выполнит задание, допустив меньше ошибок.
Примеры заданий на нахождение значений выражений
126:9*11+1250:10*8+6*141-25*80.
Ответ. 0.
2. 504:9*10+416:4*5+8*115-15*24.
Ответ. 0.
4. Эстафета
В игре принимают участие две команды. Игроки каждой команды выстраиваются в колонну и по очереди подбегают к столам, на которых лежат листы с написанными на них заданиями на нахождение значения выражения. Первый игрок, выполнив первое действие, возвращает и передает эстафетную палочку (ручку) второму игроку и т.д. Побеждает команда, которая первой выполнит задание, допустив меньше ошибок.
Примеры заданий на нахождение значений выражений
126:9*11+1250:10*8+6*141-25*80.
Ответ. 0.
2. 504:9*10+416:4*5+8*115-15*24.
Ответ. 0.
Слайд 85. Вверх по лестнице
В игре может принимать участие две команды, игроки
которых находятся «за чертой» – линией, проведенной на некотором расстоянии от доски. На доске (или на плакате) изображают лестницу, на каждой ступеньке которой нужно написать такое число, чтобы, выполнив действие, получить число, стоящее ступенькой выше. Игроки по очереди подбегают к доске и записывают нужные числа. Причем следующий игрок может вступить в игру только после того, как предыдущий вернулся за обозначенную линию. Побеждает команда, которая первой достигает верхней ступеньки.
Слайд 96. Что больше?
В игре может принимать участие две команды. Игрокам на
спины прикрепляют листы бумаги, на которых написаны цифры от 0 до 9 и знаки « > » и « < ». Каждой команде предлагают сравнить числа. По команде игроки должны построиться в одну линию спиной к зрителям так, чтобы можно было прочитать полученное неравенство. Побеждает команда, которая быстрее составит правильное неравенство.
Примеры чисел для сравнения
(Каждая цифра использована не более одного раза.)
2 890 и 3 154;
1 052 и 987;
9 786 и 10 324;
17 450 и 8 563.
Примеры чисел для сравнения
(Каждая цифра использована не более одного раза.)
2 890 и 3 154;
1 052 и 987;
9 786 и 10 324;
17 450 и 8 563.
Слайд 107. Кто быстрее
В игре может принимать участие две команды. Игрокам на
спины прикрепляют листы бумаги, на которых написаны цифры от 0 до 9 и знаки математических действий. Каждой команде предлагают выполнить задание на нахождение значения выражения. По команде игроки должны построиться в одну линию спиной к зрителям пример и ответ. Побеждает команда, которая быстрее составит правильное выражение.
Примеры заданий на нахождение значений выражений
(Каждая цифра использована не более одного раза)
204:3+97;
Ответ. 165.
2. 328:4-67;
Ответ. 15.
3. 25*9+84+7;
Ответ. 316.
36*5+4+97.
Ответ. 281.
Примеры заданий на нахождение значений выражений
(Каждая цифра использована не более одного раза)
204:3+97;
Ответ. 165.
2. 328:4-67;
Ответ. 15.
3. 25*9+84+7;
Ответ. 316.
36*5+4+97.
Ответ. 281.
Слайд 118. Округление чисел
В игре может принимать участие две команды. На столе
раскладывают карточки, на которых написаны цифры. Каждой команде задают число (желательно, чтобы количество цифр в числе совпадало с количеством игроков в команде). По сигналу игроки по очереди подбегают к столу и берут по одной карточке, чтобы составить заданное число. Когда числа составлены, ведущий объявляет, до какого разряда их нужно округлить. После этого игроки снова по одному подбегают к столу, берут нужные карточки и составляют округленные числа. Побеждает команда, которая первой правильно составит заданные числа.
Примеры чисел для округления
(В каждой паре примеров одинаковые количество цифр, которые нужно заменить.)
Число 359 740 округлите до сотен.
Ответ. 359 740 ≈ 359 700.
Число 152 867 округлите до десятков.
Ответ. 152 867 ≈ 152 870.
Число 235 680 округлите до десятков тысяч.
Ответ. 235 680 ≈ 240 000.
Число 712 349 округлите до сотен тысяч.
Ответ. 712 349 ≈ 700 000.
Примеры чисел для округления
(В каждой паре примеров одинаковые количество цифр, которые нужно заменить.)
Число 359 740 округлите до сотен.
Ответ. 359 740 ≈ 359 700.
Число 152 867 округлите до десятков.
Ответ. 152 867 ≈ 152 870.
Число 235 680 округлите до десятков тысяч.
Ответ. 235 680 ≈ 240 000.
Число 712 349 округлите до сотен тысяч.
Ответ. 712 349 ≈ 700 000.
Слайд 129. Попади в цель
В игре может принимать участие любое количество команд.
На кегли наклеивают цифры и выстраивают их в одну линию. Каждая из команд получает задание: например, решить уравнение. После этого игроки команд сбивают мячом кегли с цифрами, из которых можно составить число, являющееся корнем уравнения. (При необходимости можно использовать несколько попыток.) Право первой бросать мяч получает та команда, которая первой решила уравнение. Побеждает команда, игроки которой правильно решили уравнение и сбили нужные кегли, используя наименьшее число попыток.
Примеры уравнений
(Корни уравнений – трехзначные числа, состоящие из разных цифр.)
1097 – 4х = 569.
Ответ. 132.
986 – (х+25) = 156.
Ответ. 825.
х:2-101=250.
Ответ. 702.
756+(630-х)=249.
Ответ. 120.
Примеры уравнений
(Корни уравнений – трехзначные числа, состоящие из разных цифр.)
1097 – 4х = 569.
Ответ. 132.
986 – (х+25) = 156.
Ответ. 825.
х:2-101=250.
Ответ. 702.
756+(630-х)=249.
Ответ. 120.