- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Ключевые задачи на касательную
Содержание
- 1. Презентация по математике Ключевые задачи на касательную
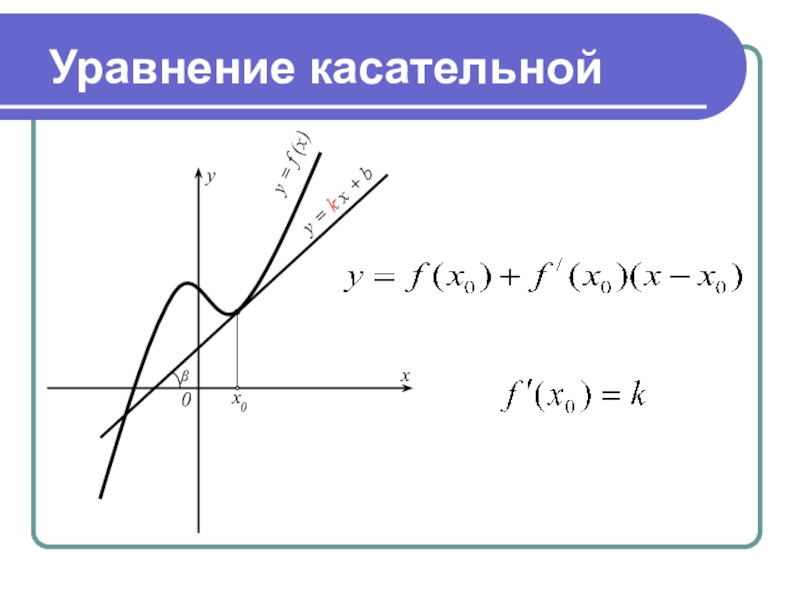
- 2. Уравнение касательной
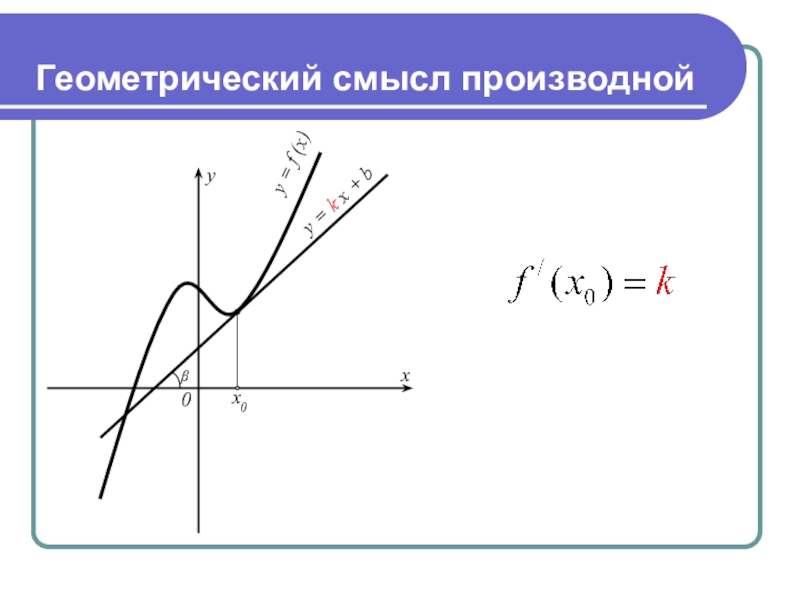
- 3. Геометрический смысл производной
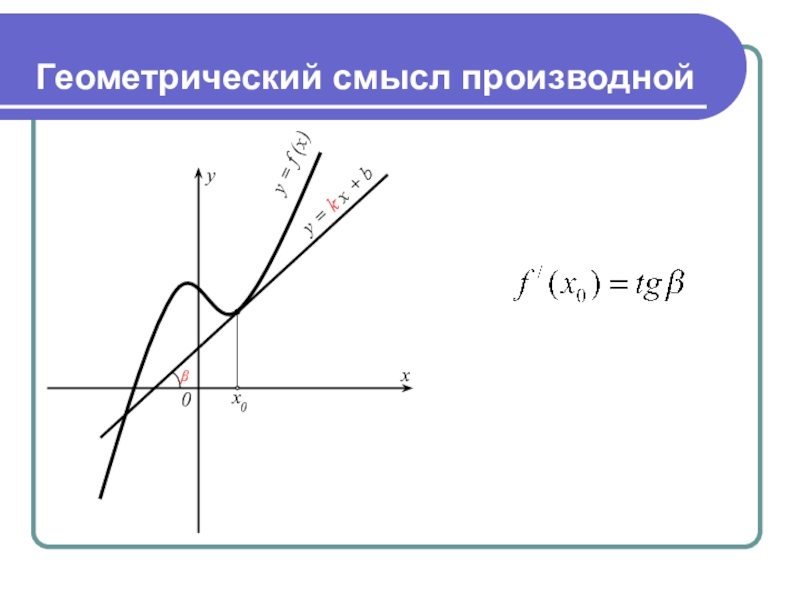
- 4. Геометрический смысл производной
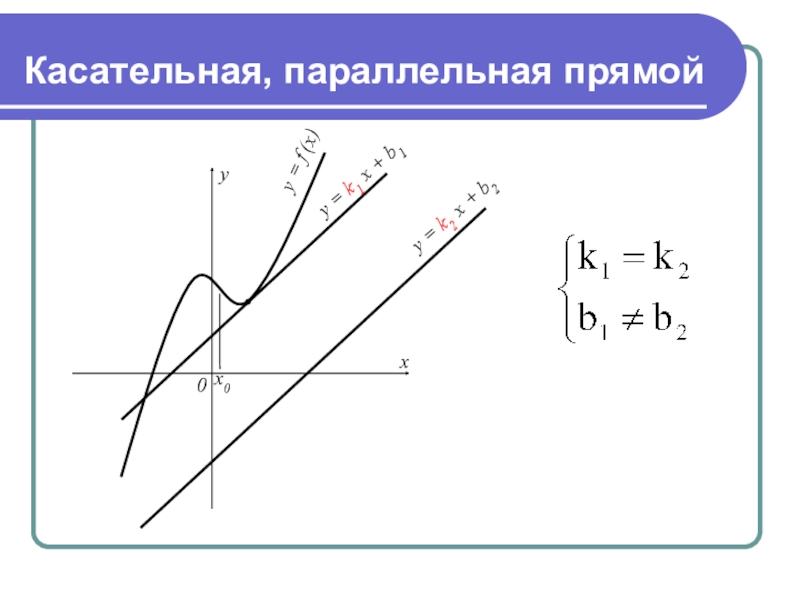
- 5. Касательная, параллельная прямойy = k2 x + b2y = k1 x + b1
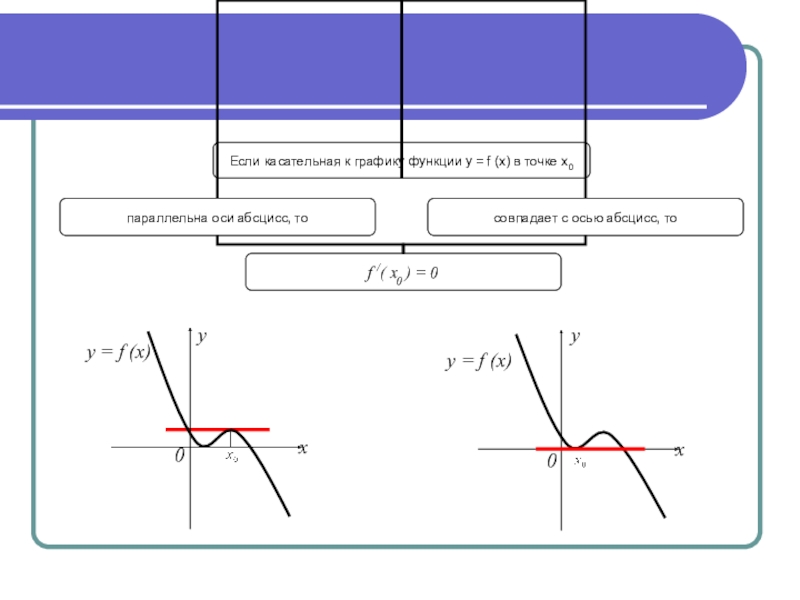
- 6. 00yxy = f (x)xy = f (x)y
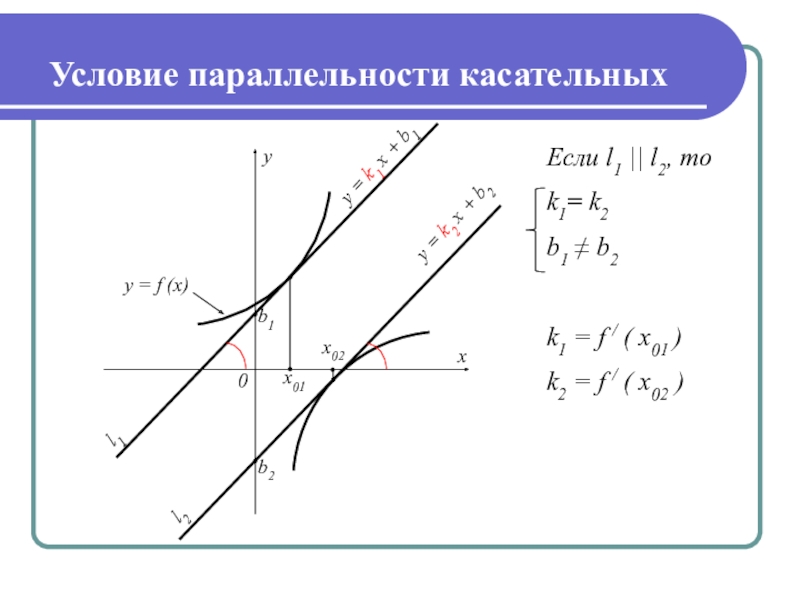
- 7. Условие параллельности касательныхy = k1 x + b1l2
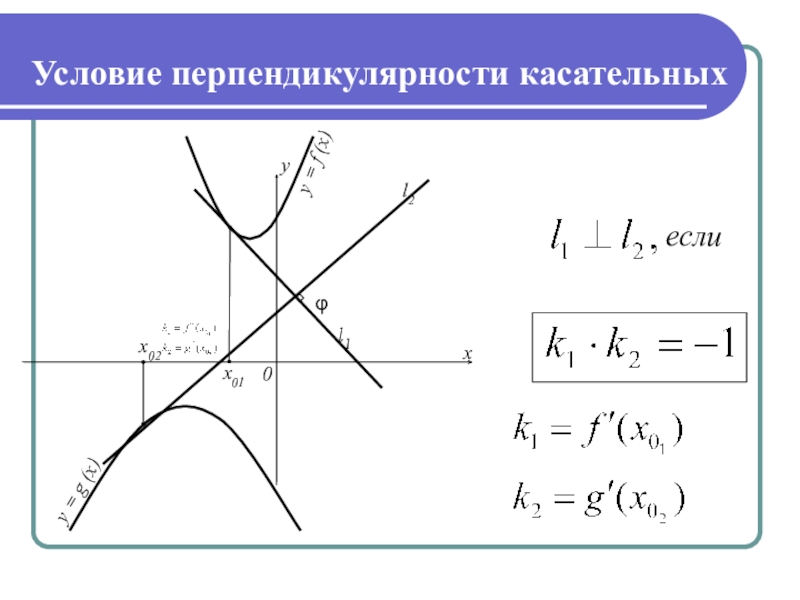
- 8. Условие перпендикулярности касательныхy = f (x)y = g (x)yx0φx02x01l1l2если
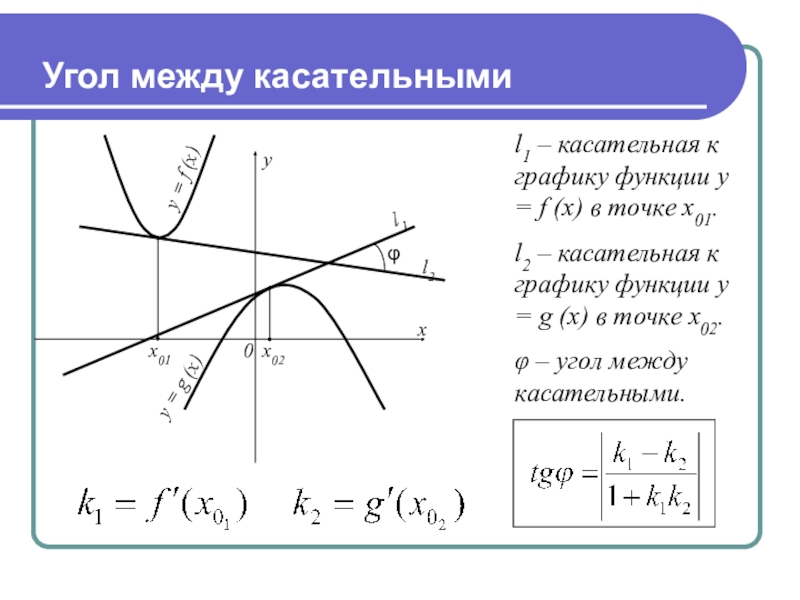
- 9. Угол между касательнымиy = f (x)l1 –
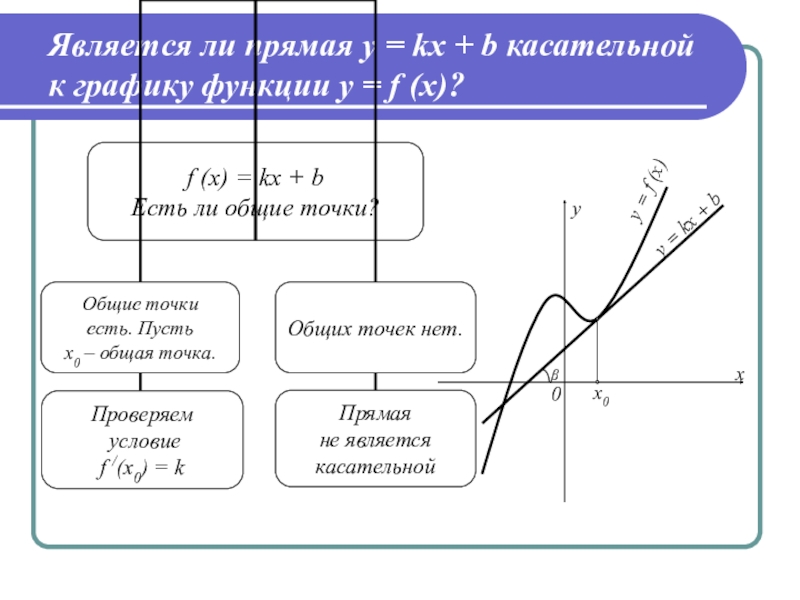
- 10. Является ли прямая y = kx + b касательной к графику функции y = f (x)?
- 11. Вывод Прямая y = kx + b является
- 12. y = f (x)y = g (x)y
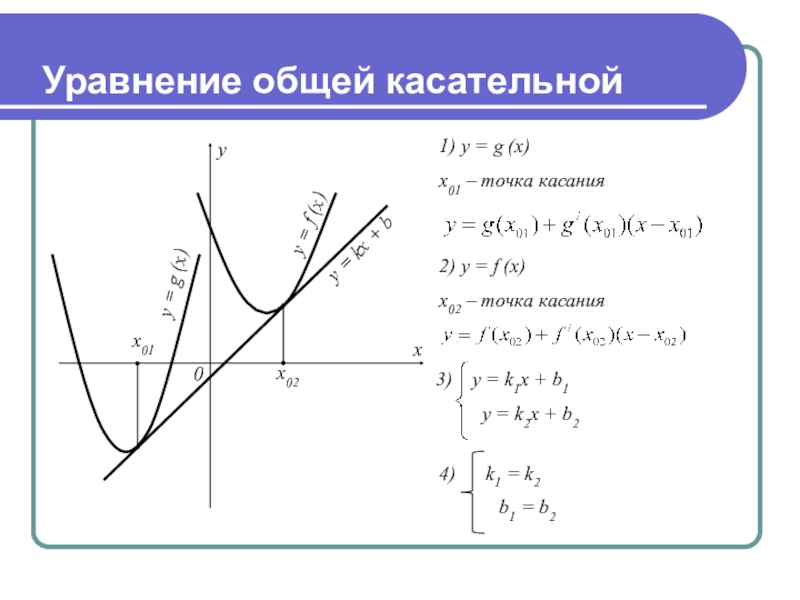
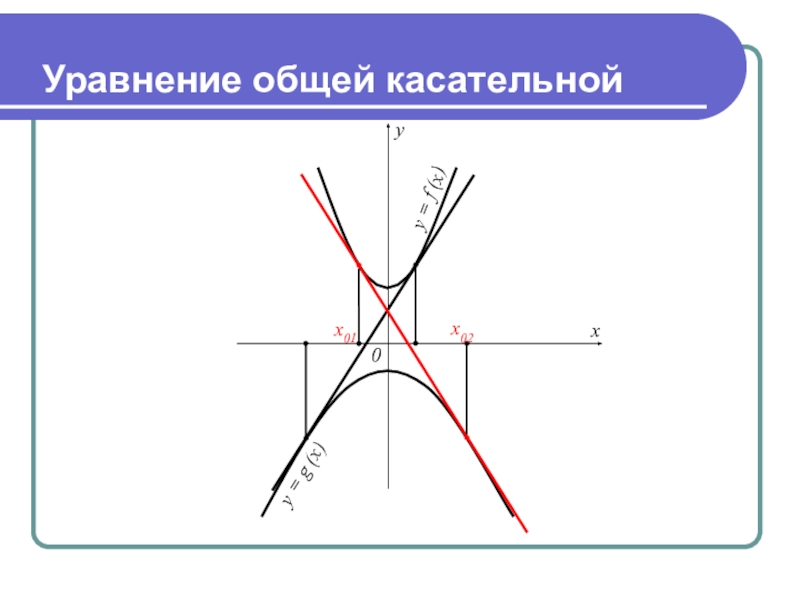
- 13. Уравнение общей касательной
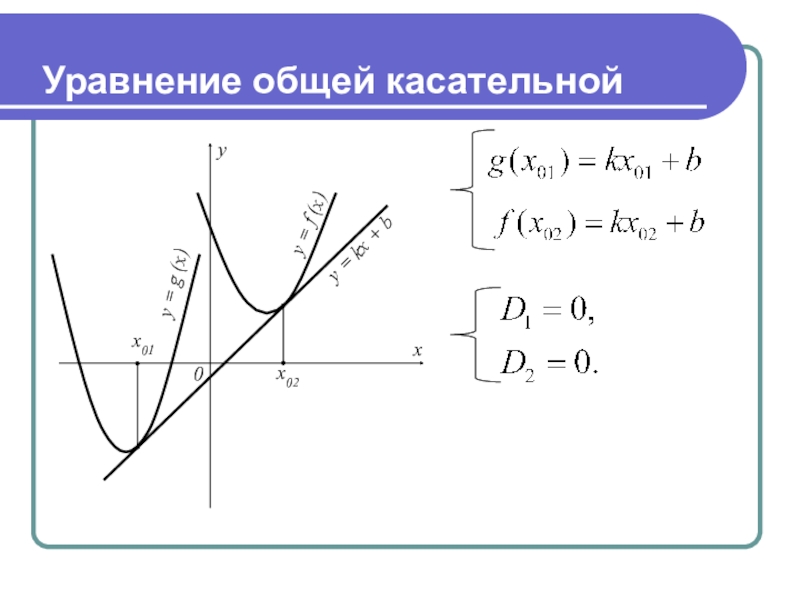
- 14. Уравнение общей касательной
- 15. Уравнение касательной, проходящей через заданную точкуУравнение касательной в общем видеТ.к. M (a;b) принадлежит касательной, то
- 16. На рисунке изображен график функции
- 17. На рисунке изображен график функциии касательная к
- 18. На рисунке изображен график функциии касательная к
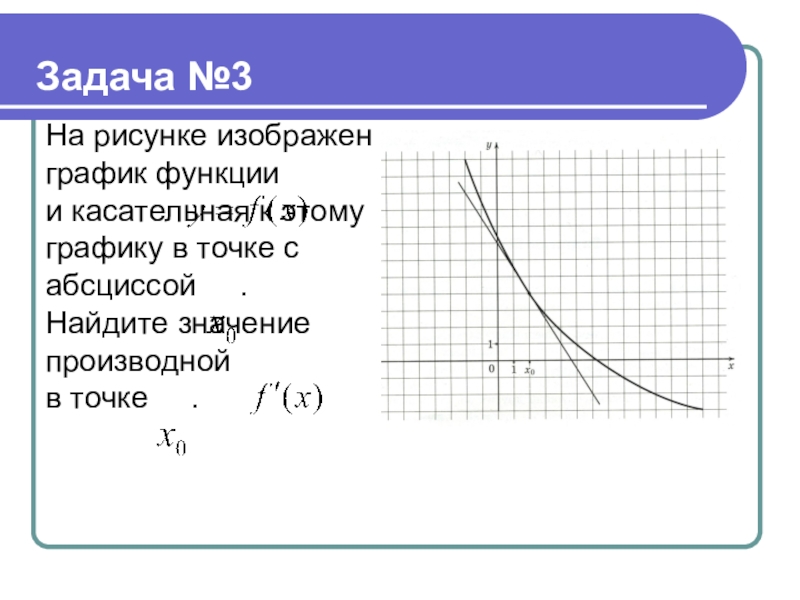
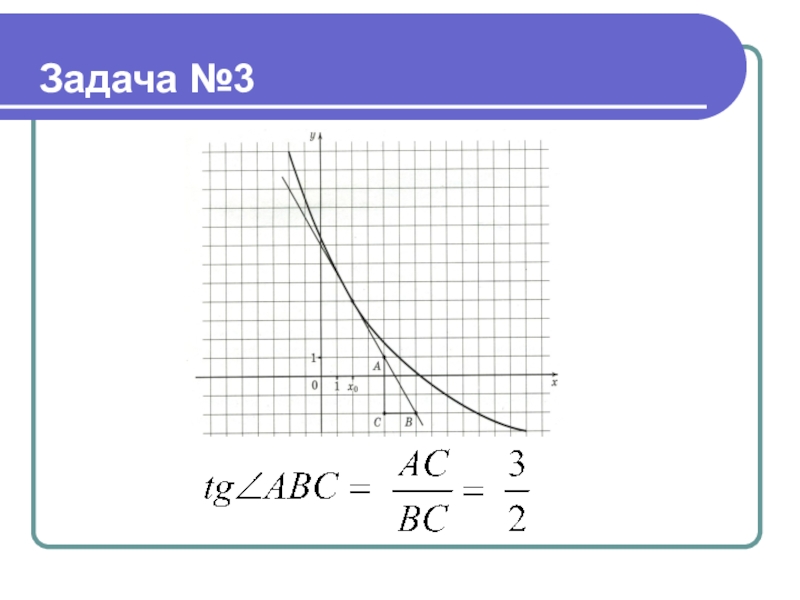
- 19. Задача №3
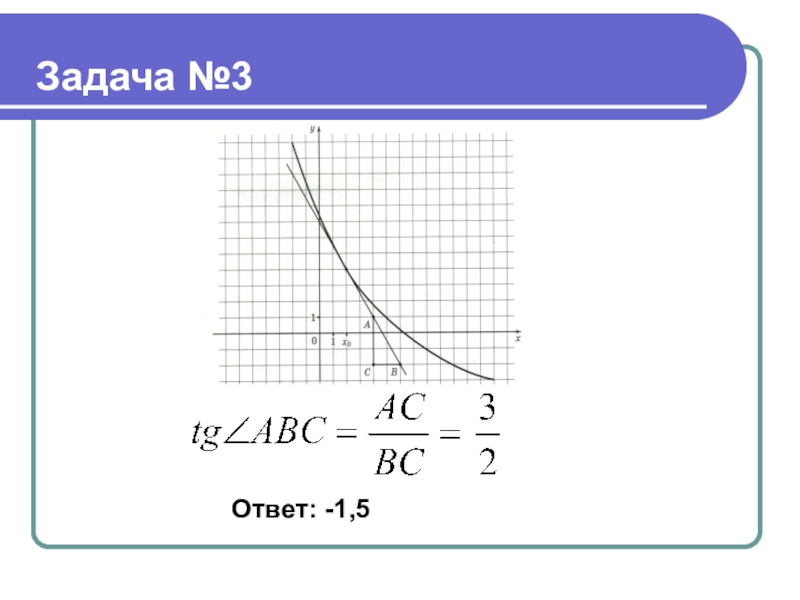
- 20. Задача №3Ответ: -1,5
Уравнение касательной
Слайд 9Угол между касательными
y = f (x)
l1 – касательная к графику функции
y = f (x) в точке x01.
l2 – касательная к графику функции y = g (x) в точке x02.
φ – угол между касательными.
l2 – касательная к графику функции y = g (x) в точке x02.
φ – угол между касательными.
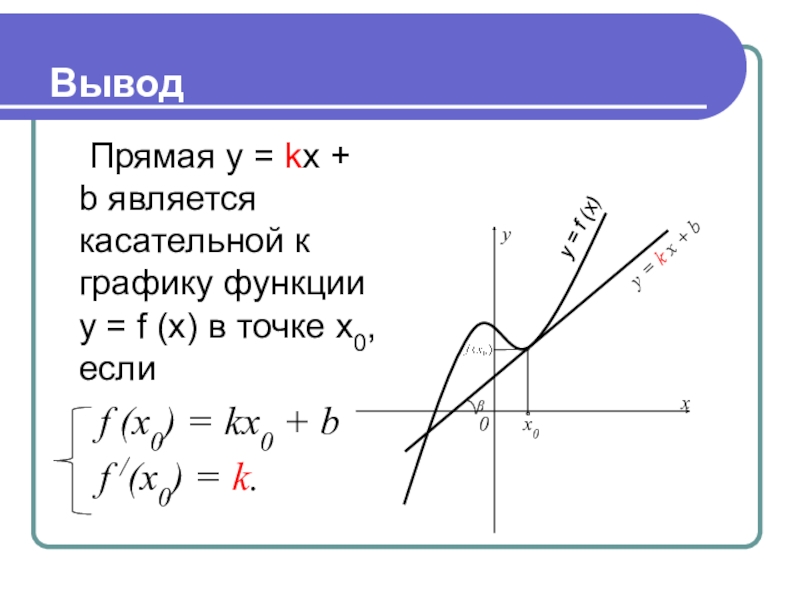
Слайд 11Вывод
Прямая y = kx + b является касательной к графику функции
y = f (x) в точке x0, если
f (x0) = kx0 + b
f /(x0) = k.
f (x0) = kx0 + b
f /(x0) = k.
y = k x + b
y = f (x)
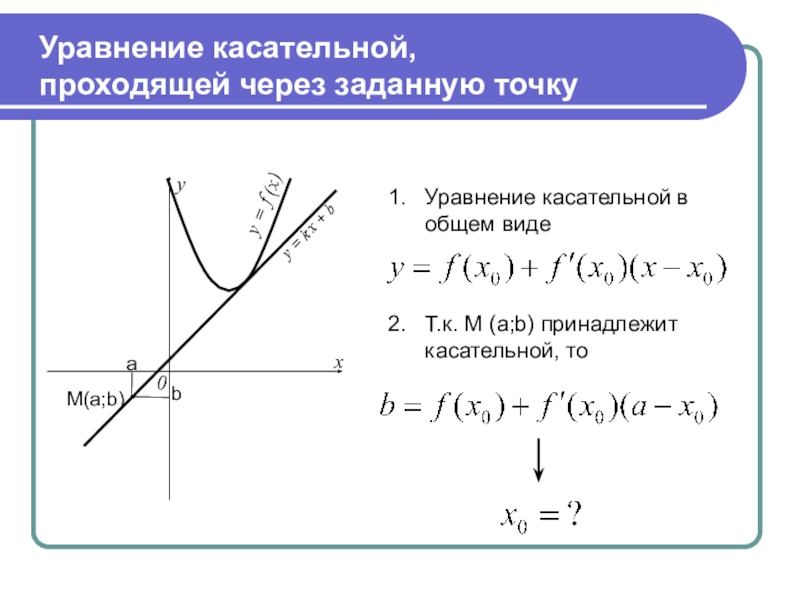
Слайд 15Уравнение касательной,
проходящей через заданную точку
Уравнение касательной в общем виде
Т.к. M (a;b)
принадлежит касательной, то
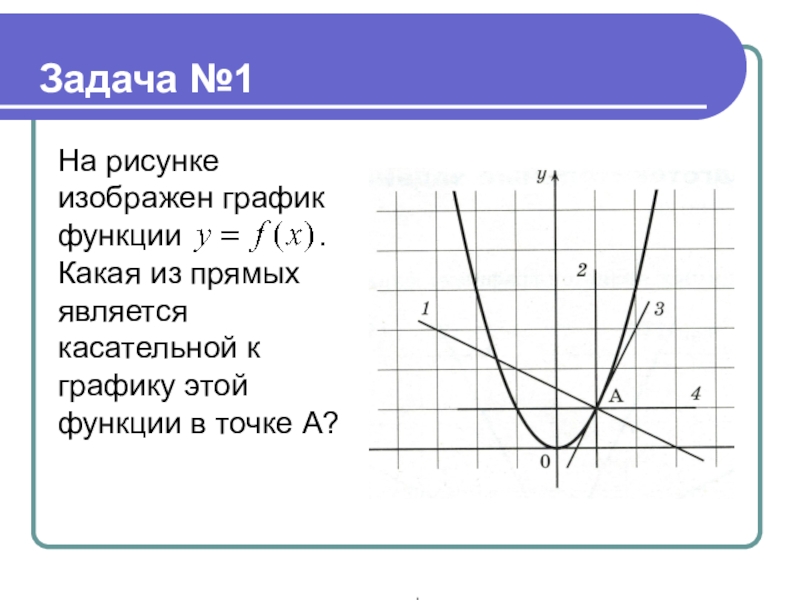
Слайд 16На рисунке изображен график функции
.
Какая из прямых является касательной к графику этой функции в точке А?
Какая из прямых является касательной к графику этой функции в точке А?
Задача №1
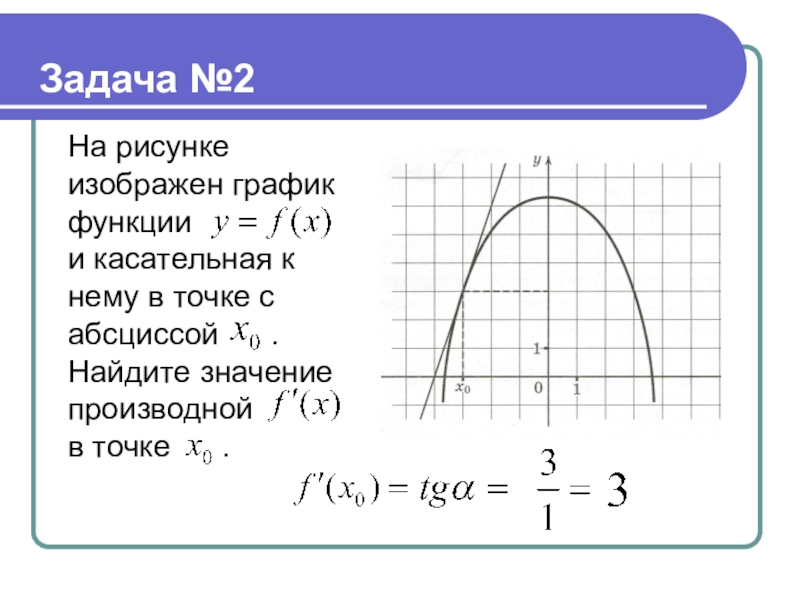
Слайд 17На рисунке изображен график функции
и касательная к нему в точке с
абсциссой .
Найдите значение производной
в точке .
Найдите значение производной
в точке .
Задача №2
Слайд 18На рисунке изображен график функции
и касательная к этому графику в точке
с абсциссой .
Найдите значение производной
в точке .
Найдите значение производной
в точке .
Задача №3