- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике История тригонометрии
Содержание
- 1. Презентация по математике История тригонометрии
- 2. Тригонометрия Слово «тригонометрия» впервые встречается
- 3. СИНУС Длительную историю имеет понятие
- 4. В IV-V веках появился
- 5. КОСИНУС Слово косинус намного моложе. Косинус
- 6. ТАНГЕНС и КОТАНГЕНС Тангенсы возникли
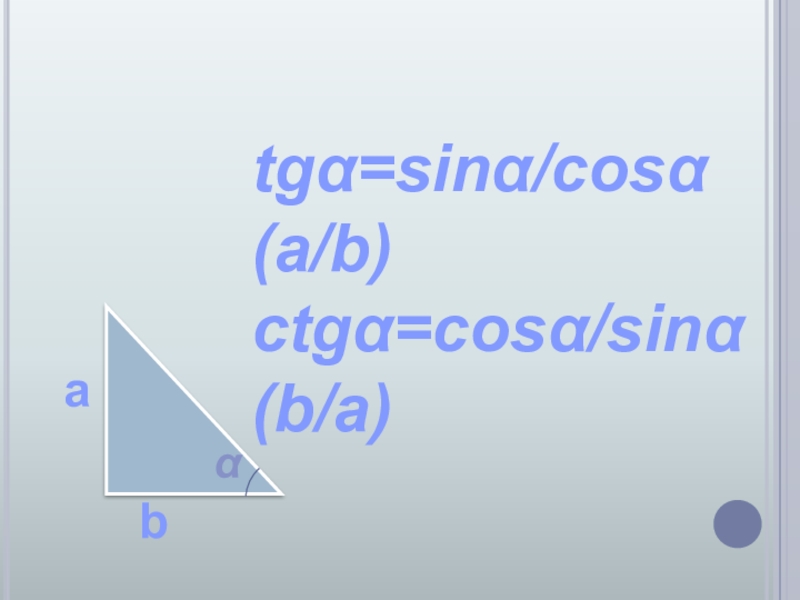
- 7. tgα=sinα/cosα (a/b)ctgα=cosα/sinα (b/a)baα
- 8. Длительное время тригонометрия развивалась
- 9. Принципиальное значение имело составление
- 10. Современный вид тригонометрии придал
Тригонометрия Слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое, переводится как «наука об измерении треугольников»
Слайд 2Тригонометрия
Слово «тригонометрия» впервые встречается в 1505 году в
заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое, переводится как «наука об измерении треугольников»
Слайд 3СИНУС
Длительную историю имеет понятие синуса. Фактически различные отношения
отрезков треугольника и окружности(а по существу и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции- Евклида, Архимеда, Апполония Пергского.
Архимед
Евклид
Апполоний
Пергский
Слайд 4 В IV-V веках появился уже специальный термин в
трудах по астрономии великого индийского учёного Ариабхаты (476-ок.550). Отрезок CB он назвал ардхаджива (ардха –половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в
XIIвеке оно было заменено латинским синус (sinus –изгиб, кривизна).
XIIвеке оно было заменено латинским синус (sinus –изгиб, кривизна).
СИНУС
Слайд 5КОСИНУС
Слово косинус намного моложе. Косинус – это сокращенное латинское
выражение complementy sinus, то есть «дополнительный синус» ( или иначе «синус дополнительной дуги»)
Слайд 6ТАНГЕНС и КОТАНГЕНС
Тангенсы возникли в связи с решением
задачи об определении длины тени. Тангенс, а также котангенс, введен в XI в. Арабским математиком Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты в XIVвеке сначала английским ученым Т.Брадвердином, а позднее немецким математиком Региомонтаном(1467г.). Само название «тангенс», происходящее от латинского слова «tanger» (касаться), появилось лишь в 1583 году.
Слайд 8 Длительное время тригонометрия развивалась как часть геометрии. Пожалуй,
наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затмений и т.д.)
?
Слайд 9 Принципиальное значение имело составление К.Птолемеем первой таблицы синусов
(долгое время она называлась таблицей хорд). Появилось практическое средство решения прикладных задач.
Птолемей
Слайд 10 Современный вид тригонометрии придал крупнейший математик XVIII столетия
Леонард Эйлер (1707-1783),швейцарец по происхождению, долгие годы работавший в России и являвшийся членом Петербургской академии наук. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. Всё это малая доля того, что за долгую жизнь Эйлер успел сделать в тригонометрии: он оставил свыше 800 работ, доказал многие, ставшие впоследствии классическими теоремы.
Л.Эйлер