- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Интервальные оценки параметров распределения
Содержание
- 1. Презентация по математике Интервальные оценки параметров распределения
- 2. План:Точность оценки. Доверительная вероятность (надежность). Доверительный интервал.Интервальные
- 3. I. Точность оценки. Доверительная вероятность (надежность).
- 4. I. Точность оценки. Доверительная вероятность (надежность). Доверительный интервал. Доверительный интервал
- 5. Ежи Нейман(1894-1981)Рональд Фишер(1890-1962)
- 6. II. Интервальные оценки параметров нормального распределения. X~N(a,σ)
- 7. 1) Доверительный интервал для оценки математического ожидания
- 8. 1) Доверительный интервал для оценки математического ожидания
- 9. ПРИМЕР 1. Случайная величина прочности бетона X
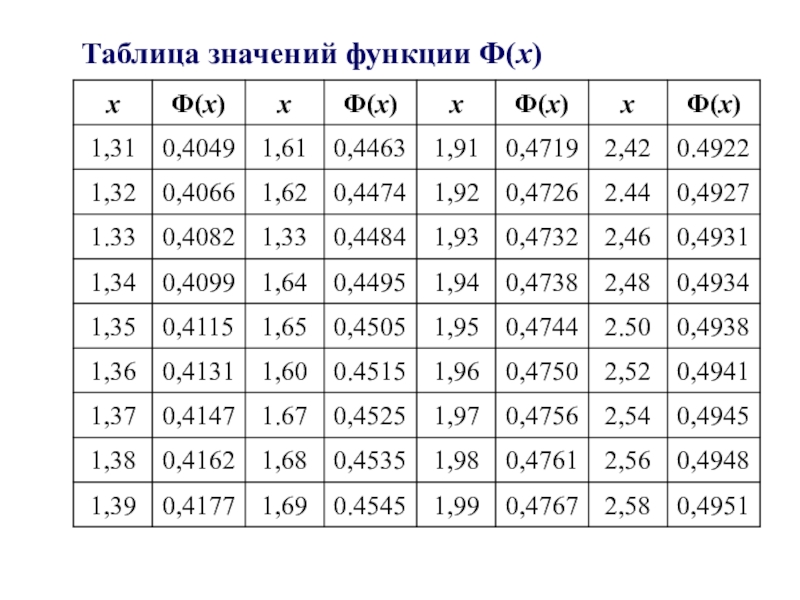
- 10. Таблица значений функции Ф(х)
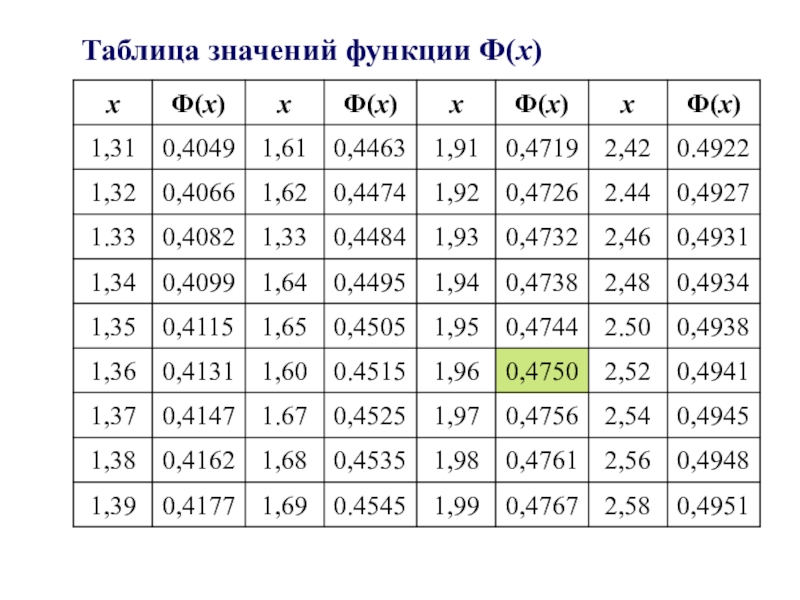
- 11. Таблица значений функции Ф(х)
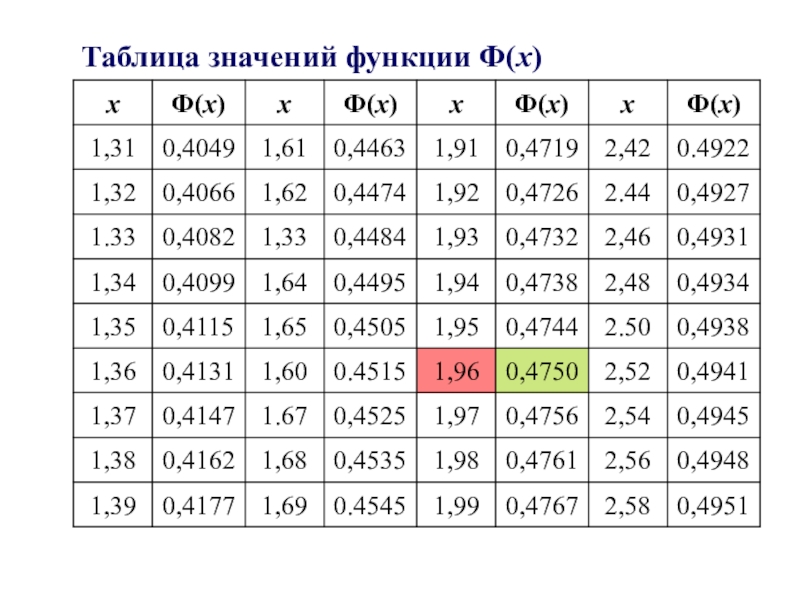
- 12. Таблица значений функции Ф(х)
- 13. ПРИМЕР 2.Найти минимальный объем выборки, на основании
- 14. 2) Доверительный интервал для оценки математического ожидания
- 15. ПРИМЕР 3.Из генеральной совокупности извлечена выборка Оценить
- 16. Таблица значений
- 17. Таблица значений
- 18. Таблица значений
- 19. Таблица значений
- 20. Таблица значений
- 21. 3) Доверительный интервал для оценки среднего квадратического
- 22. ПРИМЕР 4.Количественный признак X генеральной совокупности распределен
- 23. III. Оценка истинного значения измеряемой величины и
- 24. ПРИМЕР 5.Найти 95% доверительный интервал для истинного
- 25. ПРИМЕР 6.Произведено 12 измерений расстояния новым дальномером.
- 26. Литература:Гмурман В.Е. Теория вероятностей и математическая статистика.2.
- 27. Домашнее задание Глава шестнадцатая, §14-§19. [1] Глава десятая, §4. №511, 515. [2]
План:Точность оценки. Доверительная вероятность (надежность). Доверительный интервал.Интервальные оценки параметров нормального распределения.Доверительный интервал для оценки математического ожидания при известном σ. Доверительный интервал для оценки математического ожидания при неизвестном σ.Доверительный интервал для оценки среднего квадратического отклонения σ.Оценка истинного
Слайд 2План:
Точность оценки. Доверительная вероятность (надежность). Доверительный интервал.
Интервальные оценки параметров нормального распределения.
Доверительный
интервал для оценки математического ожидания при известном σ.
Доверительный интервал для оценки математического ожидания при неизвестном σ.
Доверительный интервал для оценки среднего квадратического отклонения σ.
Оценка истинного значения измеряемой величины и точности измерений.
Доверительный интервал для оценки математического ожидания при неизвестном σ.
Доверительный интервал для оценки среднего квадратического отклонения σ.
Оценка истинного значения измеряемой величины и точности измерений.
Слайд 3I. Точность оценки.
Доверительная вероятность (надежность).
Доверительный интервал.
γ – доверительная вероятность
(надежность оценки)
δ > 0 – точность оценки
δ > 0 – точность оценки
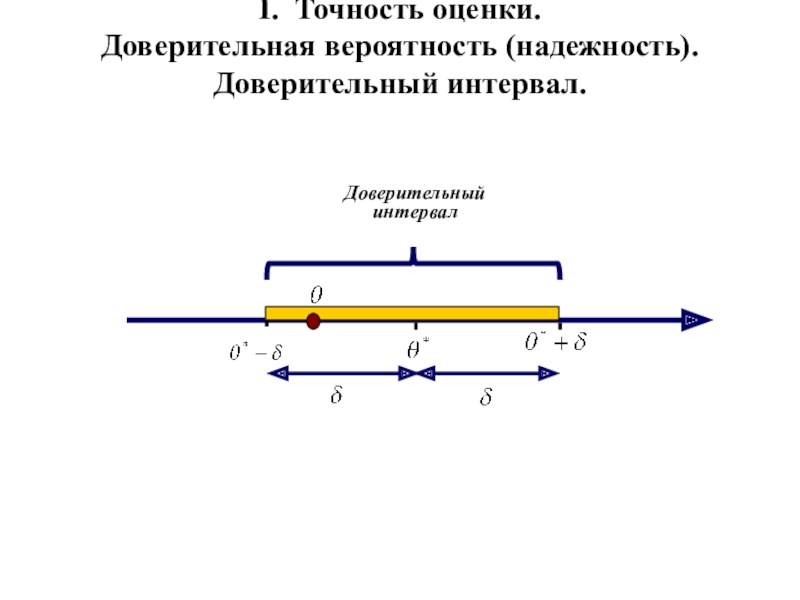
Слайд 4I. Точность оценки.
Доверительная вероятность (надежность).
Доверительный интервал.
Доверительный
интервал
Слайд 71) Доверительный интервал для оценки математического ожидания при известном σ
Дано: случайная
выборка объема n из генеральной совокупности имеющей нормальное распределение. Среднее квадратическое отклонение σ предполагается известным.
Требуется: оценить математическое ожидание а по его выборочной средней с заданной надежностью γ.
Требуется: оценить математическое ожидание а по его выборочной средней с заданной надежностью γ.
Слайд 81) Доверительный интервал для оценки математического ожидания при известном σ
- точность оценки;
- значение аргумента функции Лапласа, при котором ;
Слайд 9ПРИМЕР 1.
Случайная величина прочности бетона X имеет нормальное распределение с
известным стандартом σ = 3 МПа. Найти доверительный интервал для оценки средней прочности a по выборочной средней =16,8 МПа, если объем выборки n = 36 и задана доверительная вероятность оценки γ = 0,95.
Слайд 13ПРИМЕР 2.
Найти минимальный объем выборки, на основании которой можно было бы
оценить параметры некоторой технической операции с ошибкой, не превышающей 10 и надежностью 0,95, если предположить, что параметр этой технической операции имеет нормальное распределение X~N(a,50)
Слайд 142) Доверительный интервал для оценки математического ожидания при неизвестном σ
X~N(a,σ),
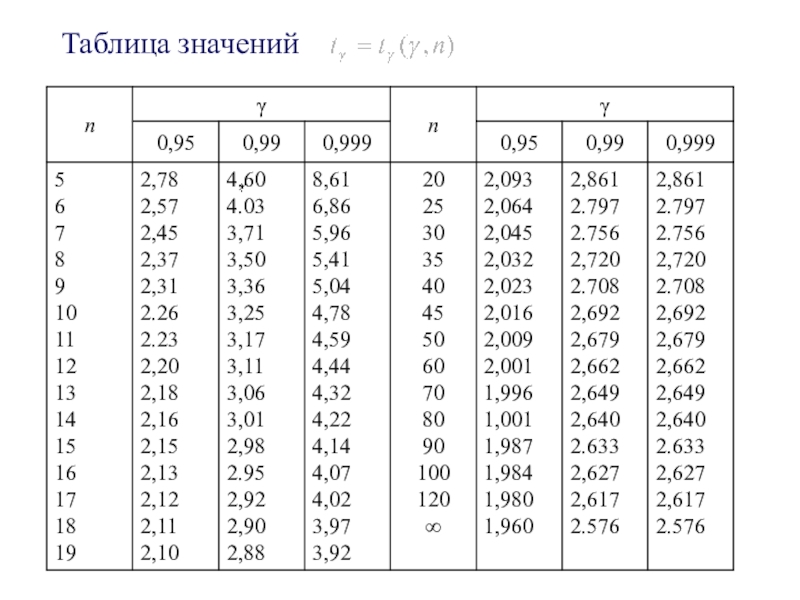
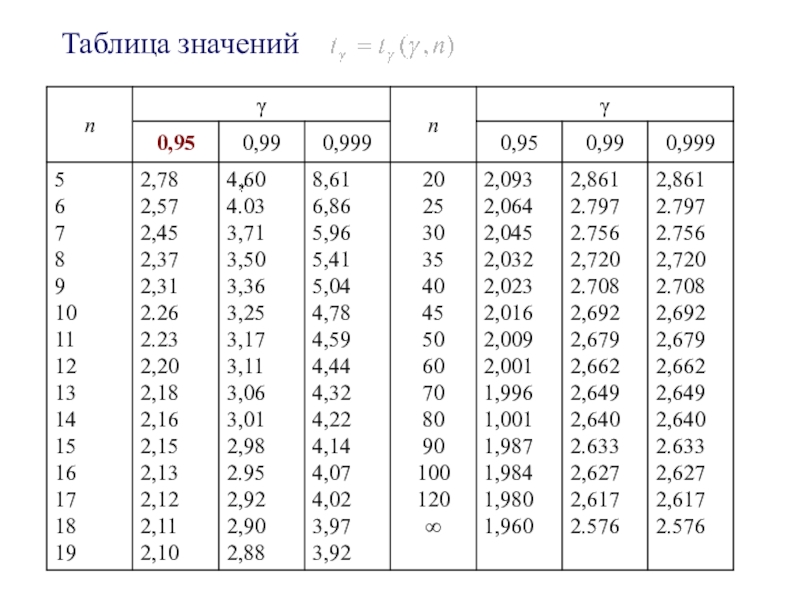
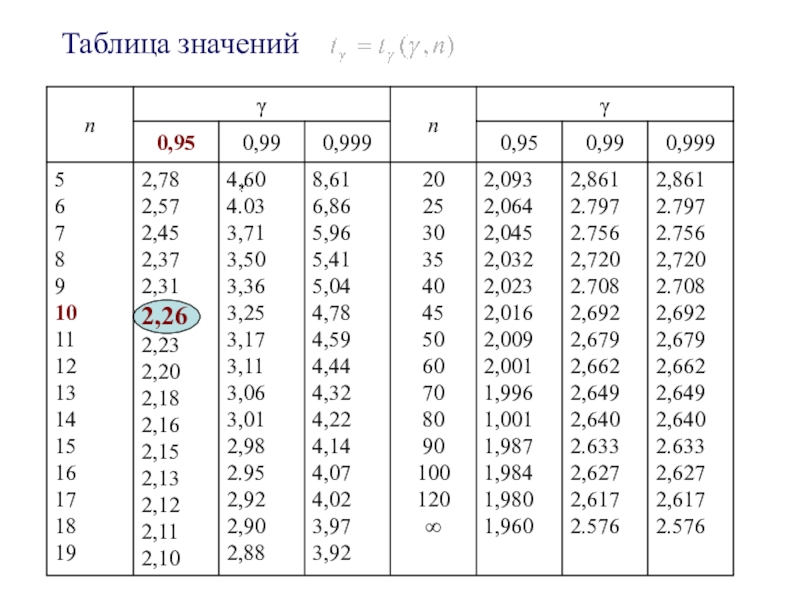
-определяется
по «Таблице значений »
Дано:
Требуется:
-исправленное выборочное среднее
квадратическое отклонение;
γ
n,
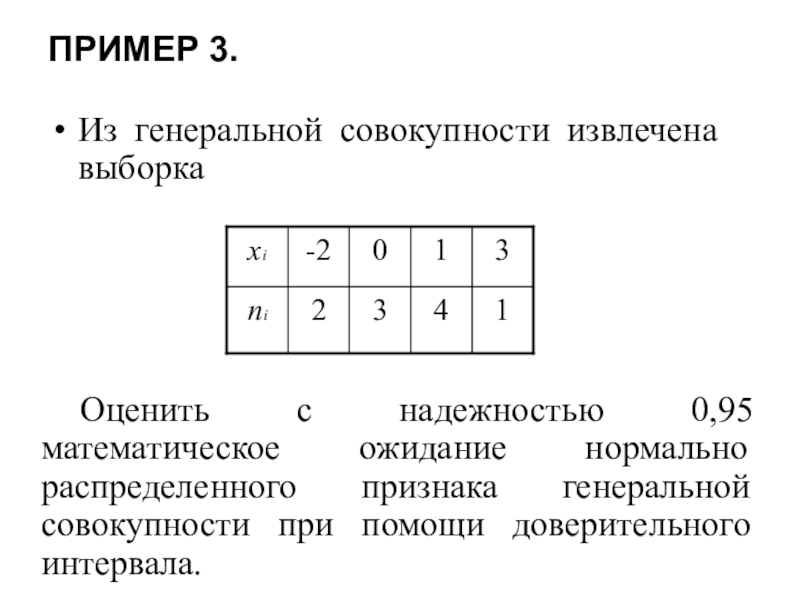
Слайд 15ПРИМЕР 3.
Из генеральной совокупности извлечена выборка
Оценить с надежностью 0,95
математическое ожидание нормально распределенного признака генеральной совокупности при помощи доверительного интервала.
Слайд 213) Доверительный интервал для оценки среднего квадратического отклонения σ нормально распределенного
количественного признака X с заданной надежностью γ
(при q<1)
(при q>1)
-определяется по «Таблице значений q»
s - исправленное выборочное среднее
квадратическое отклонение;
Слайд 22ПРИМЕР 4.
Количественный признак X генеральной совокупности распределен нормально. По выборке объема
п = 25 найдено исправленное выборочное среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.
Слайд 23III. Оценка истинного значения измеряемой величины и точности измерений
Истинное значение
измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.
Точность измерений (точность прибора) характеризуется с помощью среднего квадратического отклонения σ случайных ошибок измерения.
Точность измерений (точность прибора) характеризуется с помощью среднего квадратического отклонения σ случайных ошибок измерения.
Слайд 24ПРИМЕР 5.
Найти 95% доверительный интервал для истинного значения твердости сплава (в
условных единицах), если по результатам измерений получены следующие значения: 14,2; 14,8; 14,0; 14,7; 13,9; 14,8; 15,1; 14,5.
Слайд 25ПРИМЕР 6.
Произведено 12 измерений расстояния новым дальномером. Исправленное среднее квадратическое отклонение
s случайных ошибок измерения оказалось равным 0,6 м. Найти точность прибора с надежностью 0,99.
Слайд 26Литература:
Гмурман В.Е. Теория вероятностей и математическая статистика.
2. Гмурман В.Е. Руководство к
решению задач по теории вероятностей и математической статистике.


















![Презентация по математике Интервальные оценки параметров распределения Домашнее задание Глава шестнадцатая, §14-§19. [1] Глава десятая, §4. №511, 515. [2] Домашнее задание Глава шестнадцатая, §14-§19. [1] Глава десятая, §4. №511, 515. [2]](/img/thumbs/eb103f53a63f10bb62803bc0d26b85d1-800x.jpg)





