- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для учеников 2-4 класс
Содержание
- 1. Презентация по математике для учеников 2-4 класс
- 2. Слайд 2
- 3. Ответьте на вопросыЗнаете ли вы когда, где
- 4. Немного истории…Вначале при счете предметов возникли …
- 5. Натуральные числаНикто не знает, когда впервые появились
- 6. Отрицательные числаОдним из важнейших этапов в развитии
- 7. Отрицательные числаОтрицательные числа появились позднее, чем дроби.
- 8. Ещё немного из истории отрицательных чисел… Несмотря
- 9. Ещё истории…Введение отрицательных чисел и нуля позволило расширить множество натуральных чисел до множества целых.Множество целых чиселZ
- 10. Дробные числаПри разделе добычи и при измерениях
- 11. Рациональные числаНазвание рациональных чисел произошло от
- 12. Иррациональные числаИстория возникновения иррациональных чисел начинается VII
- 13. Действительные числаМножество иррациональных чисел обозначают символом J.
- 14. Открытие мнимых и комплексных чисел стало восхитительной главой в истории математики.Мнимые и комплексные числа
- 15. Мнимые числаНазвание "мнимые числа" ввел в 1637
- 16. Ещё истории о мнимых и комплексных числах…Этот
- 17. Факт О Карле ГауссеУже в двухлетнем возрасте
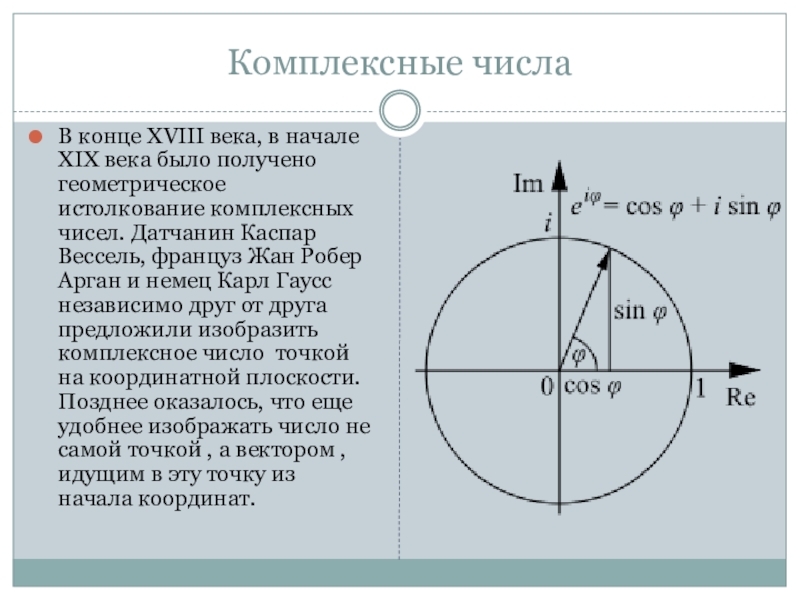
- 18. Комплексные числаВ конце XVIII века, в начале
- 19. Ещё истории о гиперкомплексных числах…После создания теории
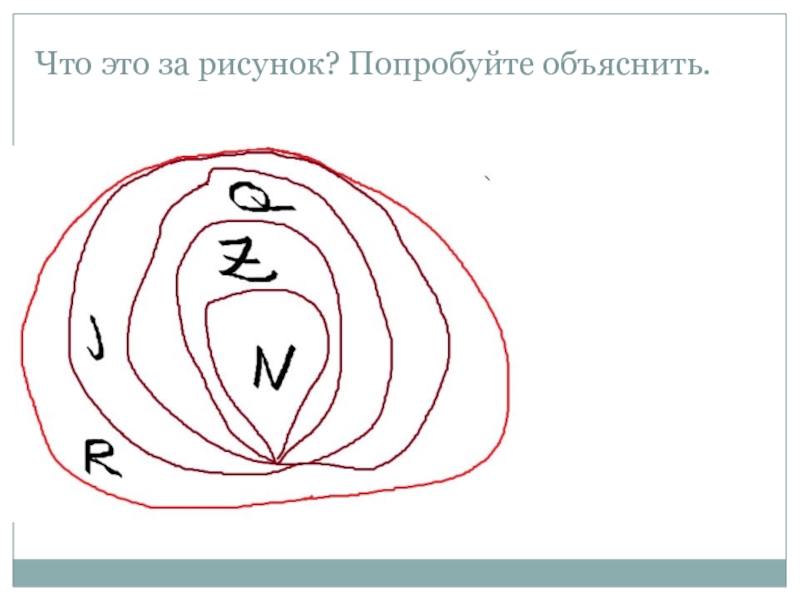
- 20. Что это за рисунок? Попробуйте объяснить.
- 21. Слайд 21
- 22. Спасибо за внимание!
Слайд 3Ответьте на вопросы
Знаете ли вы когда, где и почему возникли числа?
Какие
Хотите ли вы больше узнать о числах?
Слайд 4Немного истории…
Вначале при счете предметов возникли … числа. Их было немного.
Слайд 5Натуральные числа
Никто не знает, когда впервые появились счёт и число.
Но
Ученые полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи-6000 лет назад. А 5000 лет тому назад в Древнем Египте появляются названия для громадных чисел-до миллиона.
охотились на диких животных.
Слайд 6Отрицательные числа
Одним из важнейших этапов в развитии понятия о числе было
И отдельно о числе – нуль (ноль). Ноль, например, назывался словами «пустое», «небо», «дыра»
Диофант Александрийский
Слайд 7Отрицательные числа
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа
Слайд 8Ещё немного из истории отрицательных чисел…
Несмотря на такие сомнения, правила
+ 5 -56
-7 - 33
-0,6
25
15*(-8)
-130: (-13)
17
Слайд 9Ещё истории…
Введение отрицательных чисел и нуля позволило расширить множество натуральных чисел
Множество целых чисел
Z
Слайд 10Дробные числа
При разделе добычи и при измерениях величин люди встретились с
Чтобы облегчить действия с дробями, были придуманы десятичные дроби.
Слайд 11 Рациональные числа
Название рациональных чисел произошло от латинского "ratio" (что в
Другое название рациональных чисел – дроби. Дроби – это числа, которыми можно обозначит нецелое количество определенных предметов (например, полстакана, три четверти пятого, треть лимона и т.д.). Под дробью также понимают те рациональные числа, которые к целым отнести нельзя.
Слайд 12
Иррациональные числа
История возникновения иррациональных чисел начинается VII веке до нашей эры. Индийский
Первое доказательство существования иррациональных чисел обычно связывают с Пифагорейской школой. Иррациональные числа были выявлены при обнаружении сторон пентаграммы.
Противоположен рационализму. ИРРАЦИОНАЛЬНОЕ (от лат. irrationalis — неразумный) находящееся за пределами разума, алогическое, неинтеллектуальное, несоизмеримое с рациональным мышлением или противоречащее ему.
Слайд 13
Действительные числа
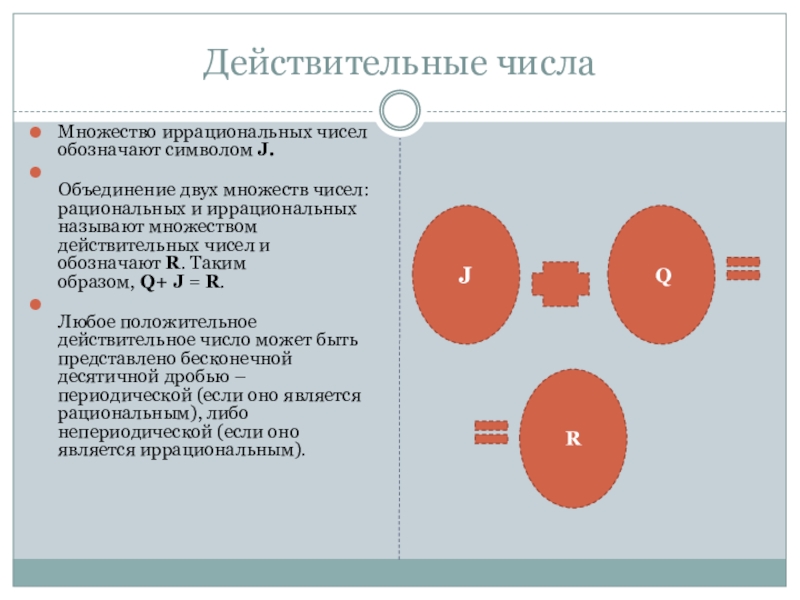
Множество иррациональных чисел обозначают символом J.
Объединение двух множеств чисел: рациональных и
Любое положительное действительное число может быть представлено бесконечной десятичной дробью – периодической (если оно является рациональным), либо непериодической (если оно является иррациональным).
J
Q
R