Презентация, доклад по математике для освоения основ геометрии.

Где домик Пятачка?

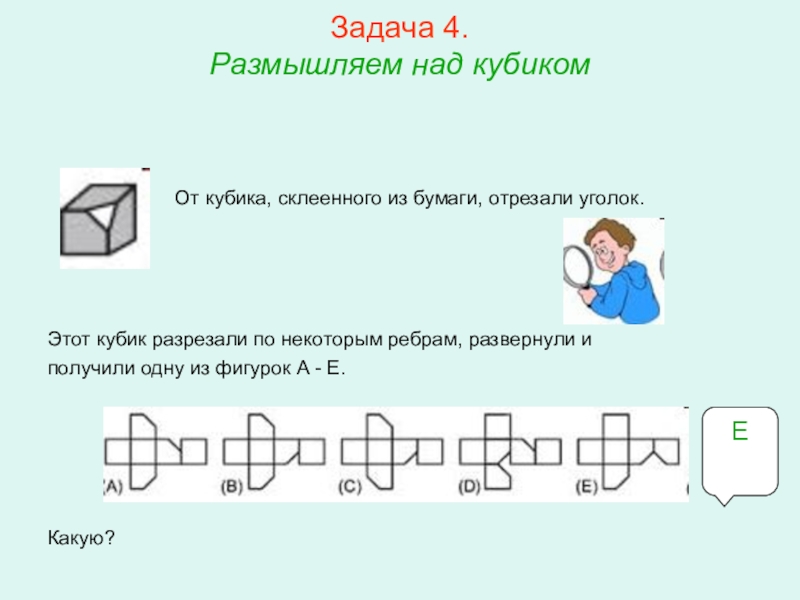
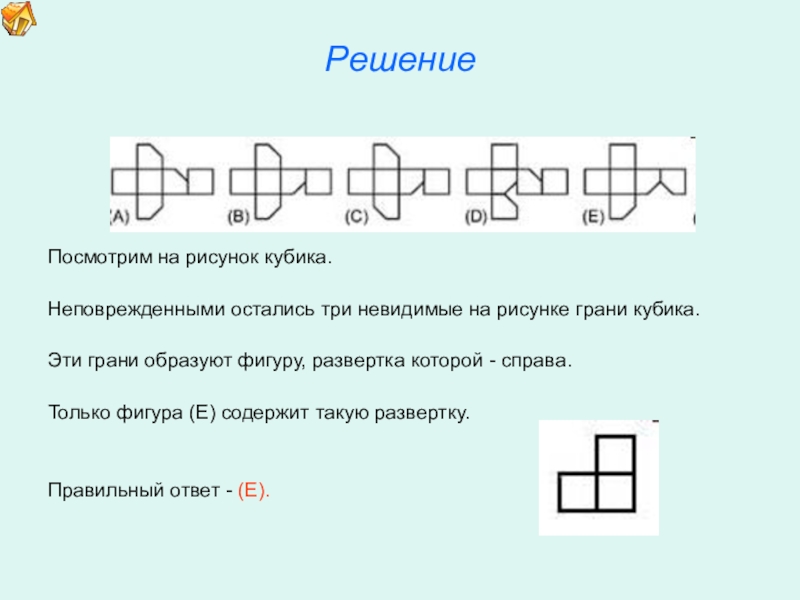
4. Размышляем над кубиком.

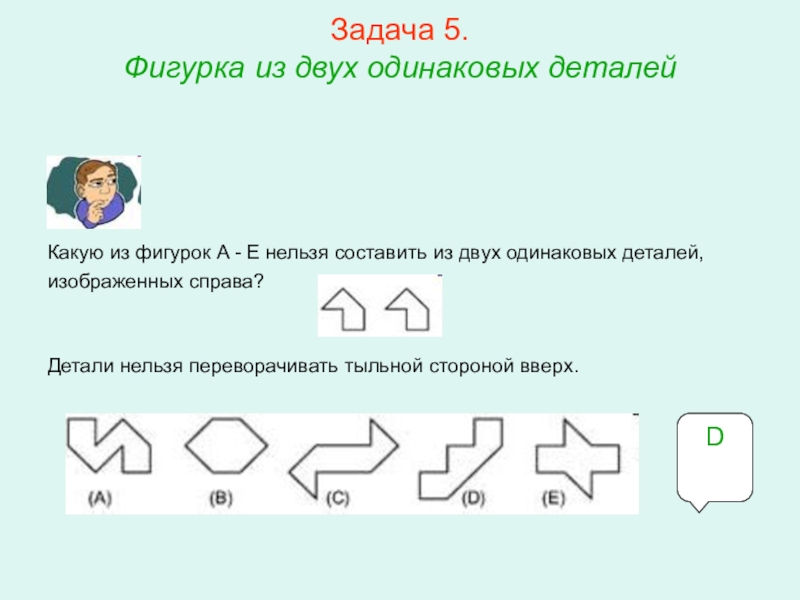
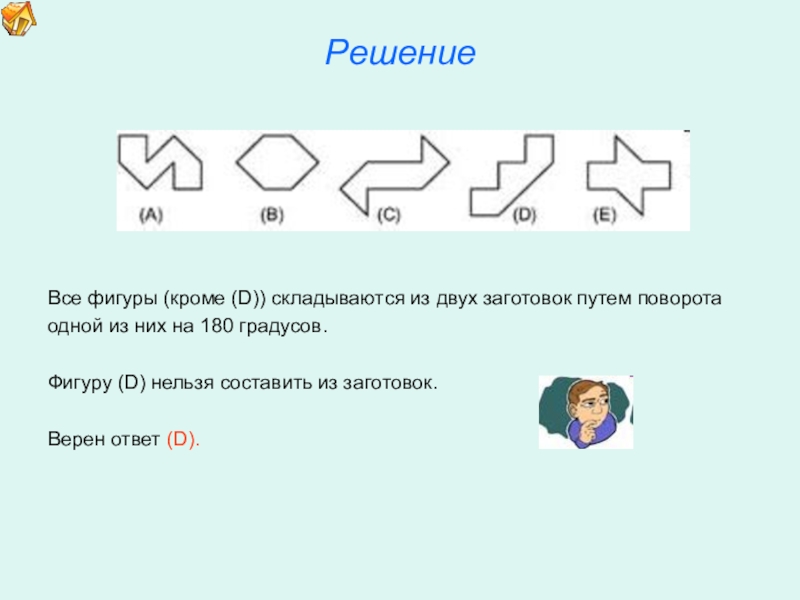
5. Фигурки из двух одинаковых деталей.

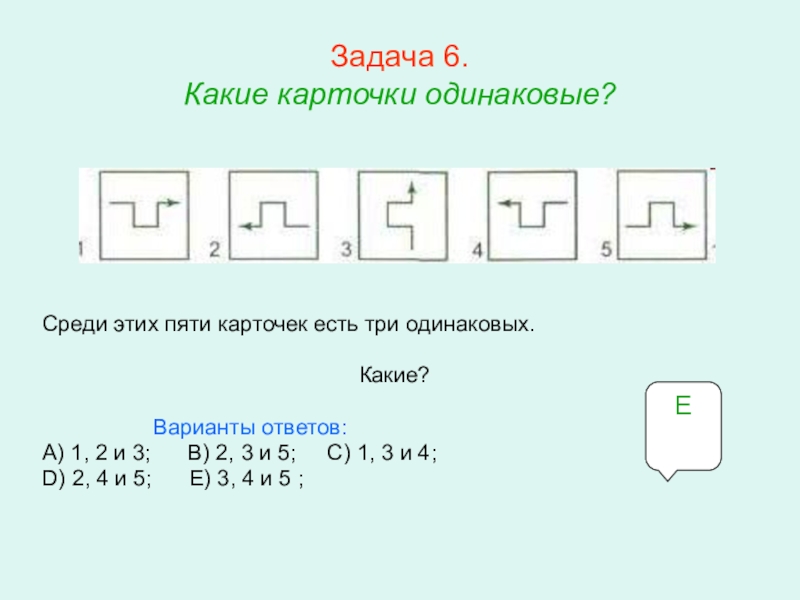
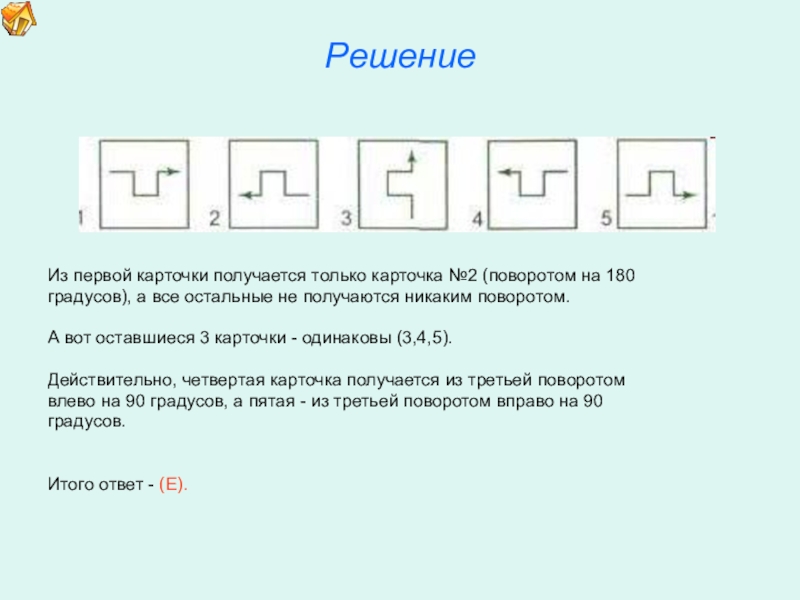
6. Какие карточки одинаковые?

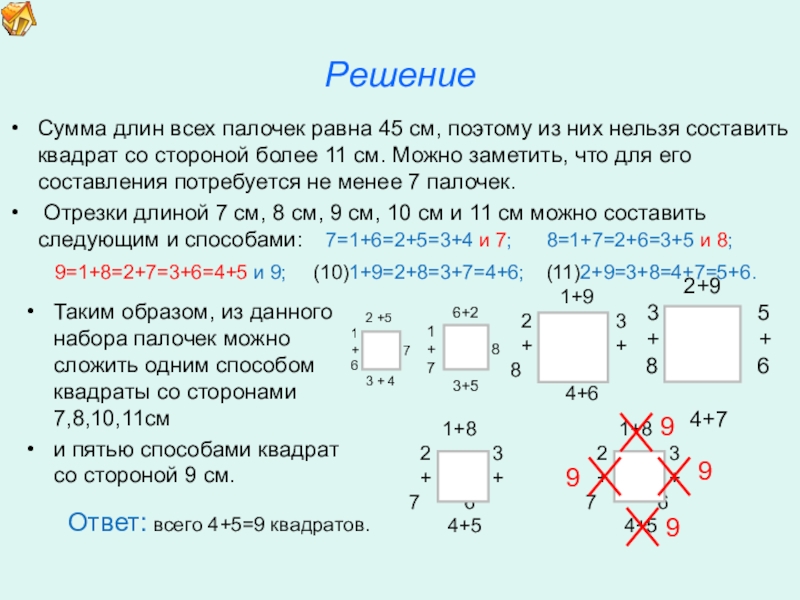
7. Девять палочек.

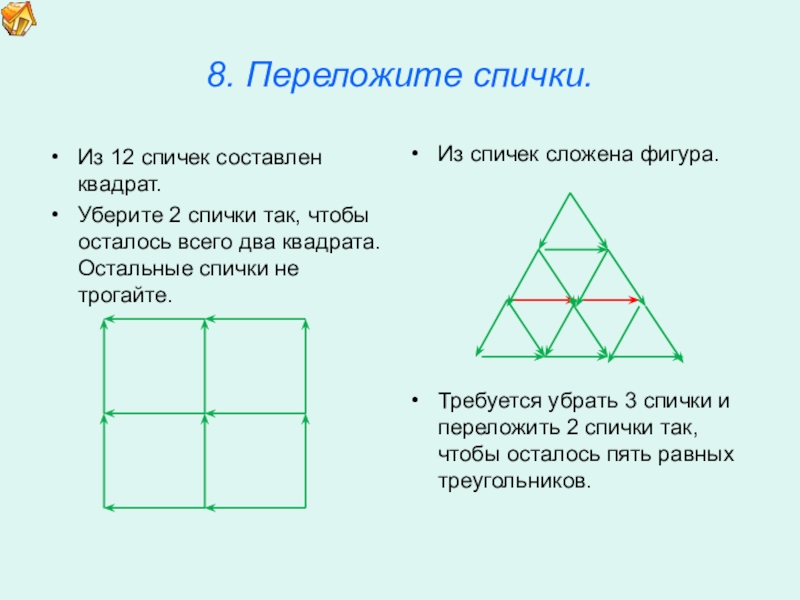
8. Переложите спички.

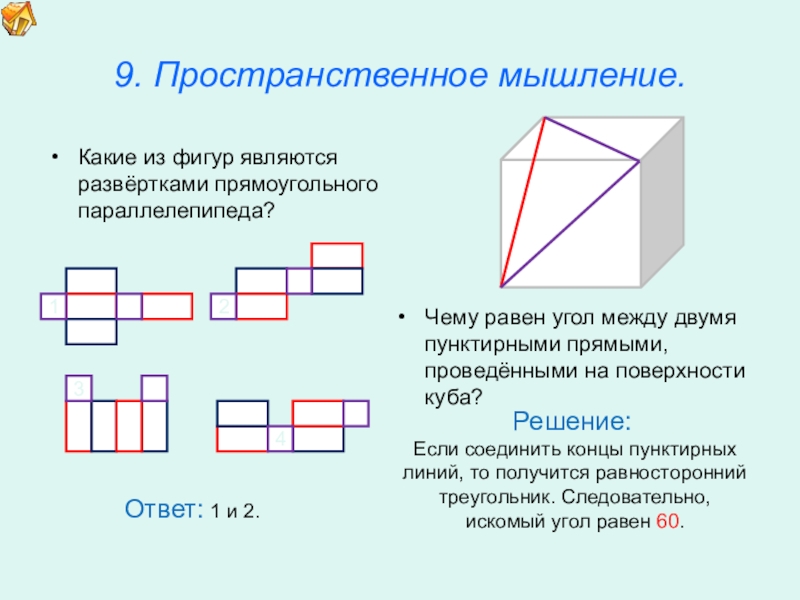
9. Пространственное мышление.

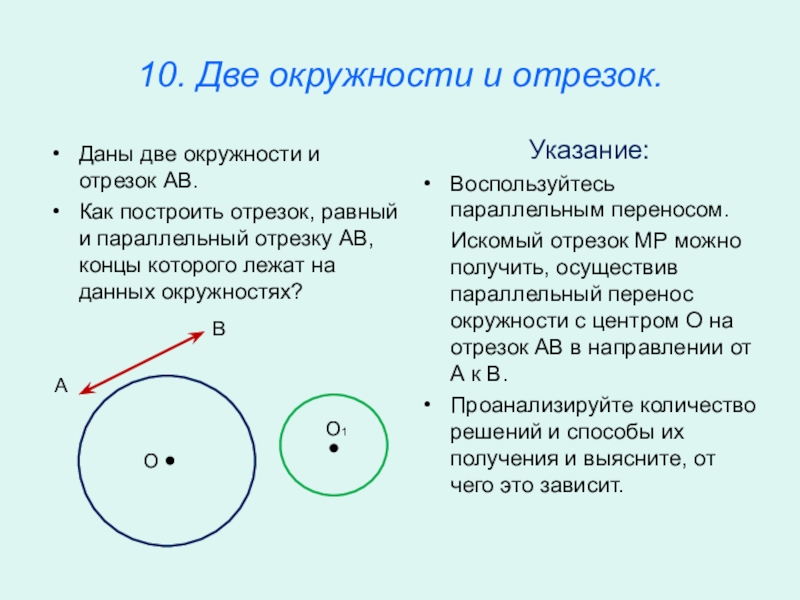
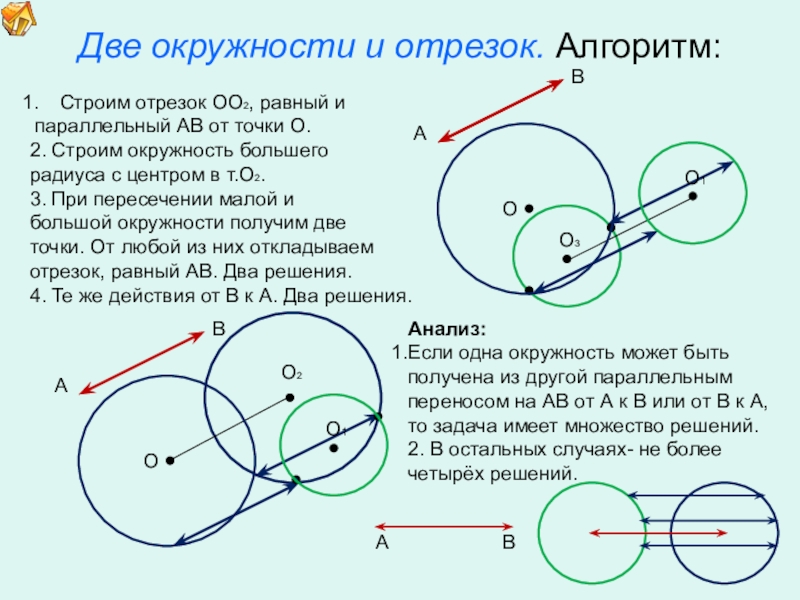
10. Две окружности и отрезок.

11. Всадник выбирает дорогу.

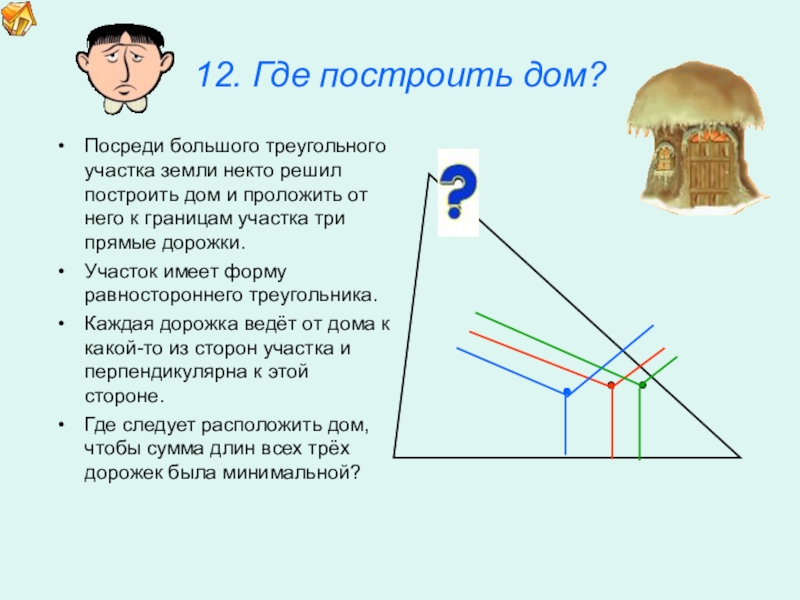
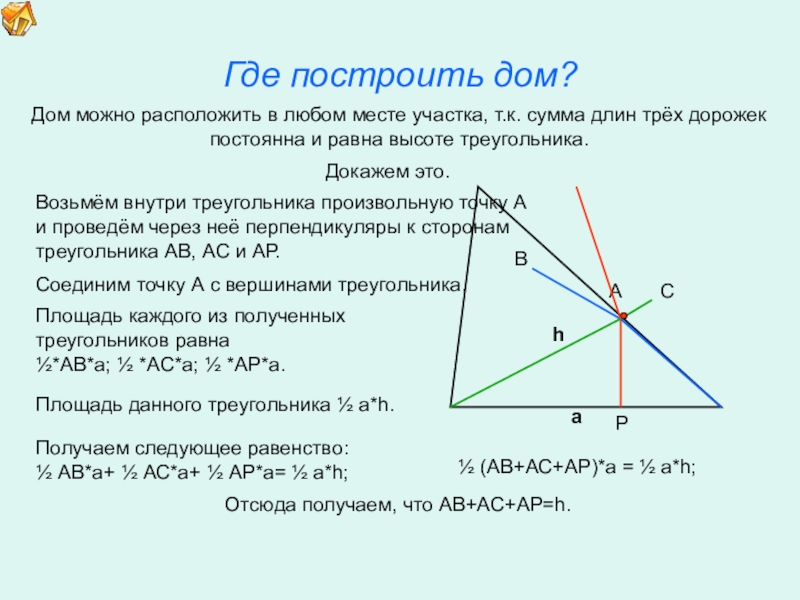
12. Где построить дом?

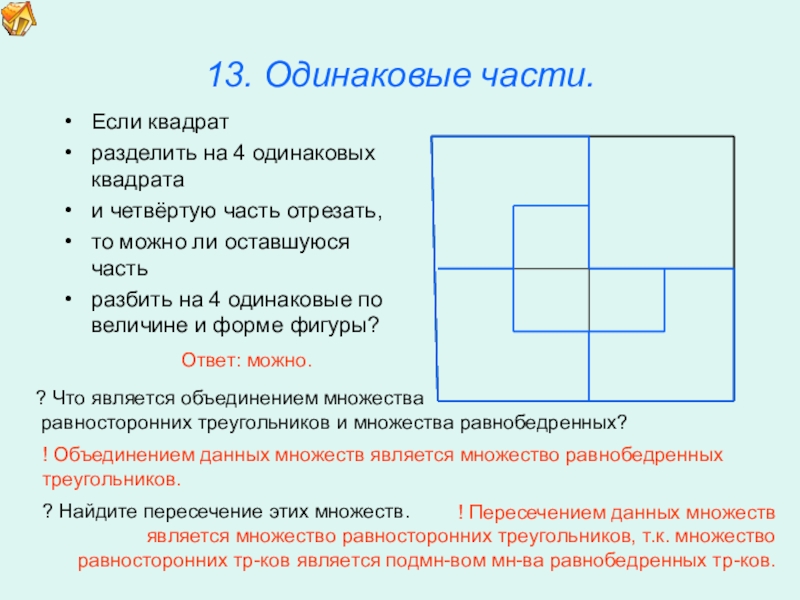
13. Одинаковые части

Подборку задач выполнила учитель математики Руднева Н.В.

объезжать этот участок по запасному пути,
отмеченному на плане пунктиром.

На сколько километров увеличивает путь этот объезд?

Варианты ответов:
A) 3 км;
B) 5 км;
C) 6 км;
D) 10 км;
E) Невозможно определить

С

3 км + 3 км = 6 км.

Ответ - (С).

На каждой грани бумажного кубика написана цифра
1, 2 или 3, причем цифры на противоположных гранях
- одинаковые.








Какая из фигурок может получиться. если этот кубик
разрезать по некоторым ребрам и развернуть?

Е

и 2 являются
противоположными, а это недопустимо по условию задачи.

По развертке (D) видно, что грани с цифрами 1 и 3 - противоположны, то
есть этот вариант тоже не подходит.

Вариант (E) - подходит, так как все противоположные грани помечены
одинаковыми цифрами.


Верен ответ - (Е).

Домик Кролика нарисован 4 раза, а домик Пятачка только
один раз.

Где домик Пятачка?

В

Предположим, что кролик живет в домике (Е). Тогда домик (D) - тот же
домик, но повернут так, что видна левая стенка.

А домик (С), - это домик (Е), если смотреть на него со стороны входа.
Домик (В) - не домик Кролика, так как правая его стена имеет одно окно, а
правая стена от входа домика Кролика ( смотрим на домик (D) ) имеет два
окошка.

А вот домик (А) - домик Кролика: это домик (D), если смотреть на него со
стороны входа.

Итак, у Кролика четыре домика: (А), (С),(D) и (Е), а (В) - домик Пятачка.


Правильный ответ - (В).

От кубика, склеенного из бумаги, отрезали уголок.




Этот кубик разрезали по некоторым ребрам, развернули и
получили одну из фигурок A - E.





Какую?

Е

грани образуют фигуру, развертка которой - справа.

Только фигура (Е) содержит такую развертку.


Правильный ответ - (Е).

E нельзя составить из двух одинаковых деталей,
изображенных справа?


Детали нельзя переворачивать тыльной стороной вверх.

D

них на 180 градусов.

Фигуру (D) нельзя составить из заготовок.

Верен ответ (D).

Варианты ответов:
A) 1, 2 и 3; B) 2, 3 и 5; C) 1, 3 и 4;
D) 2, 4 и 5; E) 3, 4 и 5 ;

Е

все остальные не получаются никаким поворотом.

А вот оставшиеся 3 карточки - одинаковы (3,4,5).

Действительно, четвертая карточка получается из третьей поворотом
влево на 90 градусов, а пятая - из третьей поворотом вправо на 90
градусов.


Итого ответ - (Е).

9 см. Квадраты с какими сторонами и сколькими способами можно составить из этих палочек?

(Не обязательно использовать все палочки,
способы составления одного квадрата считаются разными, если использованы разные палочки).

составить квадрат со стороной более 11 см. Можно заметить, что для его составления потребуется не менее 7 палочек.
Отрезки длиной 7 см, 8 см, 9 см, 10 см и 11 см можно составить следующим и способами:

2+9
3 5
+ +
6

4+7

Ответ: всего 4+5=9 квадратов.

Таким образом, из данного набора палочек можно сложить одним способом квадраты со сторонами 7,8,10,11см
и пятью способами квадрат со стороной 9 см.

7=1+6=2+5=3+4 и 7;

8=1+7=2+6=3+5 и 8;

9=1+8=2+7=3+6=4+5 и 9;

(10)1+9=2+8=3+7=4+6;

(11)2+9=3+8=4+7=5+6.

чтобы осталось всего два квадрата. Остальные спички не трогайте.

Из спичек сложена фигура.







Требуется убрать 3 спички и переложить 2 спички так, чтобы осталось пять равных треугольников.

между двумя пунктирными прямыми, проведёнными на поверхности куба?

Решение:
Если соединить концы пунктирных
линий, то получится равносторонний
треугольник. Следовательно,
искомый угол равен 60.

Ответ: 1 и 2.

МР можно получить, осуществив параллельный перенос окружности с центром О на отрезок АВ в направлении от А к В.
Проанализируйте количество решений и способы их получения и выясните, от чего это зависит.

Даны две окружности и отрезок АВ.
Как построить отрезок, равный и параллельный отрезку АВ, концы которого лежат на данных окружностях?

от точки О.
2. Строим окружность большего
радиуса с центром в т.О2.
3. При пересечении малой и
большой окружности получим две
точки. От любой из них откладываем
отрезок, равный АВ. Два решения.
4. Те же действия от В к А. Два решения.

Анализ:
Если одна окружность может быть
получена из другой параллельным
переносом на АВ от А к В или от В к А,
то задача имеет множество решений.
2. В остальных случаях- не более
четырёх решений.

О2

О3

Всадник из пункта М (М - внутри угла АСВ) должен по возможности скорее добраться до дороги СА, чтобы с попутной машиной передать письмо, но при этом сначала ему нужно напоить коня в реке СВ.
Как он должен ехать?

А

С

В

М

перпендикулярна СВ.
Затем проведём РН перпендикулярно СА. Пересечение НР и СВ даёт точку Д.
Искомый путь МДН.

М

С

А

В

К

Н

Путь МДН будет кратчайшим.
Действительно, для любой точки Х,
взятой на луче СВ, имеем: длина
ломаной МХУ равна длине ломаной РХУ,
но длина ломаной РХУ больше длины
отрезка НР, т.к. НД=УЕ, а РД меньше ЕР.

У

Х

Построение:

Доказательство:

Д

дом и проложить от него к границам участка три прямые дорожки.
Участок имеет форму равностороннего треугольника.
Каждая дорожка ведёт от дома к какой-то из сторон участка и перпендикулярна к этой стороне.
Где следует расположить дом, чтобы сумма длин всех трёх дорожек была минимальной?

длин трёх дорожек
постоянна и равна высоте треугольника.

а

Докажем это.

Соединим точку А с вершинами треугольника.

Площадь каждого из полученных
треугольников равна
½*АВ*а; ½ *АС*а; ½ *АР*а.

Площадь данного треугольника ½ а*h.

Получаем следующее равенство:
½ АВ*а+ ½ АС*а+ ½ АР*а= ½ а*h;

½ (АВ+АС+АР)*а = ½ а*h;

Отсюда получаем, что АВ+АС+АР=h.

Возьмём внутри треугольника произвольную точку А
и проведём через неё перпендикуляры к сторонам
треугольника АВ, АС и АР.

часть отрезать,
то можно ли оставшуюся часть
разбить на 4 одинаковые по величине и форме фигуры?

Ответ: можно.

? Что является объединением множества
равносторонних треугольников и множества равнобедренных?

? Найдите пересечение этих множеств.

! Объединением данных множеств является множество равнобедренных
треугольников.

! Пересечением данных множеств
является множество равносторонних треугольников, т.к. множество
равносторонних тр-ков является подмн-вом мн-ва равнобедренных тр-ков.