- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Десять способов решения квадратного уравнения
Содержание
- 1. Презентация по математике Десять способов решения квадратного уравнения
- 2. ГипотезаСуществует оптимальный способ решения квадратных уравнений – это решение уравнений по формулам, изучаемых в школьной программе
- 3. Цель работы Расширить представление о квадратных уравнениях
- 4. Предмет исследования: квадратные уравнения.Объект исследования: способы решения квадратных уравнений.Метод исследования: аналитический
- 5. План работыИстория развития квадратных уравнений
- 6. История развития квадратных уравнений.Квадратные уравнения в Древнем
- 7. Как составлял и решал Диофант квадратные уравнения
- 8. Как решал квадратные уравнения Ал-Хорезми?Учебник математики
- 9. Узбекский математик, поэт и врач Омар Хайям
- 10. Квадратные уравнения в Европе XIII—XVII веков
- 11. Михаэль ШтифельОбщее правило решения квадратных уравнений, приведенных
- 12. Франсуа ВиетБлагодаря трудам Виета
- 13. Рене Декарт«Алгебраические обозначения получают усовершенствование у Виета
- 14. Эти ученые внесли достойный вклад в развитие
- 15. Способы решения квадратных уравнений.
- 16. 1 СПОСОБ: Разложение левой части уравнения на
- 17. 2 СПОСОБ: Метод выделения полного квадрата.Решим
- 18. 3 СПОСОБРешение квадратных уравнений по формуле.ах2 + bх + с = 0,
- 19. 4 СПОСОБ Решение уравнений с использованием теоремы
- 20. 5 СПОСОБ Решение уравнений способом «переброски».ах2 +
- 21. 6 СПОСОБ Свойства коэффициентов квадратного уравнения.Пусть дано
- 22. 7 СПОСОБГрафическое решение квадратного уравнения.х2 + px
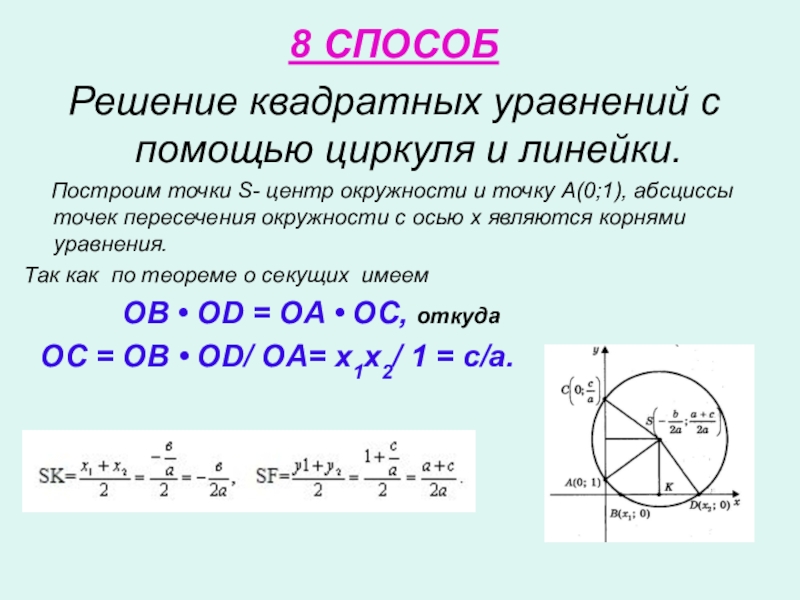
- 23. 8 СПОСОБ Решение квадратных уравнений с помощью
- 24. 1) Радиус окружности больше ординаты центра (AS
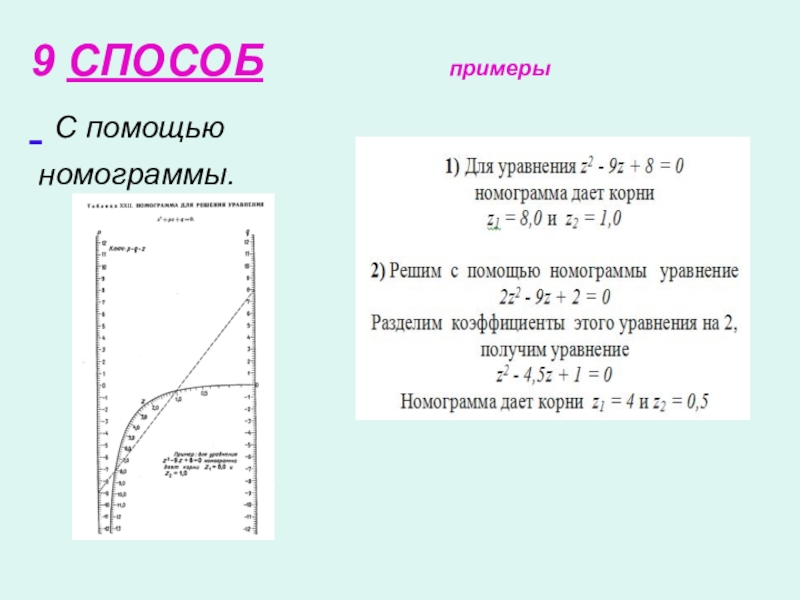
- 25. 9 СПОСОБ примеры С помощью номограммы.
- 26. 10 СПОСОБ Геометрический способ решения квадратных уравнений.
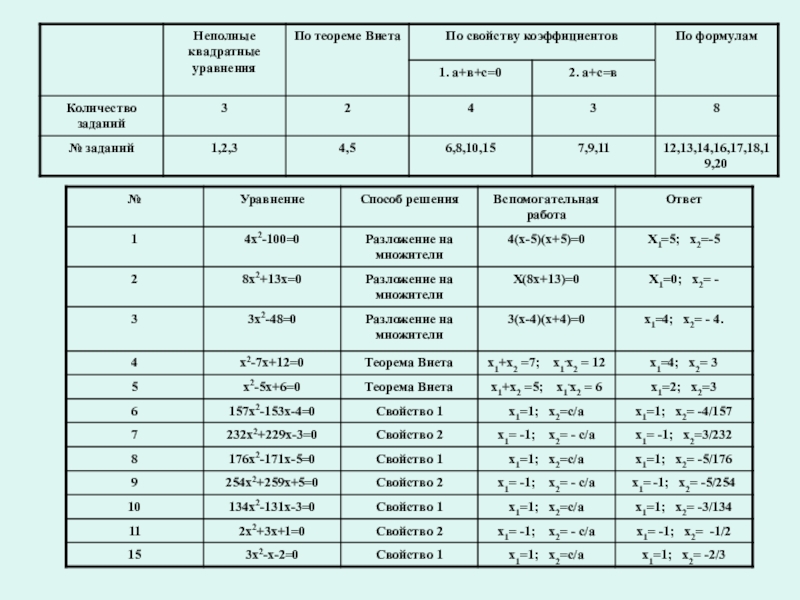
- 27. Исследовательская работа по нахождению оптимальных способов
- 28. Слайд 28
- 29. Слайд 29
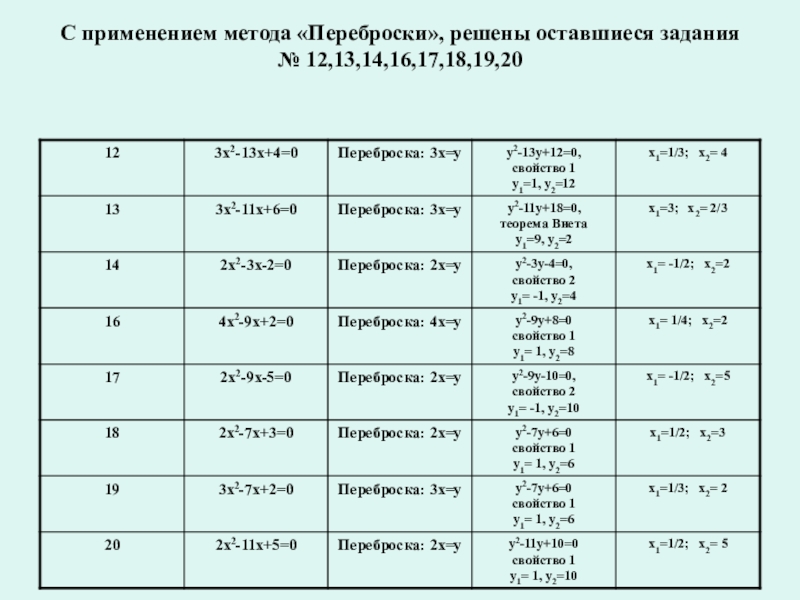
- 30. С применением метода «Переброски», решены оставшиеся задания № 12,13,14,16,17,18,19,20
- 31. Для сравнения: на одно задание теста
- 32. Выводы:Развитие науки
- 33. Список литературы1. Макарычев Ю.Н.,Миндюк Н.Г., Нешков К.И.,Алгебра,
Слайд 110 способов решения квадратных уравнений
Выполнил:
Ученик 9 А класса
МОБУ СОШ№1 Ковалёв
Учитель Авдеева Л.Н.
Слайд 2Гипотеза
Существует оптимальный способ решения квадратных уравнений – это решение уравнений по
Слайд 3Цель работы
Расширить представление о квадратных уравнениях
Задачи:
Познакомиться с информацией о решении уравнений
Изучить различные способы решения квадратных уравнений
Слайд 4Предмет исследования:
квадратные уравнения.
Объект исследования:
способы решения квадратных уравнений.
Метод исследования:
аналитический
Слайд 5План работы
История развития квадратных уравнений
4 Квадратные уравнения и Омар Хайям 5. Квадратные уравнения в Европе XIII - XVII вв 6. О теореме Виета
Способы решения квадратных уравнений
1. Разложение левой части уравнения на множители 2. Метод выделения полного квадрата
3. Решение квадратных уравнений по формуле
4. По теореме Виета
5. Способ «переброски»
6. По свойствам коэффициентов
7. Графическое решение
8. С помощью циркуля и линейки
9. С помощью номограммы
10. Геометрический способ
Заключение
Исследования и выводы.
Слайд 6История развития квадратных уравнений.
Квадратные уравнения в Древнем Вавилоне:
Неполные квадратные
Об этом свидетельствуют найденные клинописные тексты задач с решениями в виде уравнений.
Слайд 7Как составлял и решал Диофант квадратные уравнения
«Найти два числа, зная,
(10+х)(10-х) =96
или же:
100 - х2 =96
х2 - 4=0
Решение х= -2 для Диофанта не
существует так как греческая математика
Знала только положительные числа.
Слайд 8Как решал квадратные уравнения
Ал-Хорезми?
Учебник математики Ал-Хорезми,
выпущенный им около 830 года
„Китаб аль-джебр валь мукабала", посвящен
в основном решению уравнений первой и второй
степени. Этот математик уравнения решает также
геометрически. Вот пример, ставший знаменитым,
из «Алгебры» ал - Хорезми: х2 +10х = 39.
В оригинале эта задача формулируется следующим
образом: «Квадрат и десять корней равны 39».
Слайд 9Узбекский математик, поэт и врач
Омар Хайям уже в IX веке
Систематически изучил уравнения
третьей степени, дал их классификацию,
выяснил условия их разрешимости
(в смысле существования положительных
корней). Хайям в своём алгебраическом
трактате говорит, что он много
занимался поисками точного решения
уравнений третьей степени.
Омар Хайям
Слайд 10Квадратные уравнения в Европе
XIII—XVII веков
Способы решения квадратных уравнений
Слайд 11Михаэль Штифель
Общее правило решения
квадратных уравнений,
приведенных к виду
при всевозможных комбинациях
знаков коэффициентов b, с
было сформулировано в Европе
лишь в 1544 г.
немецким математиком
Михаэлем Штифелем.
Слайд 12Франсуа Виет
Благодаря трудам Виета открылась возможность выражения свойств
Впервые свои исследования по математике Виет опубликовал в книге "Математический канон" в 1574 году. Эта книга печаталась за счет Виета и поэтому вышла очень небольшим тиражом. Его работы были написаны столь трудным для понимания математическим языком, что не нашли такого распространения, которого заслуживали. Все свои математические труды Виет опубликовал в 1591 году в книге „Isagoge in artem analiti-cam". Они свидетельствовали о всесторонности его знаний.
Спустя 40 лет после смерти Виета его произведения были изданы под общим заглавием “Opera mathematica”.
Слайд 13Рене Декарт
«Алгебраические обозначения получают усовершенствование
у Виета и Декарта; начиная с
Андронов А.А.,
советский математик
Слайд 14Эти ученые внесли достойный вклад в развитие теории
Франсуа Виет (1540 – 1603, Франция) вывел формулы решения квадратного уравнения в общем виде, однако он признавал только положительные числа.
Штифель (1486 – 1567, Германия) в 1544 году сформировал общее правило решения квадратных уравнений, приведённых к единому каноническому виду х2 + b x = c при всевозможных комбинациях знаков и коэффициентов b и c.
Итальянские учёные Тарталья (1500-1557), Кардано (1501-1576), Бомбелли (1526-1572) среди первых в XVI веке учитывают, помимо положительных, и отрицательные корни.
В XVII веке благодаря трудам Жирара (1595-1632, Голландия), Декарта (1596-1650, Франция), Ньютона (1643-1727, Англия) и других учёных, способ решения квадратных уравнений принимает современный вид.
Слайд 161 СПОСОБ:
Разложение левой части уравнения на множители.
х2 + 10х
Разложим левую часть на множители способом группировки:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере,
один из его множителей равен нулю.
Это означает
2 и -12
корни уравнения
х2 + 10х - 24 = 0.
Слайд 172 СПОСОБ:
Метод выделения полного квадрата.
Решим уравнение
х2 + 6х
выделив в левой части полный квадрат.
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 =
(х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0
(х + 3)2 = 16.
х + 3 - 4 = 0 или х+ 3 = -4,
х1 = 1 х2 = -7.
Слайд 194 СПОСОБ
Решение уравнений с использованием теоремы Виета.
Для приведённого уравнения
х2 +
x1 x2 = q,
x1 + x2 = - p
Для полного уравнения
ах2 + вx + с = 0.
x1 x2 = с/а,
x1 + x2 = - в/а
Слайд 205 СПОСОБ
Решение уравнений способом «переброски».
ах2 + bх + с =
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Замена ах = у, откуда х = у/а;
Уравнение у2 + by + ас = 0 равносильно данному.
Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х1 = у2/а.
Слайд 216 СПОСОБ
Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение
ах2 +
Если, а + b + с = 0 , то х1 = 1, х2 = с/а.
Если, а + с = в , то х1 = -1, х2 = - с/а.
Слайд 22
7 СПОСОБ
Графическое решение квадратного уравнения.
х2 + px + q = 0
Перенесём
правую часть уравнения
х2 = - px - q.
Построим графики функций
у = х2 и у = - px - q.
Точки пересечения графиков
являются корнями уравнения
Слайд 238 СПОСОБ
Решение квадратных уравнений с помощью циркуля и линейки.
Так как по теореме о секущих имеем
OB • OD = OA • OC, откуда
OC = OB • OD/ OA= х1х2/ 1 = c/a.
Слайд 241) Радиус окружности больше ординаты центра
(AS > SK, или R
( рис.1) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения
ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра
(AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 2) в точке В(х1; 0), где х1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис.3), в этом случае уравнение не имеет решения.
рис.1 рис.2 рис.3
Слайд 2610 СПОСОБ
Геометрический способ решения квадратных уравнений.
х2 + 10x = 39
В оригинале эта задача формулируется
следующим образом :
«Квадрат и десять корней равны 39»
Слайд 27Исследовательская работа по нахождению оптимальных способов решения тематического теста «Решение уравнений второй степени
Слайд 31Для сравнения: на одно задание теста с № 6 по 10
Слайд 32
Выводы:
Развитие науки о решении квадратных уравнений
Только после трудов Штифеля, Виета, Тартальи, Кардано, Бомбелли, Жирара, Декарта, Ньютона наука о решении квадратных уравнений приняла современный вид.
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры, они играют огромную роль в развитии математики.
Знание способов решения квадратных уравнений позволит мне выбирать рациональный в каждом конкретном случае, сэкономит время решения при применении свойств коэффициентов или теоремы Виета.
Слайд 33Список литературы
1. Макарычев Ю.Н.,Миндюк Н.Г., Нешков К.И.,Алгебра, 8 кл.,М., «Мнемозина».
2. Брадис
Изд. 57-е. - М., Просвещение, 1990. С. 83.
3. С.В.Шиловская, За страницами учебника (открытые уроки, математические кружки, подготовка к олимпиадам),-М: Глобус,2008,с.76-82.
4. Литвинова С.А., Куликова и др. За страницами учебника (открытые уроки, математические кружки, подготовка к олимпиадам), Решение алгебраических задач геометрическим методом, -М: Глобус,2008,с.35-38.
5. Энциклопедический словарь юного математика для среднего и старшего школьного возраста, М., «Педагогика»,1985.
6. Попова И.Н. Учебно- тренировачные и тематические тесты по математике, Базовый уровень. 9 класс. Государственная итоговая аттестация в новой форме.