- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 6 класс на тему Прямая и обратная пропорциональность
Содержание
- 1. Презентация по математике 6 класс на тему Прямая и обратная пропорциональность
- 2. Повторим!!!Что такое пропорция?Прочитайте пропорцию х:а=у:в.Назовите ее крайние
- 3. Устно решить задачи!!!1)Найдите неизвестный член пропорции 5:х=4:12.2)Верна
- 4. Устно решить задачи!!!5)Станок за 2 часа изготавливает
- 5. ЗАДАЧА 1Сколько нужно сахара, чтобы сварить варенье
- 6. Решение:1) 5:4=1,25 (кг) – нужно сахара на
- 7. II способ Алгоритм решения задач на пропорции1)
- 8. 4 кг ягод5 кг сахара10 кг ягодx
- 9. Устно решить задачи!!!5)Станок за 2 часа изготавливает
- 10. ДВЕ ВЕЛИЧИНЫ НАЗЫВАЮТСЯ ПРЯМО ПРОПОРЦИОНАЛЬНЫМИ, ЕСЛИ ПРИ
- 11. Задача №2 Ученик 6 класса
- 12. Решение задачи №21)Пусть x дн.потребуется,чтобы съесть 30
- 13. Задача №3Площадь поля
- 14. Слайд 14
- 15. Обратно пропорциональные величиныДве величины называют обратно пропорциональными,
- 16. Не пропорциональные величины Не всякие две
- 17. №3.Рабочие бригады, состоящей из 8 человек, могут
- 18. Слайд 18
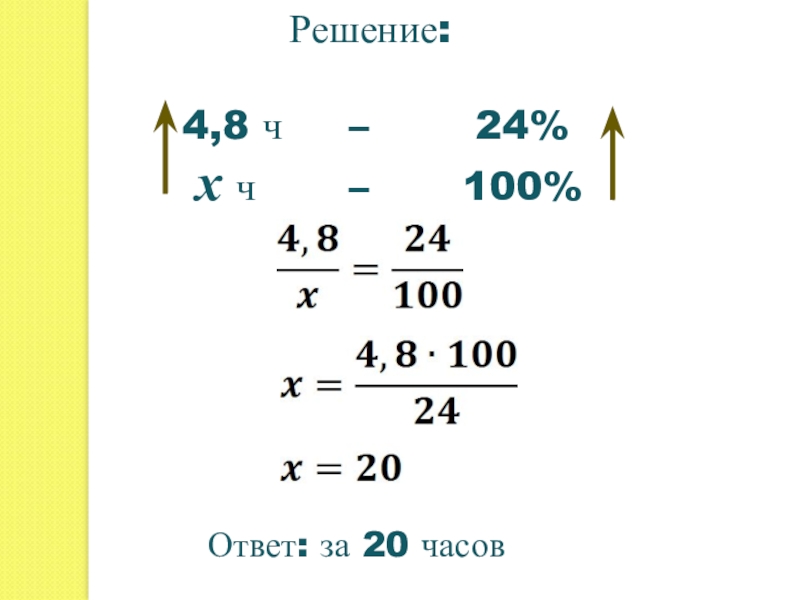
- 19. №5.Вновь выстроенный бассейн необходимо заполнить морской водой.
- 20. Решение:4,8 ч
- 21. Закрепление материала:№ 783, 784, 794, 803 (а,б)Домашнее задание:§22(прямая пропорциональная зависимость), № 811,813
Слайд 2Повторим!!!
Что такое пропорция?
Прочитайте пропорцию х:а=у:в.
Назовите ее крайние члены; средние члены.
Сформулируйте основное
Какие перестановки членов пропорции снова приводят к верным пропорциям?
Слайд 3Устно решить задачи!!!
1)Найдите неизвестный член пропорции 5:х=4:12.
2)Верна ли пропорция: 12:0,2=30:0,5?
3)Автобус был
4)Как зависит путь от времени движения автобуса?
Х=15
Да
240км
Чем больше времени едет автобус,
тем больший путь он проедет.
Слайд 4Устно решить задачи!!!
5)Станок за 2 часа изготавливает 28 деталей. Сколько деталей
6)Как зависит количество деталей от времени работы станка?
Такие величины, как время движения автобуса и его путь, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
56 деталей
Чем больше времени работает станок,
тем больше деталей он изготовит.
Слайд 5ЗАДАЧА 1
Сколько нужно сахара, чтобы сварить варенье из 10 кг клубники,
Запишем решение I способом:
Слайд 6Решение:
1) 5:4=1,25 (кг) – нужно сахара на 1кг ягод.
2) 1,25*10=12,5 (кг)
Ответ: 12,5 кг сахара.
Слайд 7II способ
Алгоритм решения задач на пропорции
1) Искомую величину обозначить за x.
2)
3) Указать вид зависимости, поставив стрелочки (в одном направлении, если прямая пропорц. зависимость, в разных, если обратная пропорц. зависимость).
4) Записать пропорцию, следуя по стрелочкам.
5) Решить пропорцию.
6) Записать ответ.
Слайд 84 кг ягод
5 кг сахара
10 кг ягод
x кг сахара
x=(10∙5):4
x=12,5
Ответ:12,5 кг
II способ:
Запишем
Пусть х кг – нужно сахара на 10 кг ягод.
2)
3) Прямая пропорциональная зависимость.
4)
Слайд 9Устно решить задачи!!!
5)Станок за 2 часа изготавливает 28 деталей. Сколько деталей
6)Как зависит количество деталей от времени работы станка?
Такие величины, как время движения автобуса и его путь, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
56 деталей
Чем больше времени работает станок,
тем больше деталей он изготовит.
Слайд 10ДВЕ ВЕЛИЧИНЫ НАЗЫВАЮТСЯ ПРЯМО ПРОПОРЦИОНАЛЬНЫМИ, ЕСЛИ ПРИ УВЕЛИЧЕНИИ (УМЕНЬШЕНИИ) ОДНОЙ ИЗ
ЕСЛИ ДВЕ ВЕЛИЧИНЫ ПРЯМО ПРОПОРЦИОНАЛЬНЫ, ТО ОТНОШЕНИЯ СООТВЕТСТВУЮЩИХ ЗНАЧЕНИЙ ЭТИХ ВЕЛИЧИН РАВНЫ.
Слайд 11
Задача №2
Ученик 6 класса за 5 дней съедает
Слайд 12Решение задачи №2
1)Пусть x дн.потребуется,чтобы съесть 30 кг яблок
2) 5дн.–
х дн. – 30 кг
3) Прямая пропорциональная зависимость.
4)5:х= 1,5:30
x =(5*30):1,5
Х = 100
Ответ: потребуется 100 дней.
Слайд 13 Задача №3
Площадь поля 80 га. Кукурузой засеяли
Слайд 14
1) Пусть х га засеяли кукурузой
2) 80 га-100%
х га-45%
80:х=100:45
Х = (80* 45) :100
Х = 36 (га)
Ответ: 36 га засеяно кукурузой.
Слайд 15Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (уменьшении)
Если две величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.
Слайд 16Не пропорциональные величины
Не всякие две величины являются прямо пропорциональными
Слайд 17
№3.
Рабочие бригады, состоящей из 8 человек, могут выложить бассейн плиткой за
(Производительность бригад одинакова)
Слайд 18
1) 6 – 2 = 4 (дня) время работы второй бригады
2) 8 человек – 6 дней
х человек – 4 дня
Ответ: 12 человек