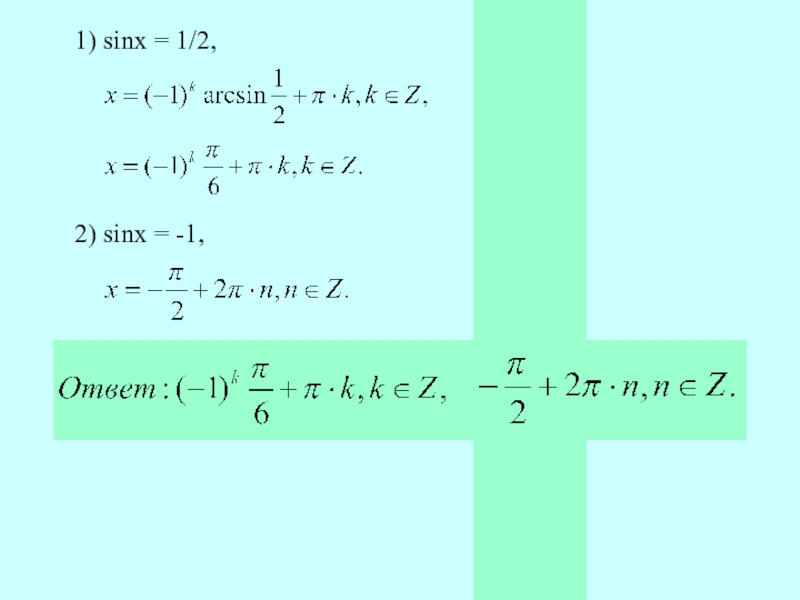- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 1 курс СПО,НПО на тему Тригонометрические уравнения
Содержание
- 1. Презентация по математике 1 курс СПО,НПО на тему Тригонометрические уравнения
- 2. Верно ли, что:
- 3. Имеют ли смысл выражения:
- 4. Решить уравнение:
- 5. Пример 1. Решить уравнение
- 6. 1) sinx = 1/2, 2) sinx = -1,
- 7. Решение.Заменяя sin2x на 1-сos2x, получим квадратное уравнение
- 8. Cледовательно, сos x = - 1/2 или
- 9. Пример 3. Решить уравнение
- 10. t2 - 3t + 2 = 0.По
- 11. Пример 4. sin2 4x
- 12. Пример 5. 3 sin x +4 cos
Слайд 5Пример 1. Решить уравнение
Решение.
Введём новую переменную t = sinx. Тогда данное уравнение примет вид 2t2 + t - 1 = 0.
Решим его: D = 1 + 8 = 9,
Cледовательно,
sinx = 1/2 или sinx = -1.
Слайд 7Решение.
Заменяя sin2x на 1-сos2x, получим квадратное уравнение относительно сosx.
6 (
-6 cos2x + 5cosx + 4 = 0,
6 cos2x - 5cosx - 4 = 0.
Пусть cos x = t, тогда 6t2 - 5t - 4 = 0,
t1= - 1/2, t2 = 4/3.
Слайд 8
Cледовательно, сos x = - 1/2 или cos x = 4/3.
Уравнение
Решая уравнение сos x = -1/2, находим:
Слайд 9Пример 3. Решить уравнение
то уравнение можно записать в виде:
Обозначим tgx через t. Получим уравнение
которое приводится к квадратному t2 - 3t + 2 = 0,
Слайд 12Пример 5. 3 sin x +4 cos x =0;
Решение.
Поделим обе части
3 tg x + 4 =0 ;
tg x = -4/3 ;