- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по матемактике кружок Веселая математика 2019г
Содержание
- 1. Презентация по матемактике кружок Веселая математика 2019г
- 2. Искать решение задач на разрезание ученые начали
- 3. Местный торговец земельными участками отхватил по случаю
- 4. Слайд 4
- 5. ИСТОРИЧЕСКАЯ СПРАВКАПервые попытки к решению были разработаны
- 6. Но систематизировать подход к решению задач на
- 7. Абу-л-ВафаИранский учёныйВикипедияПерсидский учёный X века, один из
- 8. В конце XX века ученые вновь занялись
- 9. Эта пословица предостерегает Вас от поспешности в
- 10. №2 Квадрат состоит из 16 одинаковых клеток,4
- 11. №3 Разрежьте прямоугольник на 4 равные части,
- 12. №3-1 1 способ (4)
- 13. №3-2 2 способ (4)
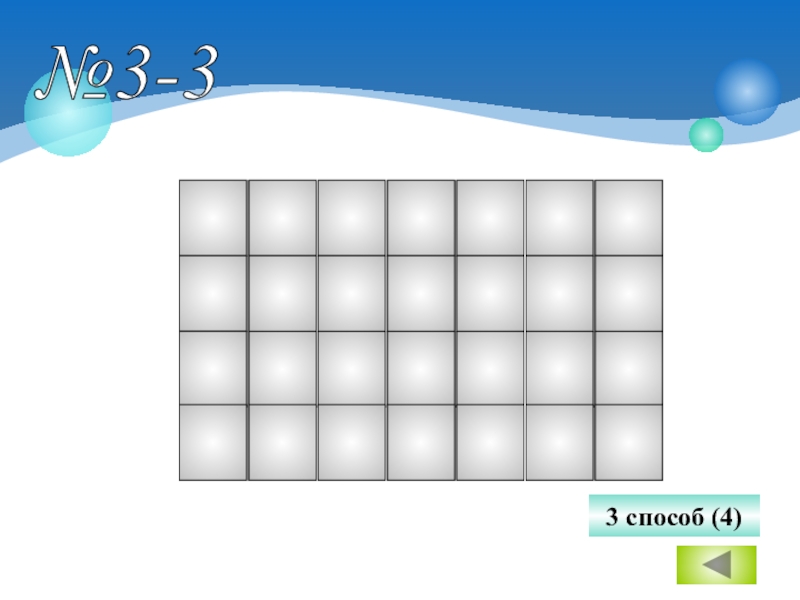
- 14. №3-3 3 способ (4)
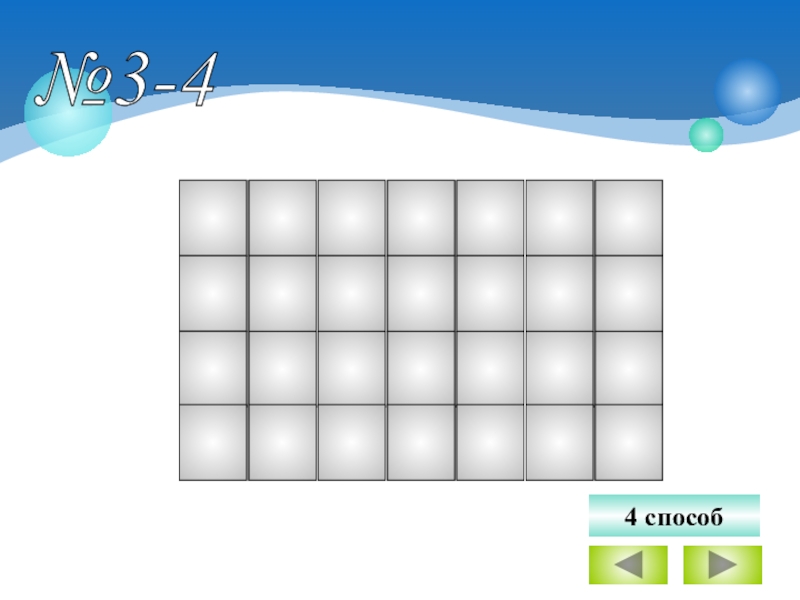
- 15. №3-4 4 способ
- 16. Попробуйте разрезать изображенную на рисунке фигуру на
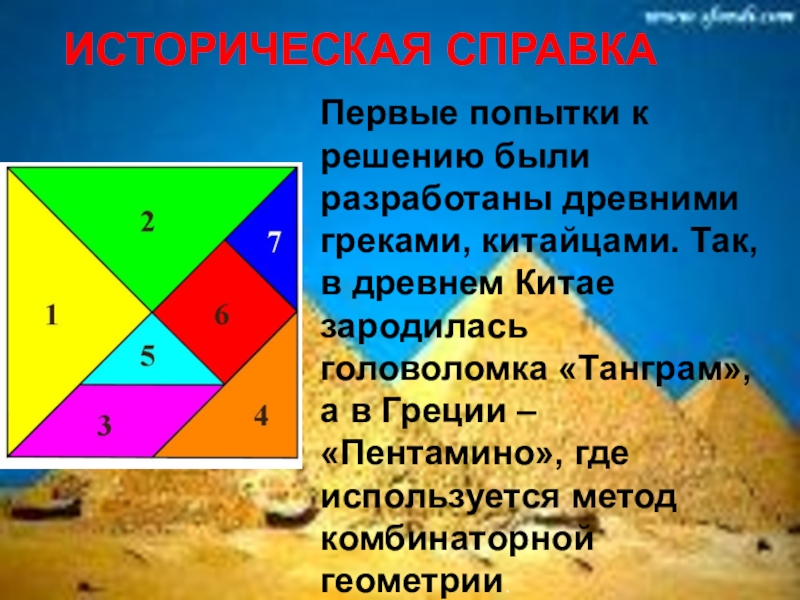
- 17. В Греции появилась головоломка «Пентамино», где используется метод комбинаторной геометрии.
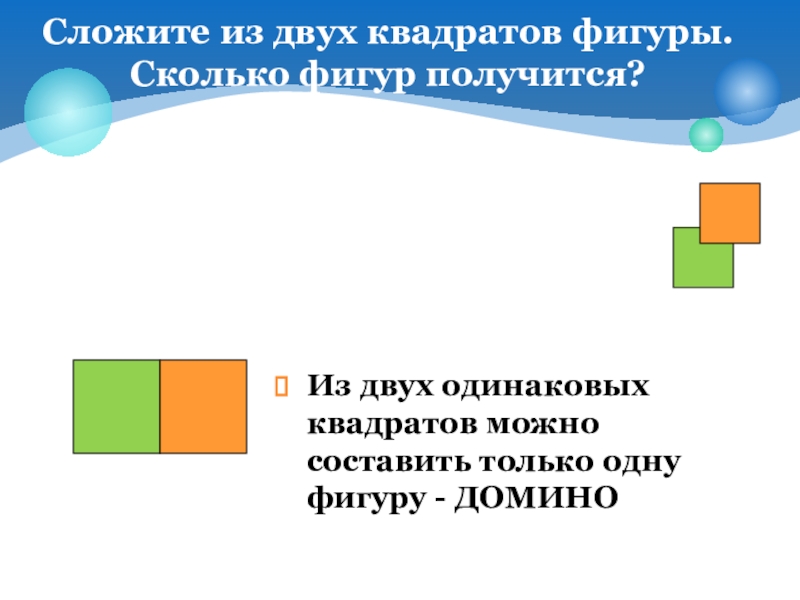
- 18. Сложите из двух квадратов фигуры. Сколько фигур
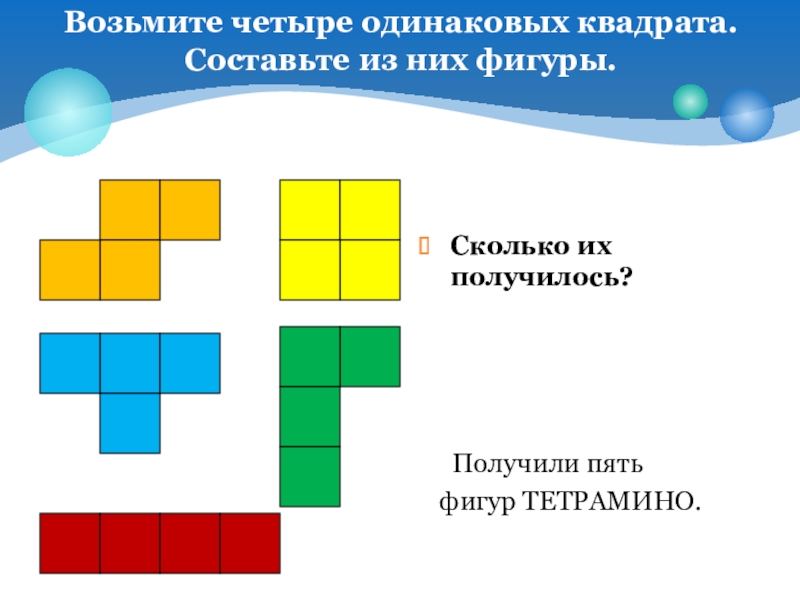
- 19. Составьте из них фигуры.
- 20. Получили пять фигур
- 21. Задача Составьте из пяти квадратов все возможные фигуры. Сколько их получилось?
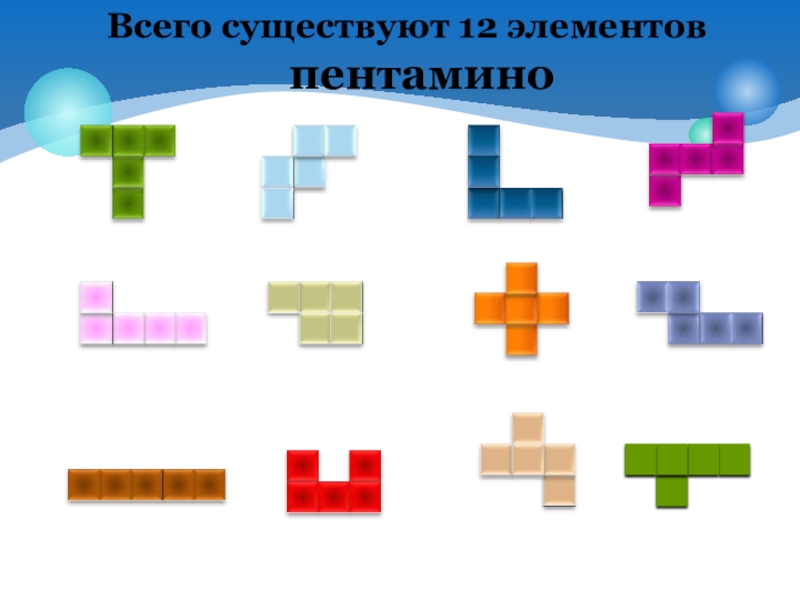
- 22. Всего существуют 12 элементов пентамино
- 23. Можно уложить все 12 фигур пентамино в
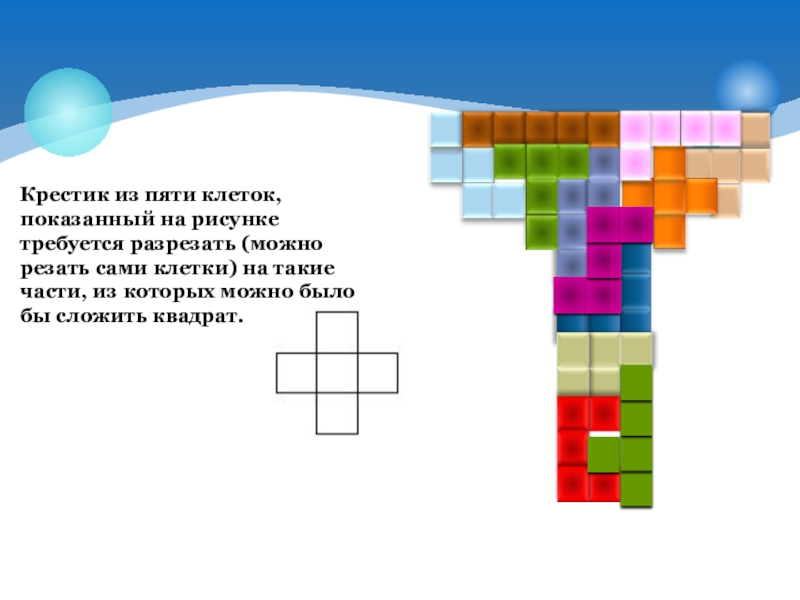
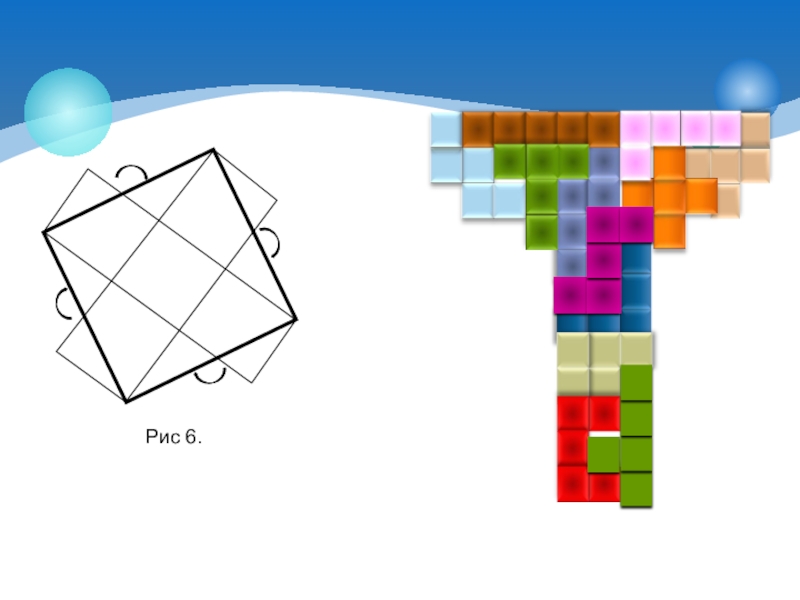
- 24. Крестик из пяти клеток, показанный на рисунке
- 25. Слайд 25
- 26. Спасибо за внимание!
Слайд 2Искать решение задач на разрезание ученые начали еще с древнейших времен.
ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 3Местный торговец земельными участками
отхватил по случаю кусок земли необычной
формы (он
Но каждый, из восьми найденных
им покупателей, хотел иметь
участок не хуже, чем у соседа.
Где торговец должен установить
разделительные изгороди,
чтобы получилось 8
одинаковых участков?
Ответ
Слайд 5ИСТОРИЧЕСКАЯ СПРАВКА
Первые попытки к решению были разработаны древними греками, китайцами. Так,
Слайд 6Но систематизировать подход к решению задач на разрезание смог арабский математик,
Слайд 7Абу-л-Вафа
Иранский учёный
Википедия
Персидский учёный X века, один из крупнейших математиков и астрономов
Родился: 10 июня 940 г., Хорасан
Умер: 998 г. (58 лет), Багдад
Чем известен: тангенс, котангенс, теорема синусов
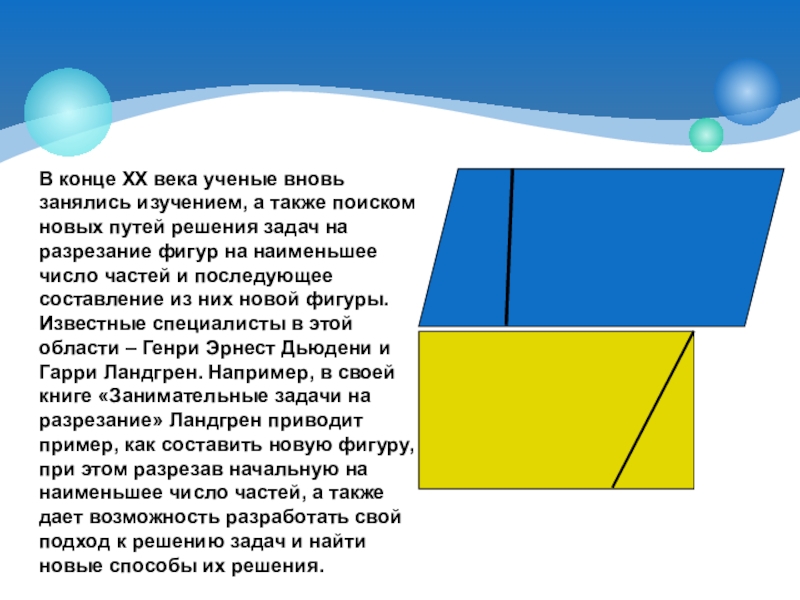
Слайд 8В конце XX века ученые вновь занялись изучением, а также поиском
Слайд 9Эта пословица предостерегает Вас от поспешности в решении задач.
Заданную фигуру, которая
Если эти части можно наложить одна на другую так, что они совпадут ( при этом разрешено фигуры переворачивать), то задача решена верно.
«Семь раз отмерь, один раз отрежь!»
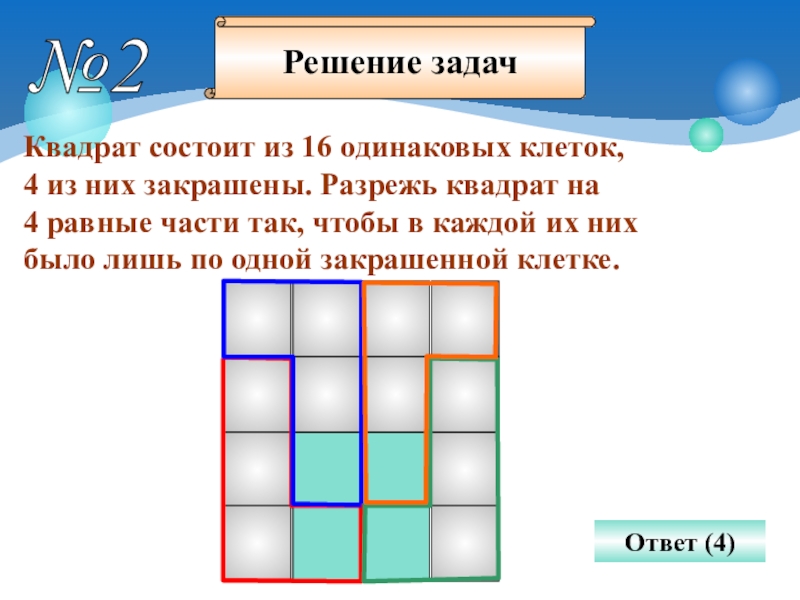
Слайд 10№2
Квадрат состоит из 16 одинаковых клеток,
4 из них закрашены. Разрежь
4 равные части так, чтобы в каждой их них
было лишь по одной закрашенной клетке.
Ответ (4)
Решение задач
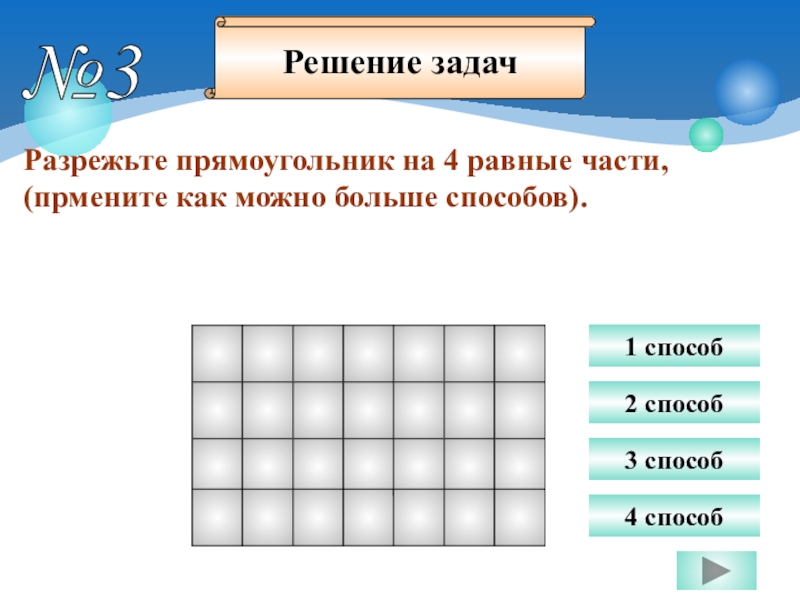
Слайд 11№3
Разрежьте прямоугольник на 4 равные части,
(прмените как можно больше
1 способ
Решение задач
2 способ
3 способ
4 способ
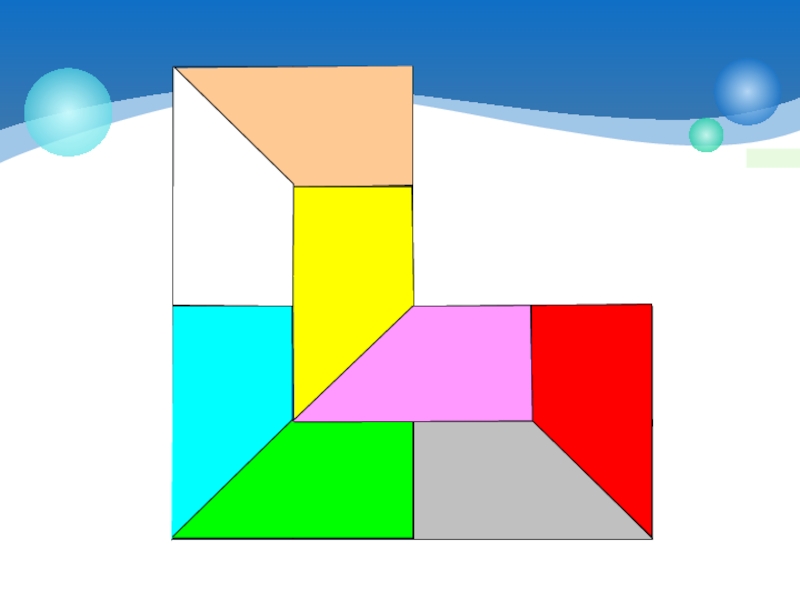
Слайд 16 Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме
Разрежьте данную фигуру на 5 равных по форме частей:
Задача усложняется: нужно фигуру разрезать на 4 разных по форме фигурки (не обязательно на прямоугольники).
Разрежьте эту фигуру на 5 фигур из четырех клеток разной формы таким образом, чтобы в каждой их них была закрашена только одна зеленая клетка.
Слайд 18Сложите из двух квадратов фигуры. Сколько фигур получится?
Из двух одинаковых квадратов
Слайд 19 Составьте из них фигуры. Сколько их получилось?
Возьмите три
Получившиеся
фигуры называют
ТРИМИНО.
Слайд 20
Получили пять
фигур ТЕТРАМИНО.
Сколько их получилось?
Возьмите четыре
Слайд 23Можно уложить все 12 фигур пентамино в прямоугольник 6*10. Фигурки можно
Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10.
Эту задачу впервые решил в 1965 году Джон Флетчер.
Задача.