«Живая геометрия –
геометрия природы»
Выполнила Марченко Ирина Николаевна
учитель математики
специалист высшей категории,
звание «Старший учитель»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Живая геометрия - геометрия природы
Содержание
- 1. Презентация по геометрии Живая геометрия - геометрия природы
- 2. Слайд 2
- 3. Природа — совершенное
- 4. Какую форму чаще всего
- 5. Симметрия в природе Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия
- 6. Осевая симметрия- симметрия относительно прямой
- 7. Зеркальная симметрия (отражение), когда объект при отражении переходит в себя
- 8. Винтовая симметрия В пространстве
- 9. Поворотная симметрия Многие цветы
- 10. Слайд 10
- 11. ФракталыФрактал – это математическое понятие многоканального и
- 12. побережья морей и берега рек
- 13. облака, кроны деревьев,
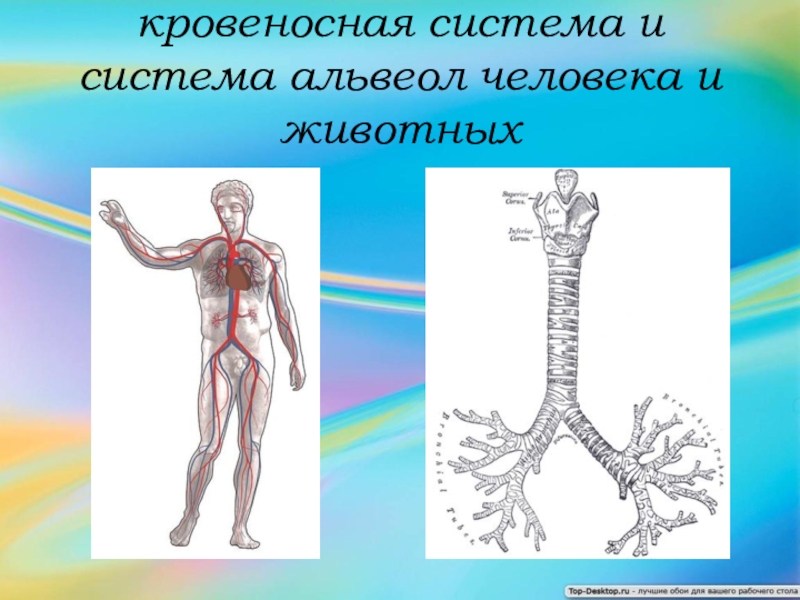
- 14. кровеносная система и система альвеол человека и животных
- 15. цветы и растения
- 16. Пропорции «золотого сечения» Ещё древние греки, а,
- 17. Пропорция
- 18. Да и в
- 19. Далёкие спиральные галлактики, которые засняли спут-ники, также закручиваются по спиралям Фибоначчи.
- 20. «Золотую пропорцию» можно увидеть и в строении
- 21. Для многих людей математика –
- 22. СПАСИБО ЗА ВНИМАНИЕ!
Окружающий нас мир – это мир геометрии
Слайд 3 Природа — совершенное творение, убеждаются учёные,
которые открывают в строении человеческо-го тела пропорции золотого сечения, а в головке цвет-ной капусты — фрактальные фигуры.
«Изучение и наблюдение природы породило науку»,- писал Цицерон в первом столетии до нашей эры. В бо-лее поздние времена с развитием науки и отдалением её от изучения природы, учёные с удивлением откры-вают то, что было известно ещё нашим предкам, но не было подтверждено научными методами.
Интересно находить схожие образования в мик-ро- и макромире, вдохновлять может и то, что гео-метрию этих образований наука может описать. Кровеносная система, река, молния, ветки деревьев… Всё это — схожие системы, состоящие из разных час-тиц и различные по масштабу.
«Изучение и наблюдение природы породило науку»,- писал Цицерон в первом столетии до нашей эры. В бо-лее поздние времена с развитием науки и отдалением её от изучения природы, учёные с удивлением откры-вают то, что было известно ещё нашим предкам, но не было подтверждено научными методами.
Интересно находить схожие образования в мик-ро- и макромире, вдохновлять может и то, что гео-метрию этих образований наука может описать. Кровеносная система, река, молния, ветки деревьев… Всё это — схожие системы, состоящие из разных час-тиц и различные по масштабу.
Слайд 4 Какую форму чаще всего принимают тела в природе?
Посмотрев вокруг, мы увидим, что чаще всего это круг, дуга, сфера и шар.
Фигура, близкая к кругу, получится, если разрезать поперек арбуз или апельсин, дугу напоминает радуга, сферу – одуванчик, шар – крыжовник, смородина, ягоды рябины, свечка каштана напоминает конус..
Фигура, близкая к кругу, получится, если разрезать поперек арбуз или апельсин, дугу напоминает радуга, сферу – одуванчик, шар – крыжовник, смородина, ягоды рябины, свечка каштана напоминает конус..
Слайд 5Симметрия в природе
Внимательное наблюдение показывает, что основу красоты многих
форм, созданных природой, составляет симметрия
Слайд 8Винтовая симметрия
В пространстве существуют тела,обладающие винтовой симметрией, т.
е. совмещаю-щиеся со своим первона-чальным положением после поворота на угол вокруг оси, дополненного сдвигом вдоль
той же оси.
Винтовая симметрия наблюдается в расположении листьев на стеблях большин-ства растений.
той же оси.
Винтовая симметрия наблюдается в расположении листьев на стеблях большин-ства растений.
Слайд 9Поворотная симметрия
Многие цветы обладают характерным свойством: цветок
можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии.
Слайд 11Фракталы
Фрактал – это математическое понятие многоканального и многоуровневого подобия самому себе.
Многие
объекты в природе обладают фрактальными свойствами:
Слайд 16Пропорции «золотого сечения»
Ещё древние греки, а, возможно, и египтяне, знали пропорцию
«золотого сечения». Лука Пачоли, математик эпохи Возрождения, назвал это соотношение «божественной пропорцией». Позже учёные обнаружили, что золотое сечение, которое так приятно глазу человека и которое часто встречается в классической архитектуре, искусстве и даже поэзии, можно повсеместно найти и в природе.
Пропорция золотого сечения — это деление отрезка на две неравные части, в котором короткая часть так относится к длинной, как длинная ко всему отрезку.
Пропорция золотого сечения — это деление отрезка на две неравные части, в котором короткая часть так относится к длинной, как длинная ко всему отрезку.
Слайд 17 Пропорция золотого сечения воспринимается человеческим
глазом как красивая, гармоничная. А ещё пропорция 0,618… равняется отношению предыдущего к последующему числу в ряде Фибоначчи. Числа ряда Фибоначчи повсеместно проявляются в природе: это спираль, по которой веточки растений примыкают к стеблю, спираль, по которой вырастают чешуйки на шишке или зёрна на подсолнухе. Что интересно, количество рядов, закручивающихся против часовой стрелки и по часовой стрелке, — это соседние числа в ряде Фибоначчи.
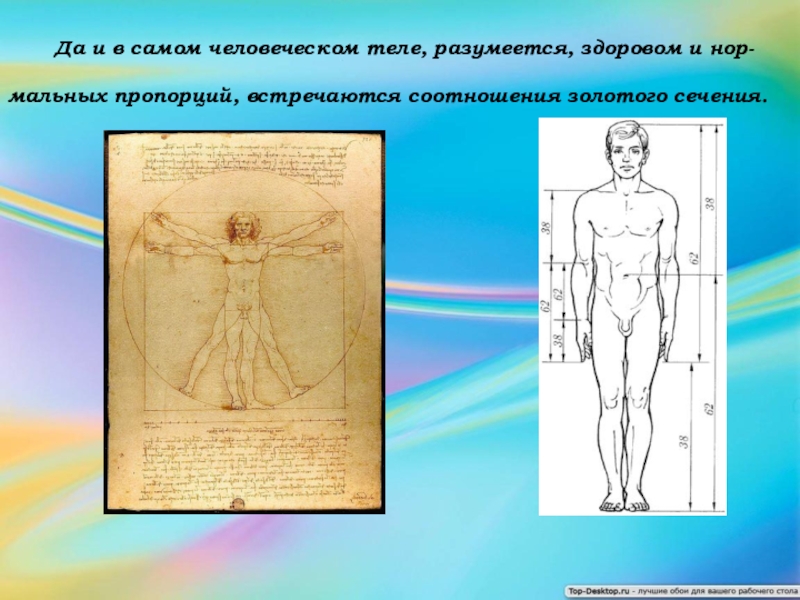
Слайд 18 Да и в самом человеческом теле, разумеется,
здоровом и нор-мальных пропорций, встречаются соотношения золотого сечения.
Слайд 19Далёкие спиральные галлактики, которые засняли спут-ники, также закручиваются по спиралям Фибоначчи.
Слайд 20«Золотую пропорцию» можно увидеть и в строении тела бабочки, в отношении
грудной и брюшной частей её тельца, а также у стрекозы.
Слайд 21 Для многих людей математика – скучная и сложная наука,
но математика – не только цифры, уравнения и решения, но и красота в строении геометрических тел и живых организмов.