ShareSlide^ru

Презентация, доклад по геометрии Свойства равнобедренного треугольника

Содержание

1. Презентация по геометрии Свойства равнобедренного треугольника
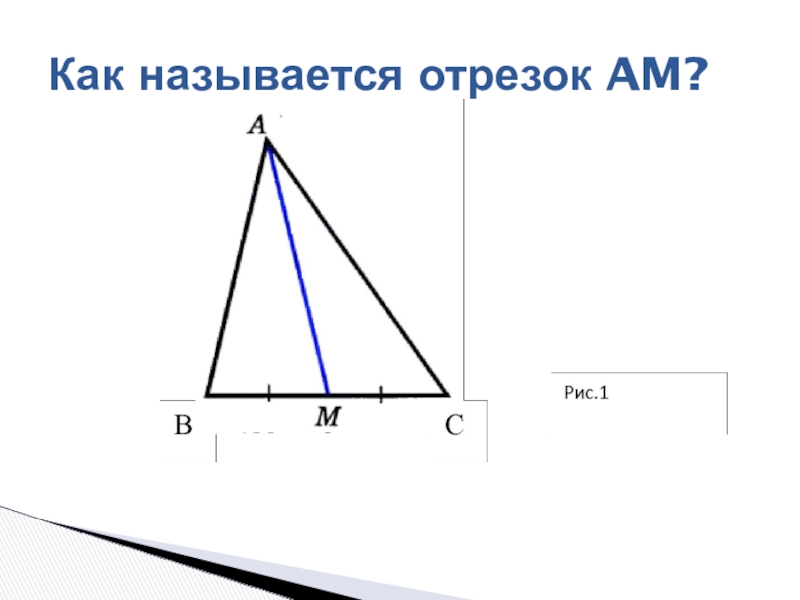
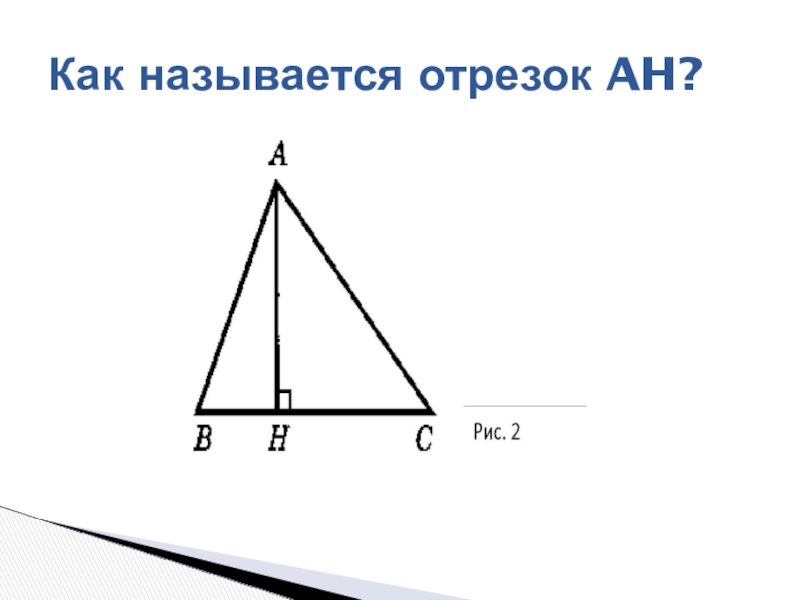
2. Как называется отрезок AH?
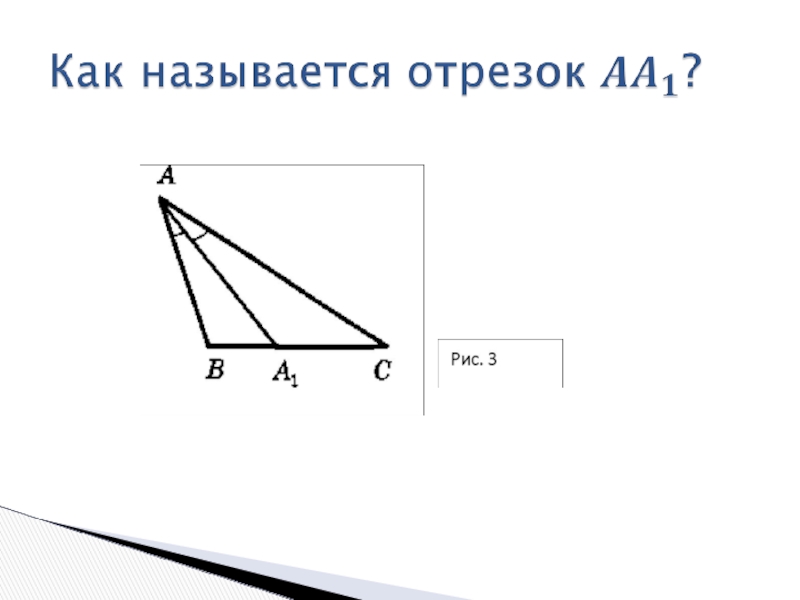
3.
4. «Равнобедренный треугольник и его свойства»Тема урока:
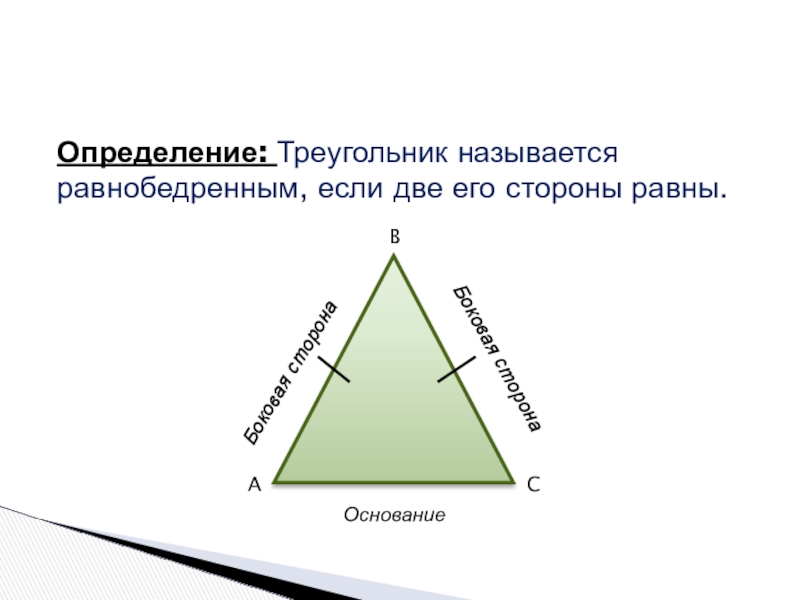
5. Определение: Треугольник называется равнобедренным, если две его стороны равны.ABCБоковая сторонаБоковая сторонаОснование
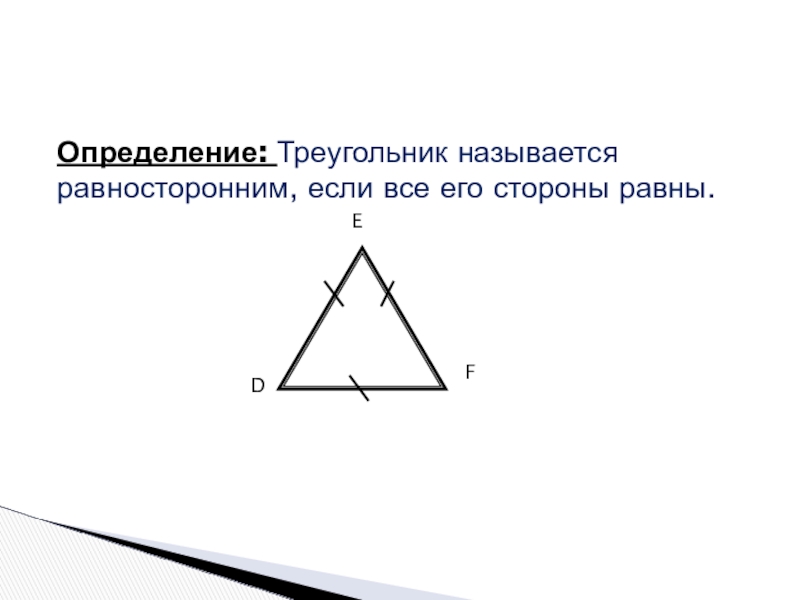
6. Определение: Треугольник называется равносторонним, если все его стороны равны.DEF
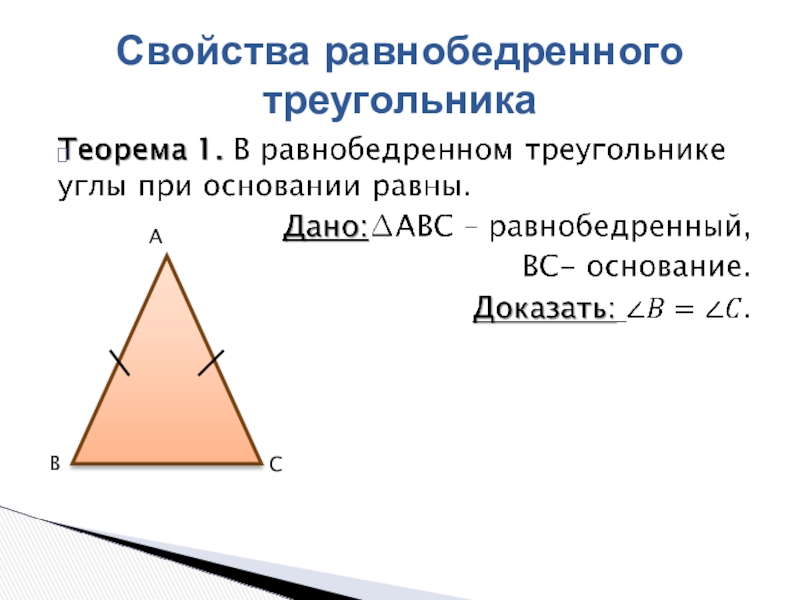
7. Свойства равнобедренного треугольникаBAC
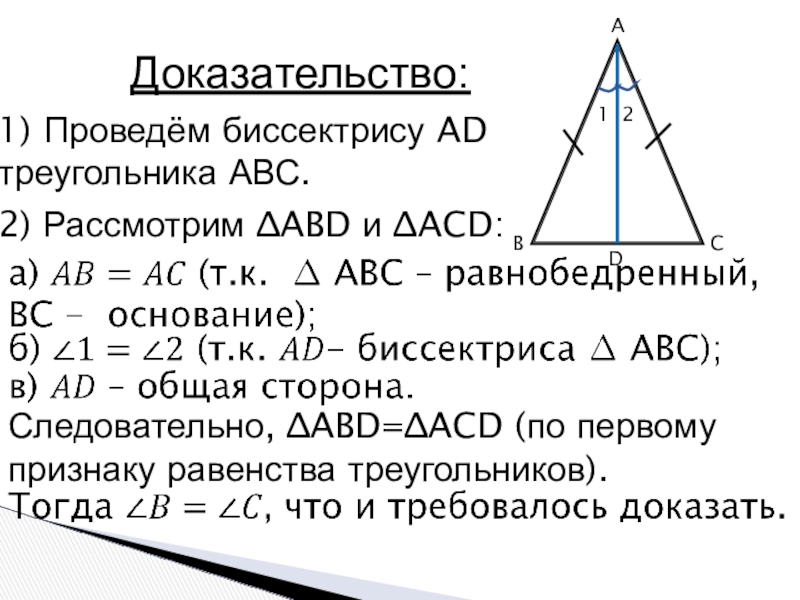
8. ABCDДоказательство:1) Проведём биссектрису AD треугольника АВС.2) Рассмотрим ∆ABD и ∆ACD: 12 Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).
9. Теорема 2. В равнобедренном треугольнике биссектриса, проведённая
10. Доказательство:1) Рассмотрим ∆ABD и ∆ACD: Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).
11. 1. Высота равнобедренного треугольника, проведённая к основанию,
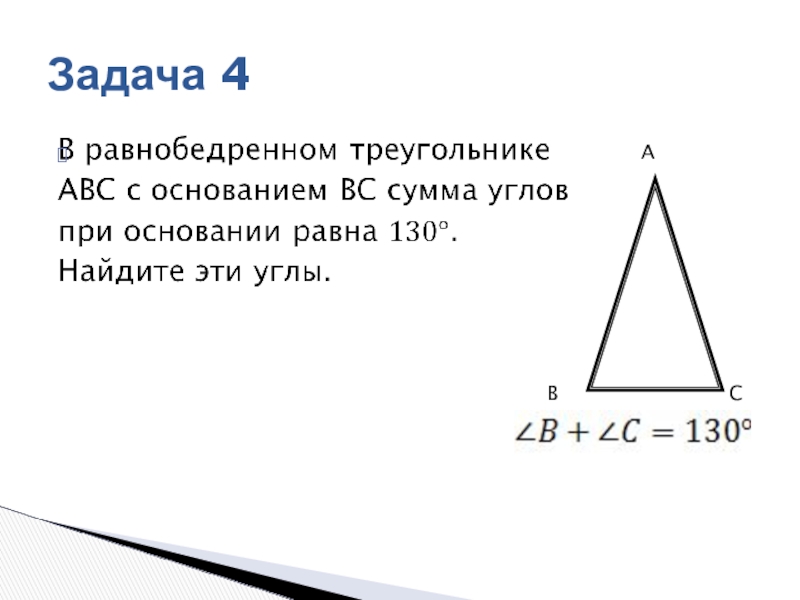
12. ABC Задача 4
13. В равнобедренном треугольнике ABC проведена биссектриса AD
14. Домашнее задание

Как называется отрезок AH?

Главная
Математика
Презентация по геометрии Свойства равнобедренного треугольника

Слайд 1Как называется отрезок AM?

Как называется отрезок AM?

Слайд 2Как называется отрезок AH?

Как называется отрезок AH?

Слайд 3

Слайд 4«Равнобедренный треугольник и его свойства»
Тема урока:

«Равнобедренный треугольник и его свойства»Тема урока:

Слайд 5Определение: Треугольник называется равнобедренным, если две его стороны равны.

A
B
C
Боковая сторона
Боковая сторона
Основание

Определение: Треугольник называется равнобедренным, если две его стороны равны.ABCБоковая сторонаБоковая сторонаОснование

Слайд 6Определение: Треугольник называется равносторонним, если все его стороны равны.

D
E
F

Определение: Треугольник называется равносторонним, если все его стороны равны.DEF

Слайд 7
Свойства равнобедренного треугольника

B
A
C

Свойства равнобедренного треугольникаBAC

Слайд 8
A
B
C

D

Доказательство:
1) Проведём биссектрису AD треугольника АВС.
2) Рассмотрим ∆ABD и ∆ACD:

1
2

Следовательно, ∆ABD=∆ACD

(по первому признаку равенства треугольников).

ABCDДоказательство:1) Проведём биссектрису AD треугольника АВС.2) Рассмотрим ∆ABD и ∆ACD: 12 Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).

Слайд 9Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой

и высотой.
Дано: ∆ ABC – равнобедренный,
ВС - основание,
AD-биссектриса.
Доказать:AD-медиана,
AD-высота.

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.Дано: ∆ ABC – равнобедренный,

Слайд 10Доказательство:
1) Рассмотрим ∆ABD и ∆ACD:

Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).

Доказательство:1) Рассмотрим ∆ABD и ∆ACD: Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).

Слайд 111. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
2.

Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.2. Медиана равнобедренного треугольника, проведённая к основанию,

Слайд 12
A
B
C

Задача 4

ABC Задача 4

Слайд 13В равнобедренном треугольнике ABC проведена биссектриса AD к основанию. Отрезок BD

равен 7 см. Найдите основание треугольника.

Задача 5

A

B

C

D

В равнобедренном треугольнике ABC проведена биссектриса AD к основанию. Отрезок BD равен 7 см. Найдите основание треугольника.Задача

Слайд 14Домашнее задание

Домашнее задание

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть