Презентация, доклад по геометрии Первый признак равенства треугольников

Содержание

1. Презентация по геометрии Первый признак равенства треугольников
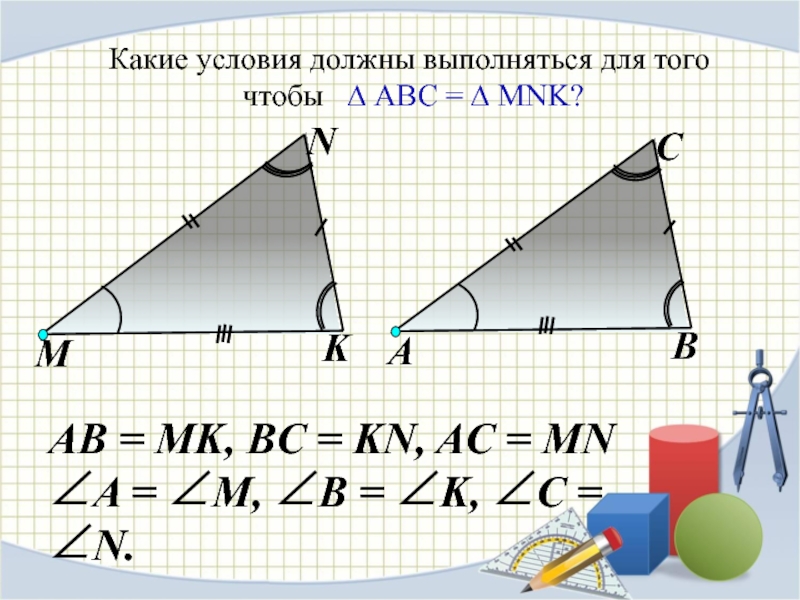
2. Какие условия должны выполняться для того чтобы
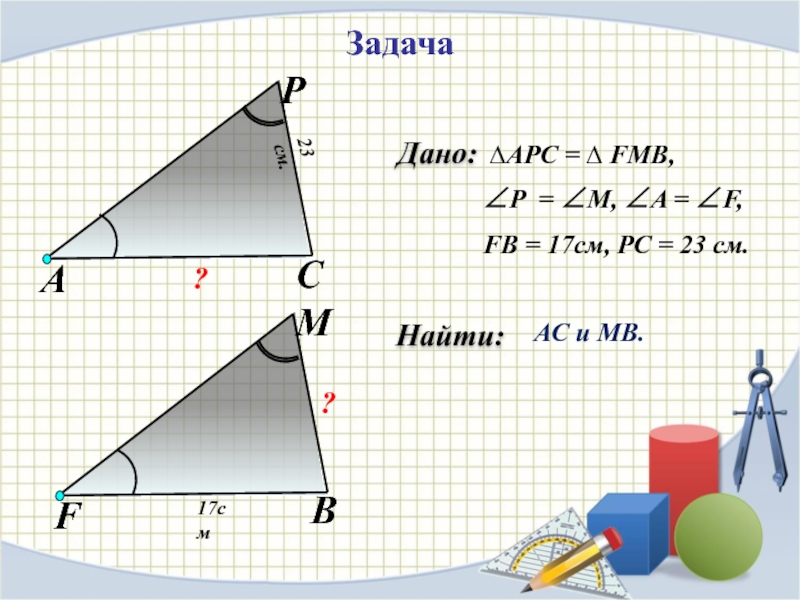
3. Найти:Задача ∆АPC = ∆ FMB, ∠P =
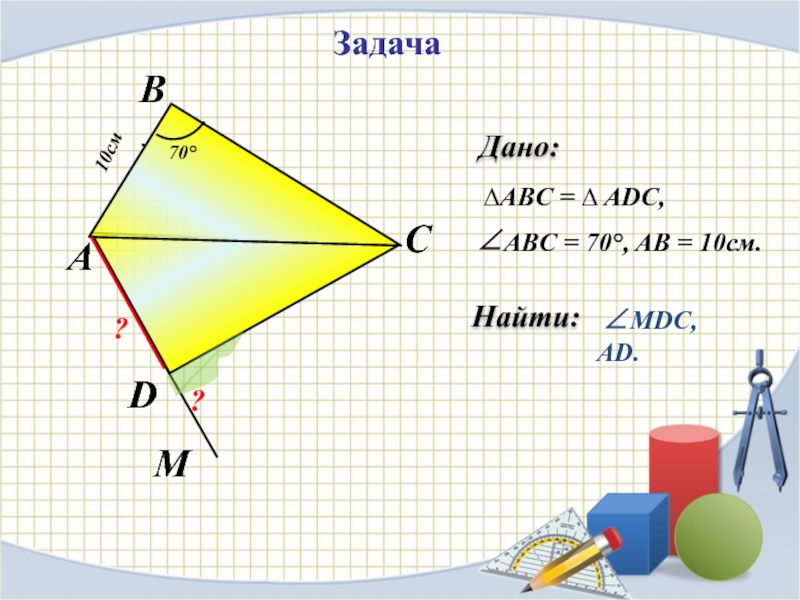
4. ЗадачаНайти: ∆АВC = ∆ ADC, ∠ABC = 70°, AB = 10см. ∠MDC, AD.АDCBM??10см.70°Дано:
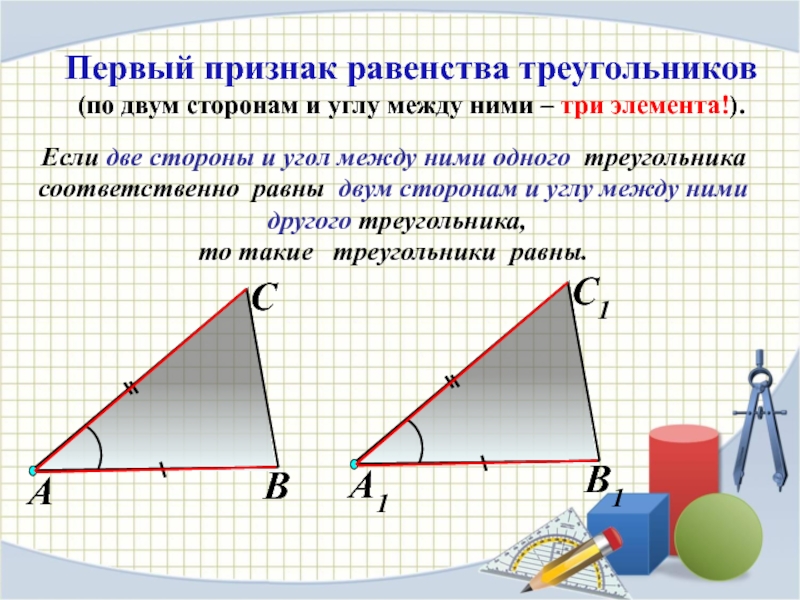
5. Первый признак равенства треугольников(по двум сторонам и
6. Теорема:Доказать:(условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁,
7. Два треугольника называются равными, если при наложении
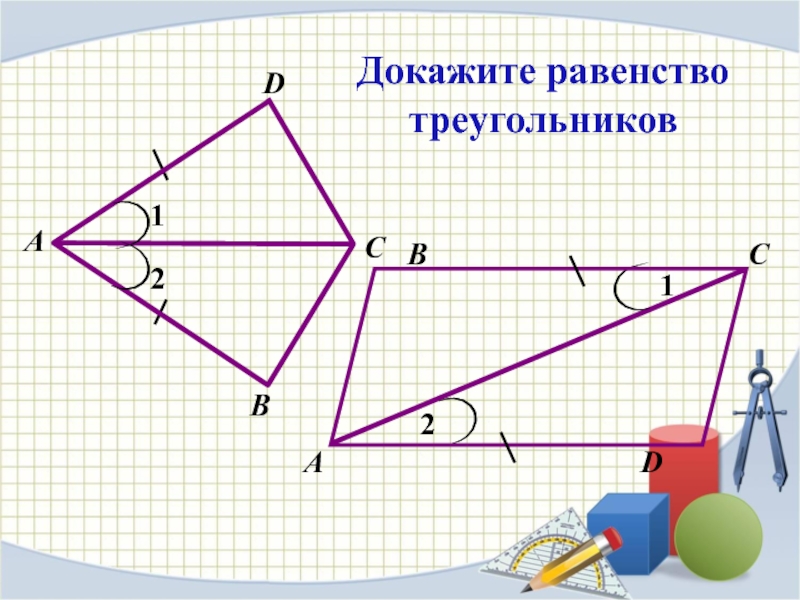
8. ВАС12DВАСD12Докажите равенство треугольников
9. ЗадачаОтрезки АЕ и DC пересекаются в точке
10. Домашнее заданиеп.15 № 92, 93
11. Источник шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. ИвановоСайт: http://pedsovet.su/

Какие условия должны выполняться для того чтобы ∆ АВС = ∆ MNK? АВ = MK, BС = KN, AC = MN∠A = ∠M, ∠B = ∠K, ∠C = ∠N.

Главная
Математика
Презентация по геометрии Первый признак равенства треугольников

Слайд 1Первый признак равенства треугольников
Медведева Елизавета Владимировна
учитель математики
МОУ СОШ № 25

г. Сочи

Слайд 2Какие условия должны выполняться для того
чтобы ∆ АВС

= ∆ MNK?

АВ = MK, BС = KN, AC = MN
∠A = ∠M, ∠B = ∠K, ∠C = ∠N.

Какие условия должны выполняться для того чтобы ∆ АВС = ∆ MNK? АВ = MK, BС

Слайд 3Найти:
Задача
∆АPC = ∆ FMB,
∠P = ∠M, ∠A = ∠F,

FB = 17см, PC = 23 см.

АС и МВ.

Дано:

Найти:Задача ∆АPC = ∆ FMB, ∠P = ∠M, ∠A = ∠F, FB = 17см, PC = 23

Слайд 4Задача
Найти:
∆АВC = ∆ ADC,
∠ABC = 70°, AB = 10см.

∠MDC, AD.

10см.

70°

Дано:

Слайд 5Первый признак равенства треугольников
(по двум сторонам и углу между ними –

три элемента!).

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними
другого треугольника,
то такие треугольники равны.

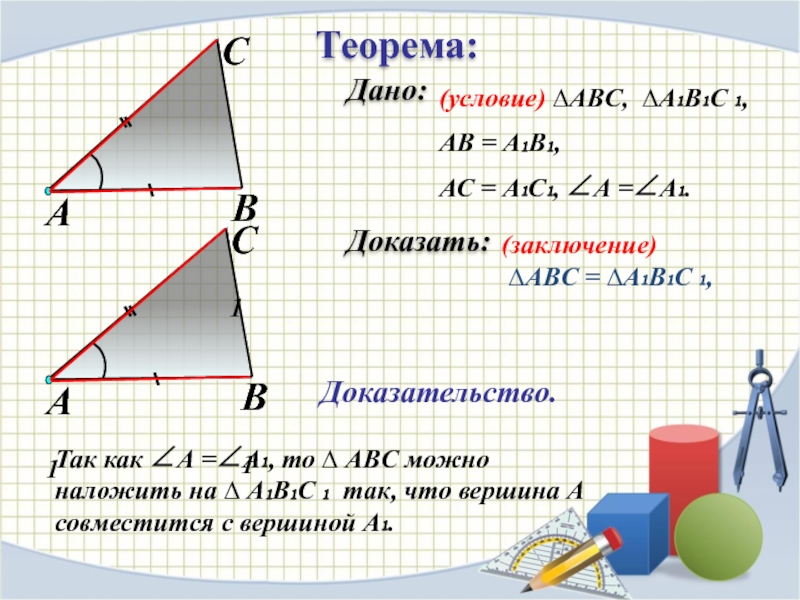
Слайд 6Теорема:
Доказать:
(условие) ∆АВC, ∆А₁В₁С ₁,
АВ = А₁В₁,
АС = А₁С₁, ∠А

=∠А₁.

(заключение)
∆АВC = ∆А₁В₁С ₁,

Доказательство.

Так как ∠А =∠А₁, то ∆ АВC можно наложить на ∆ А₁В₁С ₁ так, что вершина А совместится с вершиной А₁.

Дано:

Теорема:Доказать:(условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁, АС = А₁С₁, ∠А =∠А₁. (заключение) ∆АВC = ∆А₁В₁С ₁,

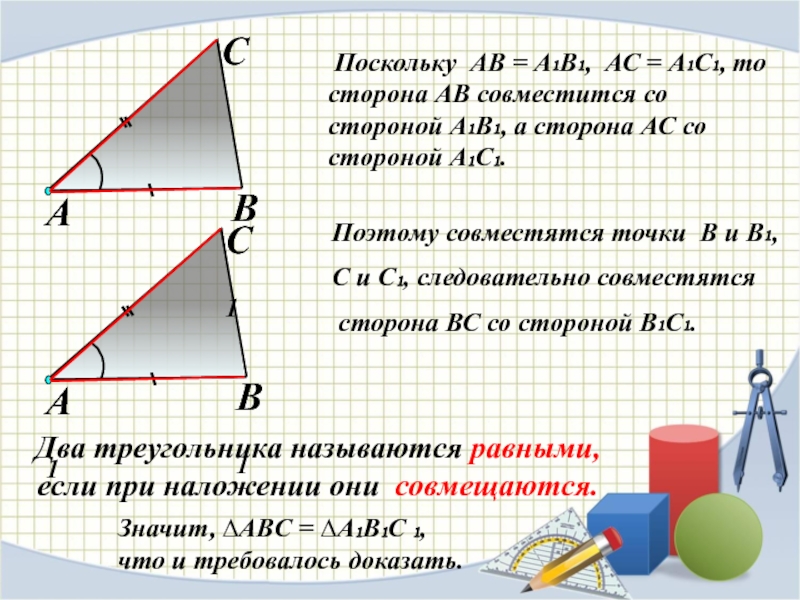
Слайд 7Два треугольника называются равными, если при наложении они совмещаются.

Поскольку АВ = А₁В₁, АС = А₁С₁, то сторона АВ совместится со стороной А₁В₁, а сторона АС со стороной А₁С₁.

Поэтому совместятся точки В и В₁,
С и С₁, следовательно совместятся
сторона ВС со стороной В₁С₁.

Значит, ∆АВC = ∆А₁В₁С ₁,
что и требовалось доказать.

Два треугольника называются равными, если при наложении они совмещаются. Поскольку АВ = А₁В₁, АС

Слайд 8В
А
С

1
2

D
В
А
С

D
1
2

Докажите равенство треугольников

Слайд 9
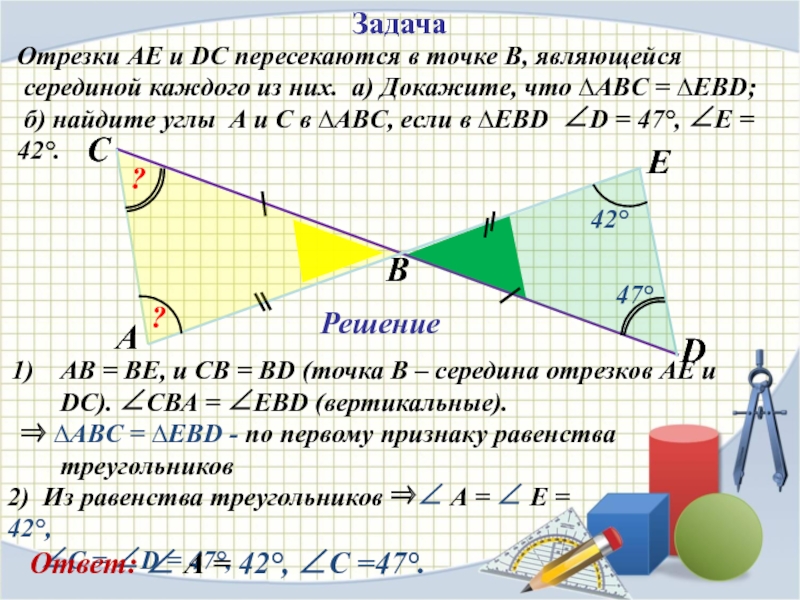
Задача
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой

каждого из них. а) Докажите, что ∆АВC = ∆ЕВD;
б) найдите углы А и С в ∆АВC, если в ∆ЕВD ∠D = 47°, ∠E = 42°.

Решение

42°

47°

АВ = ВЕ, и СВ = ВD (точка В – середина отрезков АЕ и DC). ∠СВА = ∠ЕВD (вертикальные).
⇒ ∆АВC = ∆ЕВD - по первому признаку равенства треугольников

2) Из равенства треугольников ⇒∠ А = ∠ Е = 42°,
∠С = ∠D = 47°,

Ответ: ∠ А = 42°, ∠С =47°.

ЗадачаОтрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. а) Докажите, что ∆АВC

Слайд 10Домашнее задание
п.15 № 92, 93

Слайд 11
Источник шаблона:

Ранько Елена Алексеевна
учитель начальных классов
МАОУ лицей №21

г. Иваново

Сайт: http://pedsovet.su/

Скачать презентацию

Презентация, доклад по геометрии Первый признак равенства треугольников

Содержание

Слайд 1Первый признак равенства треугольников
Медведева Елизавета Владимировна
учитель математики
МОУ СОШ № 25

Слайд 2Какие условия должны выполняться для того
чтобы ∆ АВС

Слайд 3Найти:
Задача
∆АPC = ∆ FMB,
∠P = ∠M, ∠A = ∠F,

Слайд 4Задача
Найти:
∆АВC = ∆ ADC,
∠ABC = 70°, AB = 10см.

Слайд 5Первый признак равенства треугольников
(по двум сторонам и углу между ними –

Слайд 6Теорема:
Доказать:
(условие) ∆АВC, ∆А₁В₁С ₁,
АВ = А₁В₁,
АС = А₁С₁, ∠А

Слайд 7Два треугольника называются равными, если при наложении они совмещаются.

Слайд 8В
А
С

1
2

D
В
А
С

D
1
2

Докажите равенство треугольников

Слайд 9
Задача
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой

Слайд 10Домашнее задание
п.15 № 92, 93

Слайд 11
Источник шаблона:

Ранько Елена Алексеевна
учитель начальных классов
МАОУ лицей №21

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по геометрии Первый признак равенства треугольников

Содержание

Слайд 1Первый признак равенства треугольников Медведева Елизавета Владимировнаучитель математики МОУ СОШ № 25

Слайд 2Какие условия должны выполняться для того чтобы ∆ АВС

Слайд 3Найти:Задача ∆АPC = ∆ FMB, ∠P = ∠M, ∠A = ∠F,

Слайд 4ЗадачаНайти: ∆АВC = ∆ ADC, ∠ABC = 70°, AB = 10см.

Слайд 5Первый признак равенства треугольников(по двум сторонам и углу между ними –

Слайд 6Теорема:Доказать:(условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁, АС = А₁С₁, ∠А

Слайд 7Два треугольника называются равными, если при наложении они совмещаются.

Слайд 8ВАС12DВАСD12Докажите равенство треугольников

Слайд 9ЗадачаОтрезки АЕ и DC пересекаются в точке В, являющейся серединой

Слайд 10Домашнее заданиеп.15 № 92, 93

Слайд 11Источник шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Первый признак равенства треугольников
Медведева Елизавета Владимировна
учитель математики
МОУ СОШ № 25

Слайд 2Какие условия должны выполняться для того
чтобы ∆ АВС

Слайд 3Найти:
Задача
∆АPC = ∆ FMB,
∠P = ∠M, ∠A = ∠F,

Слайд 4Задача
Найти:
∆АВC = ∆ ADC,
∠ABC = 70°, AB = 10см.

Слайд 5Первый признак равенства треугольников
(по двум сторонам и углу между ними –

Слайд 6Теорема:
Доказать:
(условие) ∆АВC, ∆А₁В₁С ₁,
АВ = А₁В₁,
АС = А₁С₁, ∠А

Слайд 8В
А
С

1
2

D
В
А
С

D
1
2

Докажите равенство треугольников

Слайд 9
Задача
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой

Слайд 10Домашнее задание
п.15 № 92, 93

Слайд 11
Источник шаблона:

Ранько Елена Алексеевна
учитель начальных классов
МАОУ лицей №21