- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Взаимное расположение прямых в пространстве
Содержание
- 1. Презентация по геометрии на тему Взаимное расположение прямых в пространстве
- 2. Задача № 22Точки А и B лежат
- 3. AαMNBCДано:плоскость αAαBαCαAM=MCBN=NCaMaNaЗадача № 22Точки А и B
- 4. Задача № 25 Докажите, что если данная
- 5. Задача № 27Точка C лежит на отрезке
- 6. Взаимное расположение прямых на плоскости
- 7. Скрещивающиеся прямыеДве прямые называются скрещивающимися, если они не лежат в одной плоскостиMαab
- 8. Признак скрещивающихся прямыхТеорема: Если одна из двух
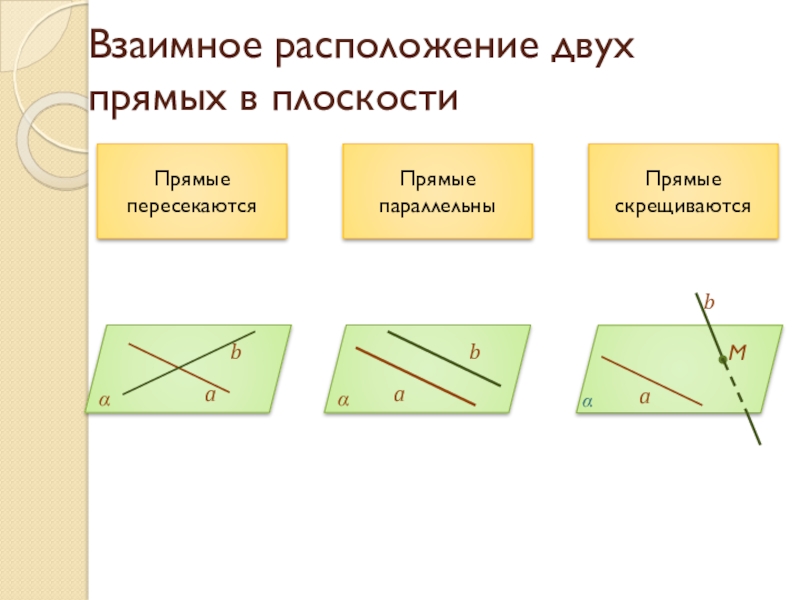
- 9. Взаимное расположение двух прямых в плоскостиПрямые пересекаютсяПрямые параллельныПрямые скрещиваютсяaαMαbbaaαb
- 10. Признак скрещивающихся прямыхТеорема: Через каждую из двух
- 11. Задача № 34Точка D не лежит в
Слайд 1Взаимное расположение прямых в пространстве
Разработала: Иванова М.В.
Преподаватель ГБОУ АО СПО АГПК
Слайд 2Задача № 22
Точки А и B лежат в плоскости α, а
Слайд 3A
α
M
N
B
C
Дано:
плоскость α
Aα
Bα
Cα
AM=MC
BN=NC
a
Ma
Na
Задача № 22
Точки А и B лежат в плоскости α,
Доказать:
a || α
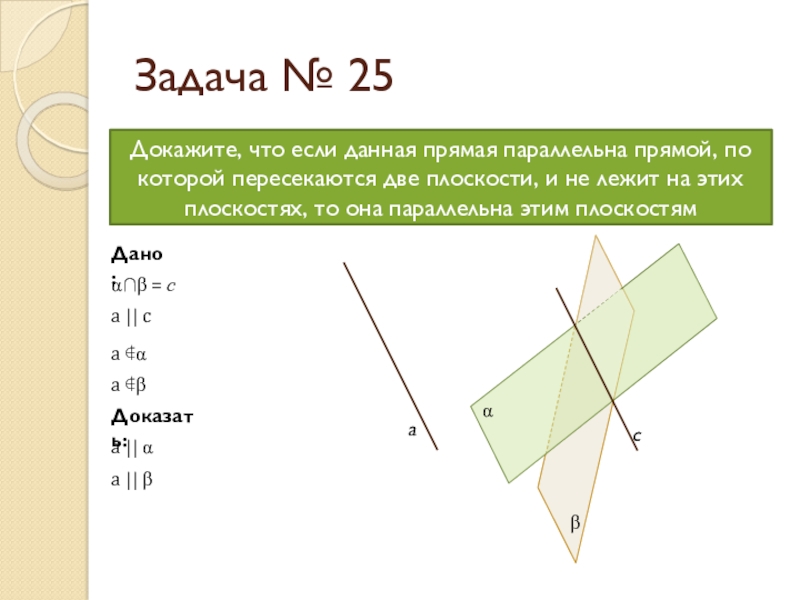
Слайд 4Задача № 25
Докажите, что если данная прямая параллельна прямой, по
Дано:
αβ = с
с
α
β
a || c
a
a ∉α
a ∉β
Доказать:
a || α
a || β
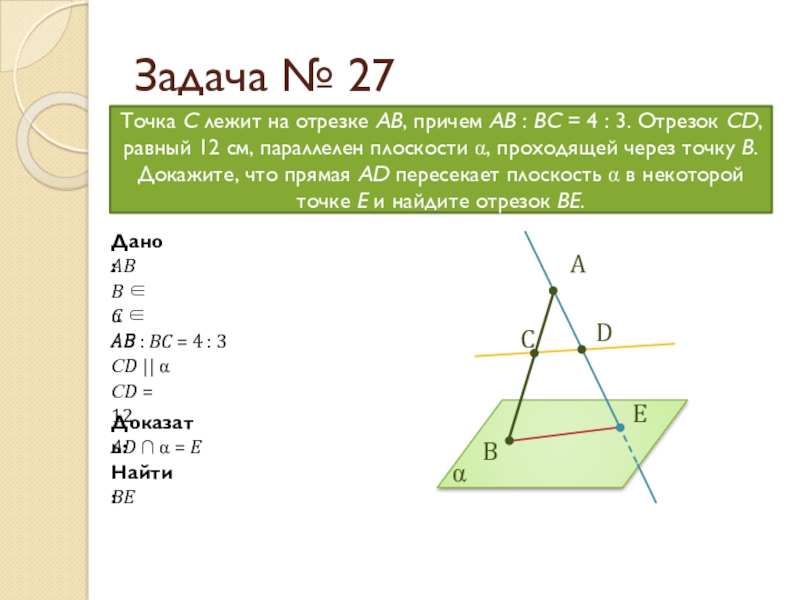
Слайд 5Задача № 27
Точка C лежит на отрезке AB, причем AB :
Дано:
AB
B ∈ α
C ∈ AB
AB : BC = 4 : 3
СD || α
СD = 12
Доказать:
AD α = E
Найти:
BE
α
B
A
C
D
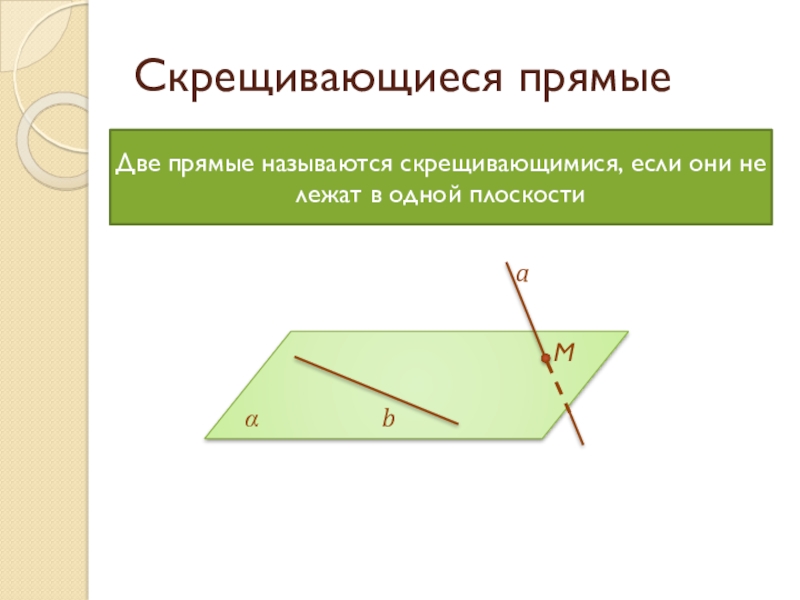
Слайд 7Скрещивающиеся прямые
Две прямые называются скрещивающимися, если они не лежат в одной
M
α
a
b
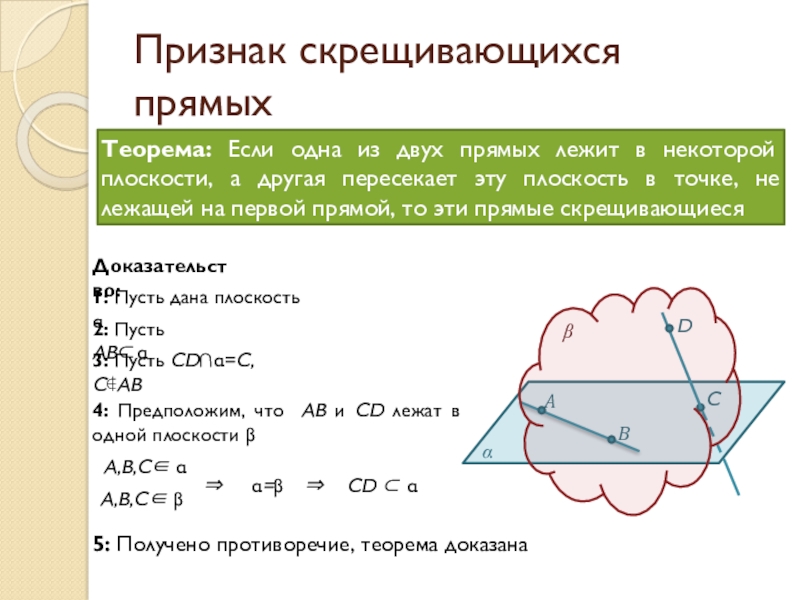
Слайд 8Признак скрещивающихся прямых
Теорема: Если одна из двух прямых лежит в некоторой
C
α
B
Доказательство:
A
D
1: Пусть дана плоскость α
2: Пусть ABα
3: Пусть CDα=C, CAB
4: Предположим, что AB и CD лежат в одной плоскости β
A,B,C α
A,B,C β
α=β
CD α
5: Получено противоречие, теорема доказана
Слайд 9Взаимное расположение двух прямых в плоскости
Прямые пересекаются
Прямые параллельны
Прямые скрещиваются
a
α
M
α
b
b
a
a
α
b
Слайд 10Признак скрещивающихся прямых
Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость,
Доказательство:
1: Даны скрещивающиеся прямые AB и CD
2: Проведем через точку А прямую AE||CD
3: Через две пересекающиеся прямые AB и AE можно провести плоскость (теорема)
4: Тогда
AE α
AE||CD
CD||α
II: Единственность
C
D
A
B
E
α
I . Существование
5: Пусть существует другая плоскость β такая, что:
AB β
β||CD
Тогда
βAE
βCD
Слайд 11Задача № 34
Точка D не лежит в плоскости треугольника ABC, точки
а) ND и AB; б) PK и BC ; в) MN и AB ; г) MP и AC ; д) KN и AC ; е) MD и BC ;
A
B
C
D
M
N
P
K
Решение:
а: ND и AB
ND ∩ AB=B
б: PK и BC
PK∩ BC=L
L
в: MN и AB
MN || AB
г: MP и AC
MP || AC
д: KN и AC
KN и AC скрещиваются
е: MD и BC
MD и BC скрещиваются